图像处理（四）：泊松图像融合
图像处理（四）：泊松图像融合
概念引入
首先从一个简单的一维插值问题开始研究。给出一维信号t和掩膜M，掩膜M为0的地方代表此处的“像素”是缺失的。
信号如图：
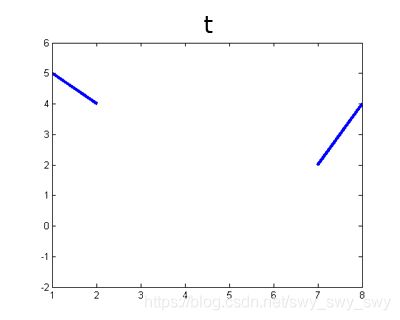
t = [5 4 0 0 0 0 2 4];
M = [0 0 1 1 1 1 0 0];
M = logical(M);
空白像素填充
我们可以把该插值问题转化为一下公式
此处的i代表掩膜下每一个像素的坐标。每一个j都是i的邻居像素，两个求和操作都会让像素在各个方向上的梯度尽量的趋近于0.
在左边第一个求和部分，我们计算的是两个未知像素的梯度，而右边求和部分则负责处理边界的情况，也就是有一个像素已知，一个像素未知。
在一维的情况下，我们定义“邻居”像素是在某像素左边的像素。那么这个最小二乘问题的解满足以下关系：
v(1) - t(2) = 0; %left border
v(2) - v(1) = 0;
v(3) - v(2) = 0;
v(4) - v(3) = 0;
t(7) - v(4) = 0; %right border
把已知的t值代入我们有
v(1) - 4 = 0;
v(2) - v(1) = 0;
v(3) - v(2) = 0;
v(4) - v(3) = 0;
2 - v(4) = 0;
我们把它转换为矩阵求解
A = [ 1 0 0 0; ...
-1 1 0 0; ...
0 -1 1 0; ...
0 0 -1 1; ...
0 0 0 -1];
b = [4; 0; 0; 0; -2];
像素融合
此处我们对插值的像素值引入约束条件：我们需要新填充像素的梯度尽可能的与s里的像素梯度相似。
s = [5 6 7 2 4 5 7 3];
对应的目标函数变为：
该问题的最小二乘解满足以下关系：
v(1) - t(2) = s(3) - s(2);
v(2) - v(1) = s(4) - s(3);
v(3) - v(2) = s(5) - s(4);
v(4) - v(3) = s(6) - s(5);
t(7) - v(4) = s(7) - s(6);
代入t和s的已知元素值，我们有
v(1) - 4 = 1;
v(2) - v(1) = -5;
v(3) - v(2) = 2;
v(4) - v(3) = 1;
2 - v(4) = 2;
我们把问题转换为矩阵形式求解，最后我们可以得到一个与s很相似的关于t的插值
A = [ 1 0 0 0; ...
-1 1 0 0; ...
0 -1 1 0; ...
0 0 -1 1; ...
0 0 0 -1];
b = [5; -5; 2; 1; 0];
一维融合
以下代码即可实现上面的融合
%matplotlib inline
from pylab import *
import numpy as np
from pprint import pprint
t = np.array([5., 4., 0., 0., 0., 0., 2., 4.])
mask = np.array([1, 1, 0, 0, 0, 0, 1, 1])
s = np.array([5., 6., 7., 2., 4., 5., 7., 3.]);
## EXAMPLE FOR 1D Possion Filling
mSize=np.count_nonzero(mask)
size=len(t)-mSize
A=np.eye(size + 1, size) - np.eye(size + 1, size, k = -1)
b=zeros(size+1)
offset=1
b[0]+=t[offset]
b[-1]-=t[offset+mSize+1]
pprint(A)
pprint(b)
lin=np.linalg.lstsq(A,b,rcond=None)
poisson=t
poisson[offset+1:offset+mSize+1] = lin[0]
pprint(poisson)
b2= zeros(size + 1)
for i in range(size + 1):
b2[i] = s[i+offset+1] - s[i+offset]
b2[0] += t[offset]
b2[-1] -= t[offset + mSize +1]
pprint(b2)
gr= np.linalg.lstsq(A, b2, rcond = None)
gradient = t
gradient[offset + 1 : offset + mSize + 1] = gr[0]
pprint(gradient)
plot(gradient)