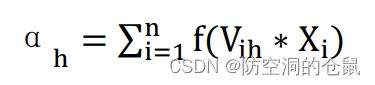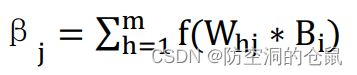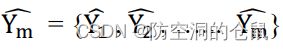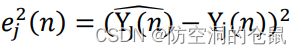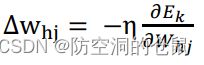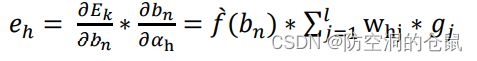多层感知机详细讲解(附代码)

1.1 单层感知机原理

        神经网络中，每一个神经元都具备多个权值参数 W 以及一个激活函数 f(X)和偏置 b , 输出值 Y 满足公式。 Y = f(∑ W୧ ୧ ଵ ∗ X୧ + b) （1) 其中 X 为输入值，W 为对应 X 的权重向量，b 为偏置，Y 期望响应，通常处理中将偏置 b 作为 W 中的一个值，增加一个对应的模拟输入 X，来简化运算。单个神经元结构,通过对一组数据来学习 其中的参数 W 以及 b 来进行拟合输出结果 Y。其结构如图 1 所示。 图 1 神经元结构图 之后通过计算期望响应和实际响应的误差来不断地对参数 W 和 b 进行调整，从而起到学习的效果。

1.2 多层感知机的原理

1.2.1 多层感知机网络结构

相较于单层感知机，多层感知机的改进如下：

1. 引入了隐藏层(hidden layer)的结构，隐藏层通常指代的是，输入层(input layer)和输出层(output layer)中间的具有 N 个神经元的结构。其中层与层之间采用全连接的结构，跨层之前没有相连。

2. 引入了新的非线性激活函数。

3. 采用了反向传播算法(back propagation)。

多层感知机的训练过程包括两个步骤：

1：前向传播：前向传播过程中，已知网络结构中的权重 W 的值和激活函数的类型，通过将其数 据输入给输入层，使得输入信号在网络结构中一层一层的传播，之后通过最后输出层得到一个输出结 果 Y，该 Y 值作为前向传播最终输出的结果，称之为期望响应。

2：反向传播：是通过比较网络的期望响应和实际响应之间的误差信号，通过将其误差信号回传到 模型的各个层中，考虑到误差信号只在输出层，而隐藏层没有与误差信号直接相连，因此更新参数的 过程中是通过链式求导的法则来对模型中的各个参数进行修正。 相较于单层感知机而言，多层感知机因为引入了更多的神经元，使得网络能够更好的拟合大量数据， 2 并且引入了非线性激活函数，使得网络具有了能够拟合非线性数据的能力。

多层感知机网络结构如下图 2 所示。

 1.2.2 前向传播过程

        假设给定数据集为 Xn = {(x1 ,y1), (x2 ,y2)…… (xn ,yn)}，其中 xi 为 n 维向量, yi 为 m 为向量，因 此输入为 n 个维度的变量，输出对应为 m 个维度的向量，因此多层感知机可以设置为:n 个输入神经 元、k 个隐层神经元(k 的个数不定)、m 个输出层神经元组层的网络结构。其中假设输出层第 i 个神经 元与隐层第 h 个神经元之间的权重为 Vih，隐层第 h 个神经元与输出层第 j 个神经元之间的权重为 Whj。

则隐层第 h 个神经元接收到的输入为:

  同时输出层第 j 个神经元接收到的输入为:( Bi)为第 h 个隐层神经元的输出

        之后通过前一层的输出连接到下一层的输入，从而实现了信号的传递，信号传递到最后一层的输 出，则为网络中的输出，这一个过程称之为信号的前向传播过程。

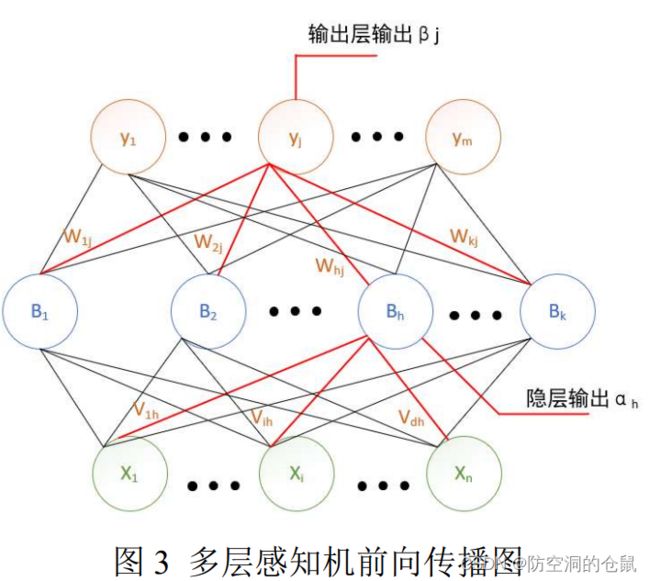
前向传播过程如下图 3 所示。

 1.2.3 反向传播过程

        反向传播算法(back propagation)，又称为 BP 算法。通过将误差信号反向传递回去，更新每一层权 重参数。

        定义输出响应为: 

        期望响应为

        此时定义误差函数为：

 其中为 Xn 第 j 个输出产生的误差信号，误差信号定义为：

         此时 BP 算法基于梯度下降(gradient descnet)方法，按照目标的负梯度方向对参数进行调整，因此 给定学习率 η，此时参数调整的公式为:

         由于隐层结构不与误差信号௝ ଶ()直接相连，因此采用链式求导的方式，来对隐层结构进行参数的 更新，具体公式为:

 

 同理:隐层参数的更新公式为:

 其中h的计算公式为:

 

         其中学习率η控制着算法每一次迭代中的更新步长，太大了容易震荡，并且不容易收敛到最优解， 太小了容易陷入局部最小值并且模型训练过慢,因此η数值的选取一般在 0-1 之间，并且合适的参数值， 要不断地试验.

#*******************************************************
import numpy as np
import csv
import matplotlib.pyplot as plt
import math
import random

#定义激活函数
def sigmoid(x):
    # return np.tanh(-2.0*x)
    return 1.0 / (1.0 + math.exp(-x))
def sigmoid_derivate(x):
    # return -2.0*(1.0-np.tanh(-2.0*x)*np.tanh(-2.0*x))
    return x * (1 - x)  # sigmoid函数的导数

def relu(x):
  return np.maximum(0.001*x,x)
def relu_derivate(x):
    if x <0 or x == 0 : return 0.001
    else :              return   

def tanh(x):
    return (math.exp(x)-math.exp(-x))/(math.exp(x)+math.exp(-x))
def tanh_derivate(x):
    return 1-(x*x)

class MLP(object):
    def __init__(self,lr,epoch,MLPSize):
      self.lr = lr
      self.epoch = epoch

      self.input_n = MLPSize[0] + 1
      self.hidden_n = MLPSize[1]
      self.output_n = MLPSize[2]

      self.input = self.input_n*[0.1]
      self.hidden = self.hidden_n*[0.1]
      self.output = self.output_n*[0.1]

      self.input_weights = np.random.normal(loc=0.0, scale=1.0, size=((self.input_n, self.hidden_n)))
      self.output_weights = np.random.normal(loc=0.0, scale=1.0, size=((self.hidden_n, self.output_n)))

    def predict(self, inputs):
        for i in range(self.input_n-1):
            self.input[i] = inputs[i]

        for j in range(self.hidden_n):
            total = 0
            for i in range(self.input_n):
                total += self.input[i] * self.input_weights[i][j]
            self.hidden[j] = relu(total)

        for k in range(self.output_n):
            total = 0
            for j in range(self.hidden_n):
                total += self.hidden[j] * self.output_weights[j][k] + self.bias_output[k]
            self.output[k] = relu(total)
        return self.output[:]

    def back_propagate(self, data, label):
        self.predict(data)
        output_deltas = [0.0] * self.output_n

        for o in range(self.output_n):
            error = label[o] - self.output[o]  
            output_deltas[o] = relu_derivate(self.output[o]) * error  

        hidden_deltas = [0.0] * self.hidden_n
        for j in range(self.hidden_n):
            error = 0
            for k in range(self.output_n):
                error += output_deltas[k] * self.output_weights[j][k]
            hidden_deltas[j] = relu_derivate(self.hidden[j]) * error

        for h in range(self.hidden_n):
            for o in range(self.output_n):
                change = output_deltas[o] * self.hidden[h]
                self.output_weights[h][o] += self.lr * change

        for i in range(self.input_n):
            for h in range(self.hidden_n):
                change = hidden_deltas[h] * self.input[i]
                self.input_weights[i][h] += self.lr * change
        error = 0
        for o in range(len(label)):
            for k in range(self.output_n):
                error += 0.5 * (label[o] - self.output[k]) ** 2
        return error

    def train(self, data, labels):
        loss = []
        epoch = []
        for i in range(self.epoch):
            error = 0
            for j in range(len(cases)):
                data = np.squeeze(data [j].tolist())
                label = labels[j]
                error += self.back_propagate(data, label)
            epoch.append(i)
            loss.append(error/len(data))
        return epoch,loss

    def fit(self):

        DataPath = r'.\Data\Data.csv'
        file = open(DataPath)
        reader = np.mat(list(csv.reader(file)),dtype=np.float64)
        epoch,loss = self.train(reader[:,:2], reader[:,2:3].tolist())  
        test_x = []
        test_y = []
        test_p = []

        yold = 0

        for x in np.arange(-15, 25, 0.1):
            for y in np.arange(-10, 10, 0.1):
                yp = self.predict(np.array([x, y]))
                if (yold < 0.5 and yp > 0.5):
                    test_x.append(x)
                    test_y.append(y)
				  yold = yp
         
        plt.figure(1)
        plt.title('MLP')
        plt.xlabel('value')
        plt.ylabel('value')
        plt.plot(test_x, test_y, 'b--')
        plt.plot(np.squeeze(reader[:,0:1].tolist()),
                 np.squeeze(reader[:,1:2].tolist()), 'r*')
        plt.savefig(r'.\Data' + '\\' + 'MLP1.png')
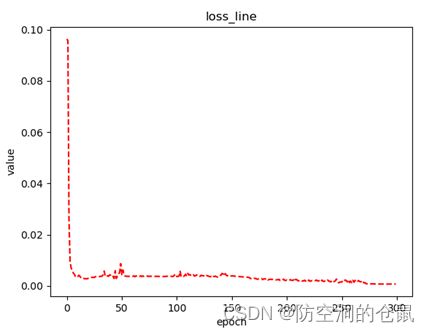
        plt.figure(2)
        plt.title('loss_line')
        plt.xlabel('epoch')
        plt.ylabel('value')
        plt.plot(epoch, loss, 'r--')
        plt.savefig(r'.\Data' + '\\' + 'MLP1_loss.png')
        plt.show()

if __name__ == '__main__':
    model = MLP(lr = 0.01,epoch=500,MLPSize=[2,5,1])
    model.fit()

结果: