深度学习方法中的其他学习方式

除了常规的预测，结果，深度学习中还有哪些不太常规的学习方式呢？

分两步优化法，两个不同时期的损失函数

深度学习与ACM的结合

CNN做图像分割的缺点：经多次下采样后，丢失高频信息，比如边缘、细小结构；传统的active contour模型的优点：曲线演化，擅长边缘定位；所以将CNN与active contour结合，是一种互补和促进。
https://zhuanlan.zhihu.com/p/163811140?utm_source=wechat_session

DARNet: Deep Active Ray Network for Building Segmentation

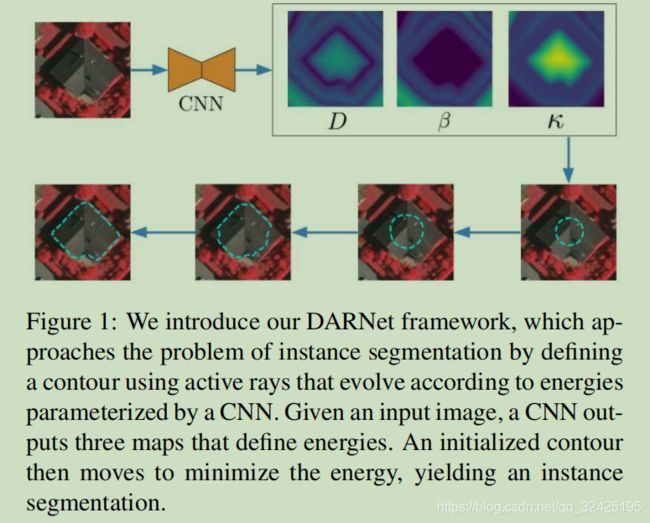
（1)Active Ray的轮廓表示:

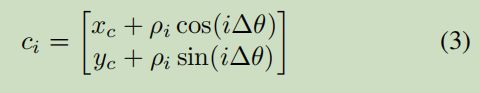
每一个边缘点都用ci表示
所有边缘点的能量项的公式记作：

它是所有边缘点能量的加和。每个边缘点的能量由3分布组成，分别代表我们希望预测的轮廓点是沿着边缘的；预测的轮廓的曲率要小，不要歪歪扭扭；轮廓是从很小的初始化开始，向外扩展的
每个点的3个能量项介绍
Data term:每个边缘点的ci的Data tern记作D(ci)，其中D是CNN输出的特征图，ci表示位置。
Data term:边缘处预测的值要尽量小->则D(ci)的值就会比较小->E(ci)的值比较小，从而起到最小化能量函数的目的

Curvature Term曲率项：

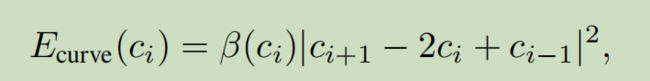
β(ci)是CNN输出的特征图β在ci位置的值，|ci+1 1 2ci + cii1|2是轮廓的二阶导数；
当预测输出的β比较大时，这个能量项让边缘拉直（二阶导数小），从而整体损失小

balloon term从小扩展项：

k是CNN输出的特征图； ρi是轮廓点的弧长，ρmax是当前轮廓的最大弧长；
该能量项希望轮廓更新时，从参考点逐步向外推进；
这样设置的目的是仅仅有Data term，不能够充分引导轮廓和边缘贴近，尤其是是参考点离边缘较远；曲率项的副作用是收缩轮廓，这里为了排除这个副作用
原理：ρi变大，ρi/ρmax就会变大，κ(ci)(1 1 ρi/ρmax)变小–>能量项变小

CNN输出D,B,K后，我们通过最小化能量函数来获得最优边界，即找到该建筑对应的所有的ci
通过能量项对ci求导–>ci是用极坐标表示的，ci=f(θi,ρi),θ是通过按一定角度分离选定的，所以就相当于只对ρi求导->对ρi求导，可以进一步转化为对欧几里得坐标系的x,y求导
pcos(i∆θ)=x,可以得出∂x/∂p=cos(i∆θ);同理，∂y/∂p=sin(i∆θ)

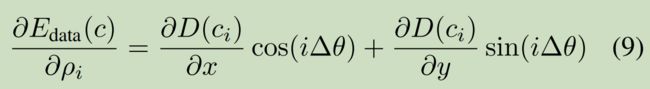
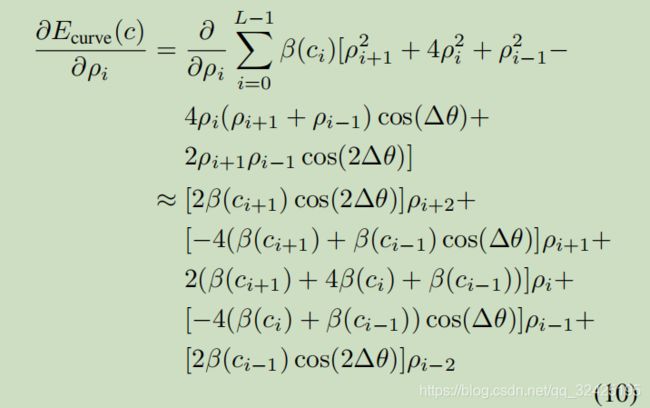
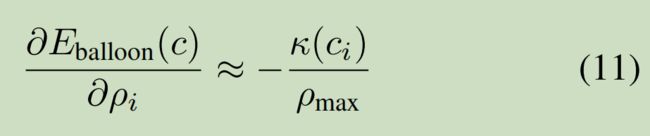
最后，得到整个能量项E对每个pi的偏导数:

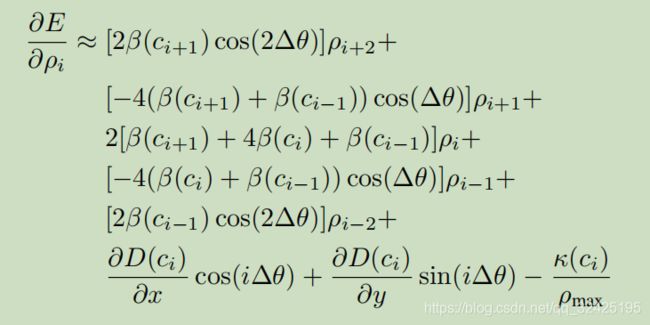
对所有pi的偏导数：

为了求解上述的方程，引入一个时间变量∆t，通过不断迭代让变量收敛，而得到最优解

当得到最优解后，就得到了预测的p_pre.使用相同的参考点和参考角度，可以得到p_gt,通过p_pre和p_gt间的L1_loss.

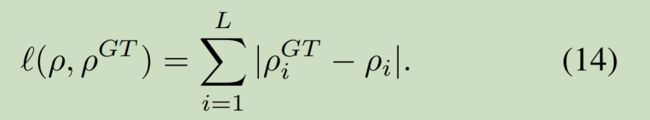
code
https://github.com/dcheng-utoronto/darnet

def run_vaihingen(split_num):
    train_baseline_vaihingen(split_num)
    pretrain_vaihingen(split_num)
    train_vaihingen(split_num)
    eval_baseline_vaihingen(split_num)
    eval_vaihingen(split_num)

def train_vaihingen(split_num=1):
    importlib.reload(dar_package.config)
    config = dar_package.config.config
    print("Train vaihingen {}".format(split_num))
    checkpoint_path = train_contours.run(config['vaihingen_exp_{}'.format(split_num)],
                                         config,
                                         vaihingen.VaihingenDataset,
                                         DRNContours,
                                         split_num)

model_and_loss = ModelAndLoss(Network, restore).to(device)
输入：sample[‘image’]
输出：beta, data, kappa
损失计算：

初始点的中心坐标和弧长是gt给定的，init_contour:给定弧长，默认为20，init_contour_origin给定中心坐标；
        loss, contour_x, contour_y, contour_rho = self.distance_loss(
                sample['init_contour'],
                sample['interp_radii'],
                sample['init_contour_origin'],
                beta,
                data,
                kappa,
                sample['interp_angles'],
                sample['delta_angles']
        )
几个字段解析：
init_contour:根据init_contour_radius=20, discretize_points=60,得到init_contour为一个列表，[20,20,20,......20]，共60项目
interp_radii：gt raddi,根据interp_angles和实际的轮廓计算得到实际的弧长列表，共60项，与discretize_points=60相对应
'init_contour_origin：应该是一个坐标，从gt_mask中随机选择的一个点
interp_angles：是一个列表，将360度平均且分为60份，[0,6,12,....360]共60项
delta_angles：角度间隔6


获得初始点中心坐标origin和初始点的范围后，开始计算实际的坐标点（注意：每个点的角度是给定的，初始中心点是给定的，只有弧长在不断变化）
contour_x = origin[:, 0].unsqueeze(1) + rho * cos_theta
 contour_y = origin[:, 1].unsqueeze(1) + rho * sin_theta
不断迭代来最优化求解，直到达到最大次数（max_steps=128），返回计算得到的每个角度对应的最佳弧长

然后，用L1 loss和gt轮廓计算的弧长做损失，优化网络。


根据初始点的坐标和范围，通过预测的beta, data, kappa，得到估计的轮廓：result
        result = evolve_active_rays_fast(
            rho_init, beta, data, kappa, 
            theta, delta_theta, rho_target, origin,
            delta_t=self.delta_t, max_steps=self.max_steps, debug_hist=debug_hist)

Eval的过程：也是需要
rho_diff, _, new_rho_x, new_rho_y, init_x, init_y, output = model_and_loss(sample)