【论文笔记 - NeRFs - ECCV2020】NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
0背景介绍
用神经辐射场来表征场景,用于新视角图像生成任务。
0.1 View Synthesis
该任务是通过给定从不同视角获取的同一场景的一张或多张图片,来合成其他视角下的图片。以下图为例,输入是不同视角的图片,来建模三维场景,然后就可以从任意视角来得到一张二维图像。

0.2 Representing Scenes
在本文中指的是三维场景表征,将三维场景存储到计算机中,就要建立空间位置和属性之间的关系。分显式和隐式两大类方法,
-
显式:空间位置和属性之间一一对应,用大量离散数据来表征场景,要保存所有的数据,需要很大的存储空间(几个GB),并且分辨率与数据量挂钩,极大地限制了在高分辨率场景中的应用。例如mesh、point cloud、voxel等技术。
-
隐式:空间位置和属性之间进行建模,用一个连续函数来表征场景,只需要保存这个函数,存储量通常只有几MB,但是可以做到非常高的分辨率。例如表示单位球面的形状,只需要知道 x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x2+y2+z2=1 。
虽然已经有一些隐式的工作了,但在表征复杂几何时,效果不如显式,而本文是将隐式表征提到了一个新的高度。
0.3 Neural Radiance Fields
神经辐射场NeRF,本文的核心。在计算机图形学中,场(Field)是一种用来表征三维场景的数据结构,由许多三维点构成,每个点都有一些属性,例如带有颜色属性的点构成的场可以用来描述材质和光照,带有透明度属性的点构成的场可以用来描述形状。NeRF 是一种利用神经网络(MLP)来对场进行建模,是一种隐式表征三维场景的技术。
可以用下面这张图,将上面介绍的信息串在一起。左侧是三维场景表征,包含形状和外观两部分。有了表征之后,就可以根据相应的渲染技术(表征不同,渲染技术不同)得到图像。 反过来,也可以从图像来得到三维场景表征,也就是反渲染的过程,NeRF的工作就集中在这里了。
1. Rendering and Inverse Rendering
首先要确定一种渲染技术及其配套的三维场景表征方式。在 NeRF 中采用了体渲染技术(Volume Rendering)来得到二维图像,它能够渲染的是用软不透明度场(Soft Opacity Field)和辐射场(Radiance Field)表征的三维场景。
1.1 Volume Rendering
像素表现出的颜色不止是源于三维物体表面,而是来源于沿着光线的积分。如下图两个红框位置,拿照相机拍玻璃杯,虽然表面都是蓝色的,但由于透过玻璃后的物体颜色不同,导致最终在图像上表现出不一样的像素值。那么在计算每个位置的像素值时,需要沿着光线方向叠加所经过物体的颜色。

体渲染就是对这一过程进行了建模,使用计算机来模拟光线在三维空间中的传播过程。它把物质抽象成粒子群,光线在穿过时,会与粒子发生一些相互作用,如吸收、放射等,从而影响粒子所在位置的不透明度(Opacity),最终导致粒子颜色(RGB Color)对于最终成像有不同的权重。
举例来说明为什么只要颜色和不透明度就可以描述一个场景,当光线穿过一团云时,光线的强度会呈现一个逐渐衰减的过程,这是因为不透明度会逐渐累计,导致通过的光会越来越少,每个位置的颜色对最终成像的作用也会逐渐减小。当没有光线透过时,好比一块木板挡在光线的路径上,也就看不到后面的东西了。

因此,对于体渲染的方法,需要知道空间中任意一个点的颜色和不透明度。如上所示,沿着一条光线r,会采样N个点,它们有不同的颜色和不透明度,最后的成像过程就是计算这条射线上的积分。
体渲染过程就是下面的公式,推导可以参考这里,
C ( r ) = ∫ t n t f T ( t ) σ ( r ( t ) ) c ( r ( t ) , d ) d t , where T ( t ) = exp ( − ∫ t n t σ ( r ( s ) ) d s ) C(\mathbf{r})=\int_{t_{n}}^{t_{f}} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_{n}}^{t} \sigma(\mathbf{r}(s)) d s\right) C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt, where T(t)=exp(−∫tntσ(r(s))ds)
其中, r ( t ) = o + t d r(t)=o+td r(t)=o+td 表示一条射线, o o o 为相机原点, t t t 为采样间隔, d d d 为方向。 σ \sigma σ 表示该粒子的不透明度, c c c 表示颜色,显然粒子的不透明度越高,颜色的表现能力越强,所以由 σ c \sigma c σc 表示该粒子受不透明度影响所呈现的颜色。 T T T 中计算了关于不透明度 σ \sigma σ 的积分的负指数幂,取值范围是0到1,表示光线从初始位置到当前位置之前没有碰到任何粒子的概率,例如没有碰到任何粒子,那么 T T T 就是1,也就是可以直接看到当前位置的粒子颜色 σ c \sigma c σc 。
在计算机中,需要对这个积分离散化计算,
C ^ ( r ) = ∑ i = 1 N T i ( 1 − exp ( − σ i δ i ) ) c i , where T i = exp ( − ∑ j = 1 i − 1 σ j δ j ) \hat{C}(\mathbf{r})=\sum_{i=1}^{N} T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \mathbf{c}_{i}, \text { where } T_{i}=\exp \left(-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}\right) C^(r)=∑i=1NTi(1−exp(−σiδi))ci, where Ti=exp(−∑j=1i−1σjδj)
其中, δ j = t i + 1 − t i \delta_j=t_{i+1}-t_{i} δj=ti+1−ti 是相邻采样点之间的距离。
1.2 Soft Opacity Field
每个空间位置 ( x , y , z ) (x,y,z) (x,y,z) 对应一个不透明度 σ \sigma σ。在渲染时,需要考虑光线在穿过粒子时的相互作用,通过不透明度就可以描述相互作用对光线带来的影响。

1.3 Radiance Field
外观包含了材质和光照两部分,NeRF中采用了辐射场将材质和光照打包在一起进行表征。思想是说空间中一个点 ( x , y , z ) (x,y,z) (x,y,z) ,从不同角度 ( θ , ϕ ) (\theta, \phi) (θ,ϕ) 观察,会表现出不同的颜色 r g b rgb rgb(由于采用了两个自由度来描述观察角度,并且做了归一化,所以每个点呈现的颜色变化就是一个圆)。材质和光照是耦合的,会相互影响,所以不利于编辑。
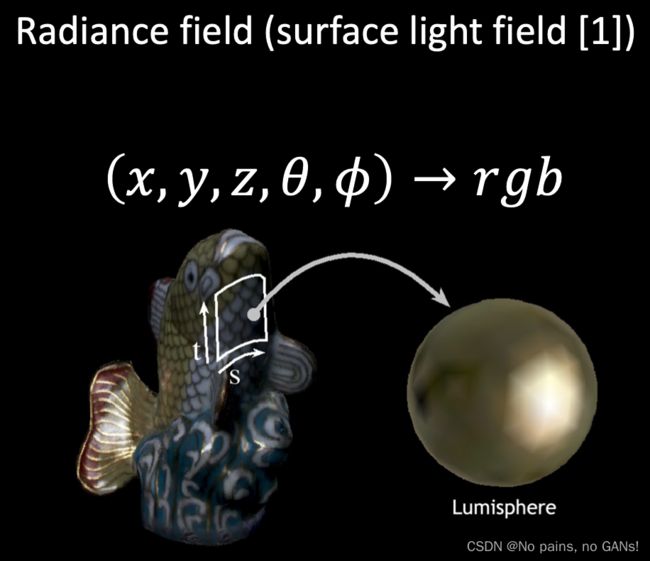
总结来说,NeRF 采用了颜色和不透明度来表征三维场景,配套使用体渲染技术根据三维场景生成二维图像。而对于反渲染过程,是根据空间位置和视角来得到颜色和不透明度,其中不透明度是关于空间位置的函数,而颜色不仅与空间位置有关,还与视角有关。
2 流程
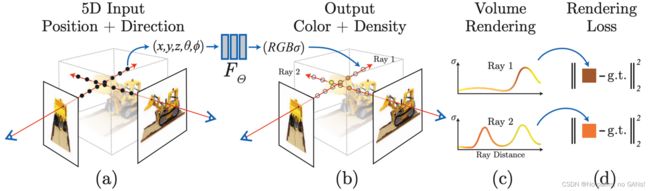
NeRF 采用隐式方法来表征场景,也就是通过一个函数 F Θ F_{\Theta} FΘ(MLP),将 ( x , y , z , θ , ϕ ) (x,y,z,\theta,\phi) (x,y,z,θ,ϕ) 映射为 ( r , g , b , σ ) (r,g,b,\sigma) (r,g,b,σ)。
-
(a) 在一条射线上采样 n 个点,它们具有相同的视角 ( θ , ϕ , 1 ) (\theta, \phi,1) (θ,ϕ,1) ;
-
(a)–>(b) 通过 MLP 将五维向量映射为不透明度和颜色;
-
(b)–>© 使用体渲染技术将射线上的值做积分得到渲染后的像素值;
因为体渲染是可微的,就可以用梯度下降来优化 MLP。这条射线对应的真实值,就是它与成像平面的交点位置的像素值,计算两者之间的误差,来监督训练过程。
3 Tricks
3.1 Positional Encoding
先前的工作发现,直接将低维向量输入到深层网络中,会倾向于学习低频的信息,也就导致了模糊,反之,如果使用高频函数将输入映射到更高维空间,可以更好地拟合包含高频变化的数据。因此,采用位置编码将输入的五维向量映射到更高维空间,如下所示,
γ ( p ) = ( sin ( 2 0 π p ) , cos ( 2 0 π p ) , ⋯ , sin ( 2 L − 1 π p ) , cos ( 2 L − 1 π p ) ) \gamma(p)=\left(\sin \left(2^{0} \pi p\right), \cos \left(2^{0} \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right) γ(p)=(sin(20πp),cos(20πp),⋯,sin(2L−1πp),cos(2L−1πp))
对于空间位置 ( x , y , z ) (x,y,z) (x,y,z), L = 10 L=10 L=10,还会再连接一个本身,因此每个值都扩展为 2 × 10 + 1 = 21 2\times10+1=21 2×10+1=21 维,那么位置就从三维转换为了 21 × 3 = 63 21\times3=63 21×3=63 维。对于视角额外增加的一位 ( θ , ϕ , 1 ) (\theta, \phi,1) (θ,ϕ,1), L = 4 L=4 L=4,其他类似,总共转化为 27 维。ref
Graf中提到,颜色随2d视角的变化要比3d坐标的变化平滑,所以视角的向量长度比较短。也就是说,某一个空间位置处的颜色随视角的变化比较小。
As the volume color c varies more smoothly with the viewing direction than with the 3D location, the viewing direction is typically encoded using fewer components, i.e., Ld < Lx.
(在transformer中也有用到位置编码,是给每个token分配一个位置信息,进而保证顺序。所以两者的编码意义不同)
3.2 Hierarchical Volume Sampling
分层采样方案来自于经典渲染技术,在前述的体渲染 (Volume Rendering) 方法中,对于射线上的点如何采样会影响最终的效率,如果采样点过多计算效率太低,采样点过少又不能很好地近似。那么就希望对于颜色贡献大的点附近采样密集,贡献小的点附近采样稀疏,基于这一想法,NeRF 提出了分层采样来提高效率,具体来说,NeRF 使用了两个网络进行优化:coarse 和 fine。
- 下左图,在一条光线上,均匀采样 N c N_c Nc 个点,使用 coarse 网络预测不透明度。
先前已经提到体渲染的公式,
C ^ ( r ) = ∑ i = 1 N T i ( 1 − exp ( − σ i δ i ) ) c i , where T i = exp ( − ∑ j = 1 i − 1 σ j δ j ) \hat{C}(\mathbf{r})=\sum_{i=1}^{N} T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) c_{i}, \text { where } T_{i}=\exp \left(-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}\right) C^(r)=∑i=1NTi(1−exp(−σiδi))ci, where Ti=exp(−∑j=1i−1σjδj)
可以转换为,
$\hat{C}(\mathbf{r})=\sum_{i=1}^{N} \omega_{i}c_{i}, \text { where } \omega_{i}=T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) $
对权重 ω i \omega_i ωi 就表示当前位置的粒子颜色对最终成像的贡献,做归一化后, ω ^ i = ω i ∑ j = 1 N c ω j \hat\omega_i=\frac{\omega_i}{ {\textstyle \sum_{j=1}^{N_c}\omega_j} } ω^i=∑j=1Ncωjωi表示概率密度函数,也就是下图中的红线,
- 下右图,根据估计出的概率密度函数,再采样 N f N_f Nf 个点,然后再把所有的采样点一起输入到 fine 网络进行预测。

4 数据预处理
从上面的内容中,可以知道 NeRF 中 MLP 的输入为五维向量,由一个三维坐标和二维视角组成,如果在往前一点,五维向量是由图片信息提供的,显然从图片到五维向量还有一个 gap,在数据预处理阶段进行填补。
为了得到五维向量,ref
- 首先,建立相机坐标系,相机位于原点 O O O 处,并根据相机的**焦距(1个参数)**确定成像平面(忽略了光心的影响);
- 其次,成像平面上就是该相机位置拍摄到的照片,在上面取一点 P P P,确定一条从相机原点出发的射线 $\vec{OP} ,也就是下图中的红线。 ,也就是下图中的红线。 ,也就是下图中的红线。P$ 点是在图像的有效范围内,否则就没有意义,即需要**图像的长宽(2个参数)**来限制取点范围。
- 然后,在射线上采样,采样点的方向就是$\vec{OP} $,坐标位置都可以表示出来了。采样范围是有限的,为相机离物体最近和最远的距离(2个参数)。
- 最后,相机的位置是会移动的,它的坐标系也就在变动,需要统一到同一个坐标系,也就是被表征的三维场景所在的世界坐标系,这个坐标变换就需要通过旋转平移矩阵(12个参数),也就是相机的位姿。

总的来说,从图像到五维向量还需要额外的17个参数,在 NeRF 中分了两种情况,
- 如果有真实的三维场景表征,那么就可以渲染得到任意视角下的图片,并且17个参数也是已知的,可以直接作为训练集。
- 如果有只有真实的图像,那么就需要用 SfM 技术,为每张图片标定17个参数,作为训练集。ref
基于此,可以进一步完善一下整个NeRF的流程。
- 准备好图像(用于提供real像素值)和17个参数;
- 根据相机位姿和相机焦距得到成像平面,并根据图像的长宽限制成像范围;
- 取成像平面中某一位置(对应的real像素值是已知的),与相机位置的连线构成一条射线,得到二维的视角参数(实际是3D的参数,但可以简化为2D),在最近和最远距离内采样 n 个点,得到三维的位置参数,构成n个五维向量;
- 根据相机位姿参数转化到世界坐标系,送入MLP中,预测每个点的rgb和sigma;
- 此时并不会直接对采样点进行监督,而是根据体渲染得到fake像素值,通过real和fake之间的误差来监督训练。