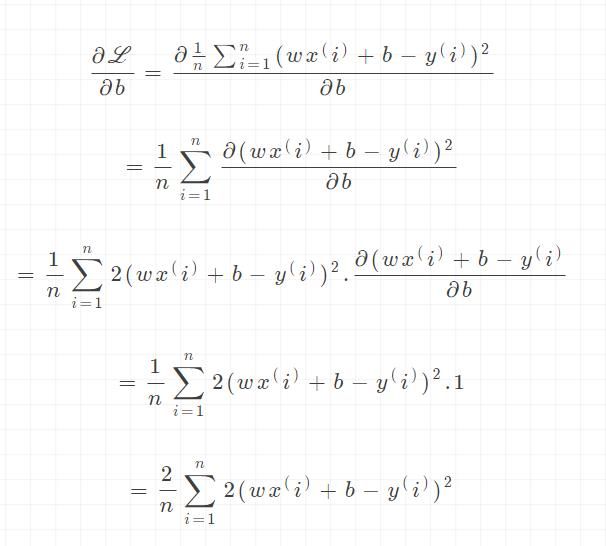多元回归求解 机器学习_机器学习之多元线性回归模型梯度下降公式与代码实现（篇二）...

欢迎转发与关注。

上一篇我们介绍了线性回归的概述和最小二乘的介绍,对简单的一元线性方程模型手推了公式和python代码的实现。

机器学习之线性回归模型详细手推公式与代码实现(篇一)

今天这一篇来介绍多元线性回归模型

多元线性回归模型介绍

在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。因此多元线性回归比一元线性回归的实用意义更大

比如糖尿病人的血糖变化可能受胰岛素、糖化血红蛋白、血清总胆固醇、甘油三酯等多种指标的影响。但很多情况下，由于自变量的单位是不一样的，需要做标准化处理。比如在消费水平预测模型中，工资水平、受教育程度、职业、地区、家庭负担等因素都会影响到消费水平，而这些影响因素的单位和量级肯定是不同的，虽然不会影响自变量的重要程度，但是对回归系数的大小还是有直接影响作用的。标准化回归系数没有单位，其值越大，说明该自变量对因变量的影响越大。

数学模型

1.描述因变量 y 如何依赖于自变量 X1，X2，…，Xn 和误差项ε的方程，称为多元回归模型

2.涉及n个自变量的多元回归模型可表示为

应变量Y可以近似地表示为自变量x1,x2,…,xm的线性函数ω0为常数项ω1,ω2,…,ωm是偏回归系数，表示在其他变量不变时时候x增加一个或者减少一个单位时候，Y的平均变化量ε是被称为误差项的随机变量，又称为残差3.参数 ∶= {1,2,3,…,,}确定了模型的状态，通过固定参数即可确定此模型的处理逻辑。当输入节点数 = 1时，数学模型可进一步简化为最简单的模型

= +

4.对于某个神经元来说，和的映射关系f。,是未知但确定的。两点即可确定一条直线，为了估计和的值，我们只需从图中直线上采样任意2个数据点就可以表示这条直线。

5.可以看到，只需要观测两个不同数据点，就可完美求解单输入线性模型的参数，对于n输入的现象模型，只需要采样n + 1组不同数据点即可，似乎线性模型可以得到完美解决。那么上述方法存在什么问题呢？考虑对于任何采样点，都有可能存在观测误差

= + +

6.一旦引入观测误差后，即使简单如线性模型，如果仅采样两个数据点，可能会带来较大估值偏差。如果基于蓝色矩形块的两个数据点进行估计，则计算出的蓝色虚线与真实橙色直线存在较大偏差。为了减少观测误差引入的估计偏差，可以通过采样多组数据样本集合 =

，然后找出一条“最好”的直线，使得它尽可能地让所有采样点到该直线的误差之和最小

7.由于观测误差的存在，当我们采集了多个数据点时，可能不存在一条直 线完美的穿过所有采样点。退而求其次，我们希望能找到一条比较“好”的位于采样点中 间的直线。那么怎么衡量“好”与“不好”呢？一个很自然的想法就是，求出当前模型的 所有采样点上的预测值() +与真实值()之间的差的平方和作为总误差

然后搜索一组参数,使得最小，对应的直线就是我们要寻找的最优直线

梯度下降法介绍

根据上面数学分析，我们确定用梯度下降法来计算多元线性模型，当然还有更多计算方式。

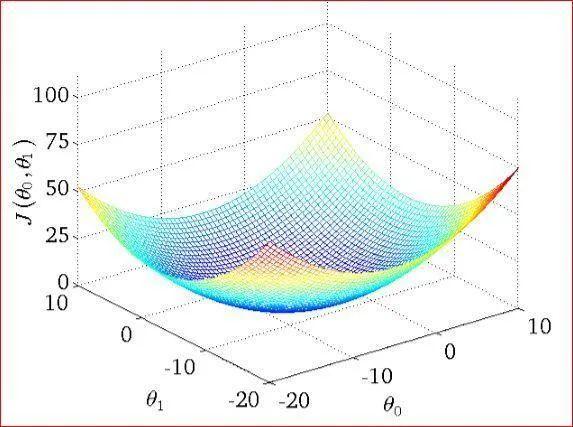
梯度下降法又称最速下降法，是求解无约束最优化问题的一种最常用的方法，在对损失函数最小化时经常使用。梯度下降法是一种迭代算法。选取适当的初值x(0)，不断迭代，更新x的值，进行目标函数的极小化，直到收敛。由于负梯度方向时使函数值下降最快的方向，在迭代的每一步，以负梯度方向更新x的值，从而达到减少函数值的目的

关于梯度下降算法的直观理解，我们以一个人下山为例。比如刚开始的初始位置是在红色的山顶位置，那么现在的问题是该如何达到蓝色的山底呢？按照梯度下降算法的思想，它将按如下操作达到最低点：

第一步，明确自己现在所处的位置第二步，找到相对于该位置而言下降最快的方向第三步， 沿着第二步找到的方向走一小步，到达一个新的位置，此时的位置肯定比原来低第四部， 回到第一步第五步，终止于最低点按照以上五步，最终达到最低点，这就是梯度下降的完整流程。当上图并不是标准的凸函数，往往不能找到最小值，只能找到局部极小值。所以你可以用不同的初始位置进行梯度下降，来寻找更小的极小值点，当然如果损失函数是凸函数就没必要了

计算梯度

根据之前介绍的梯度下降算法，我们需要计算出函数在每一个点上的梯度信息

/

/b

需要优化的模型参数是和，因此我们按照下面方式循环更新参数，其中为学习率

学习率(步长)介绍

我们可以通过来控制每一步走的距离，以保证不要走的太快，错过了最低点(右图所示)，同时也要保证收敛速度不要太慢

所以在选择大小的时候在梯度下降中是非常重要的，不能太大也不能太小

代码实现

引入依赖import numpy as npimport matplotlib.pyplot as plt

导入数据points = np.genfromtxt('linear.csv', delimiter=',')points[0,0]# 提取points中的两列数据，分别作为x，yx = points[:, 0]y = points[:, 1]# 用plt画出散点图plt.scatter(x, y)plt.show()效果

定义损失函数# 损失函数是系数的函数，另外还要传入数据的x，ydefcompute_cost(w, b, points): total_cost = 0 M = len(points)# 逐点计算平方损失误差，然后求平均数for i in range(M): x = points[i, 0] y = points[i, 1] total_cost += ( y - w * x - b ) ** 2return total_cost/M

定义模型的超参数alpha：学习率num_iter：训练优化 10次(可以自行设定)alpha = 0.0001initial_w = 0initial_b = 0num_iter = 10

定义核心梯度下降算法函数defgrad_desc(points, initial_w, initial_b, alpha, num_iter): w = initial_w b = initial_b# 定义一个list保存所有的损失函数值，用来显示下降的过程 cost_list = []for i in range(num_iter): cost_list.append( compute_cost(w, b, points) ) w, b = step_grad_desc( w, b, alpha, points )return [w, b, cost_list]defstep_grad_desc( current_w, current_b, alpha, points ): sum_grad_w = 0 sum_grad_b = 0 M = len(points)# 对每个点，代入公式求和for i in range(M): x = points[i, 0] y = points[i, 1] sum_grad_w += ( current_w * x + current_b - y ) * x sum_grad_b += current_w * x + current_b - y# 用公式求当前梯度 grad_w = 2/M * sum_grad_w grad_b = 2/M * sum_grad_b# 梯度下降，更新当前的w和b updated_w = current_w - alpha * grad_w updated_b = current_b - alpha * grad_breturn updated_w, updated_b

测试：运行梯度下降算法计算最优的w和bw, b, cost_list = grad_desc( points, initial_w, initial_b, alpha, num_iter )print("w is: ", w)print("b is: ", b)cost = compute_cost(w, b, points)print("cost is: ", cost)plt.plot(cost_list)plt.show()效果

w is: xxxxxxxxb is: xxxxxxxxcost is: xxxxxxxx

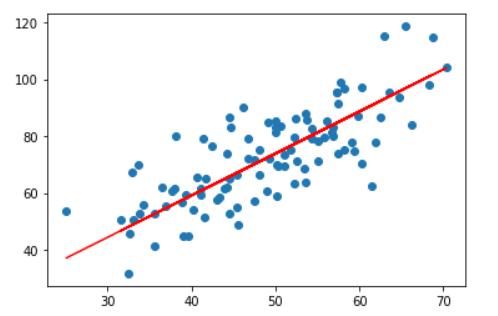
画出拟合曲线plt.scatter(x, y)# 针对每一个x，计算出预测的y值pred_y = w * x + bplt.plot(x, pred_y, c='r')plt.show()效果

上述例子比较好地展示了梯度下降算法在求解模型参数上的强大之处。需要注意的 是对于复杂的非线性模型，通过梯度下降算法求解到的和可能是局部极小值而非全局 最小值解，这是由模型函数的非凸性决定的。但是我们在实践中发现，通过梯度下降算法 求得的数值解，它的性能往往都能优化得很好，可以直接使用求解到的数值解和来近似作为最优解。

思考

首先假设个输入的数学模型为线性模型之后，只采样 + 1个数据点就可以估计线性模型的参数和。引入观测误差后，通过梯度下降算法，我们可以采样多组数据点循环优化得到和的数值解。如果我们换一个角度来看待这个问题，它其实可以理解为一组连续值(向量)的预测问题。给定数据集，我们需要从中学习到数据的真实模型，从而预测未见过的样本的输出值。在假定模型的类型后，学习过程就变成了搜索模型参数的问题，比如我们假设为线性模型，那么训练过程即为搜索线性模型的和参数的过程。训练完成后，利用学到的模型，对于任意的新输入，我们就可以使用学习模型输出值作为真实值的近似。从这个角度来看，它就是一个连续值的预测问题。

未完待续 ……欢迎关注