【深度学习笔记（五）】之卷积神经网络组成介绍

本文章由公号【开发小鸽】发布！欢迎关注！！！

老规矩–妹妹镇楼：

一. 卷积神经网络（CNN）

（一）结构组成

        经典的神经网络我们之间已经讲过了，现在我们要讲的是卷积神经网络。

        神经网络的结构是：

                输入层 + 隐藏层 + 激活函数 + 输出层

        卷积神经网络的组成：

                输入层 + 卷积层 + 激活函数 + 池化层 + 全连接层
                INPUT + CONV + RELU + POOL + FC

（二）卷积层：

        所谓的卷积类似于图像空间域处理的卷积操作，设置一个小区域的滤波器，将输入的图像按照滤波器的大小来分区域，然后将滤波器在输入图像的每一个区域上滑动，对于每一个区域都产生一个特征值。

        当滤波器把输入图像的所有区域求取了特征值后，就生成了一个特征图。该特征图中存储的就是滤波器在输入图像上产生的每一个特征值。

        可以看到，卷积时边缘信息利用是较少的。为了将这些边缘信息利用起来，在原始输入图像中加上一圈边缘0，记作(+pad 1)，添加了n层0，记为+pad n。原始图像的边缘现在就不是边缘了，同时，现在的边缘全为0，这些0对于特征值的提取没有意义，因此就算添加了一圈0也没有影响，它们的存在只是为了让原来的图像边缘有更多被计算的机会。

（三）卷积输出特征图尺寸

        该特征图的大小尺寸，是由输入图像的尺寸大小Input，滤波器的尺寸大小Filter，卷积的步长stride以及填充0的宽度pad来决定的。

        Output =( Input + 2 * Pad ) / stride + 1

        Output即为卷积输出的结果尺寸，深度为滤波器的个数。

        如输入图像的尺寸大小为 32 x 32 x 3，滤波器的尺寸大小为5 x 5 x 3。那么特征图的大小是由存储的特征值的多少决定的。

        对于输入图像的尺寸为 32 x 32，填充0的宽度为0，即没有填充，当步长为1时，滤波器 5 x 5在输入图像的每一行只能进行（32 +2 * 0– 5）/1 +1= 28次求取特征值。同理，每一列也是一样的，特征图中特征值的尺寸为 28 x 28个。

        当步长为2时，特征图的尺寸为(32 + 2 * 0 - 5)/2 +1 = 14，其中的除法是要向下取整的，即尺寸为14 x 14。

        当步长选取过大时，得到的特征值很少，但是计算量很小。
        当步长选取很小时，得到的特征值很多，但是计算量很大。

        我们也经常看到输入图像经过滤波器后有好几个特征图，这是因为用了多个滤波器来特征值。有几个滤波器，就有几个特征图。将得到的特征图都堆叠到一起，就得到了卷积层的输出结果。如下图所示，生成了两个特征图。

        卷积不仅可以在输入图像上进行，还可以在卷积后的输出特征图上进行。

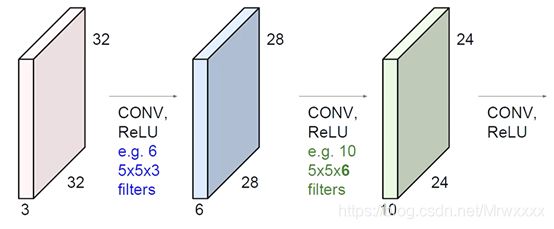
        如下图所示，第一次卷积操作后，通过6个滤波器，得到了6个特征图组成的卷积结果，再次对特征图进行卷积，通过10个滤波器，得到了10个特征图组成的卷积结果。

（四）池化层

        对特征图进行操作，将特征图压缩，也是用与卷积差不多的操作，选取小区域在特征图中滑动，在小区域中求取mean值或者Max值，用来代表这一小区域的特征值，即将这一小区域的特征值压缩为一个值。

（五）全连接层

        卷积神经网络最后的全连接层与经典神经网络的全连接层是一样的，它将前面卷积层，池化层后的特征图提取出来，计算该输入图像属于某个类别的概率。

二．卷积神经网络的优势

        经典的神经网络是全连接的网络，每个层次之间都是全连接的，参数非常庞大。

        但是卷积神经网络就将每个特征图的参数实现了共享，即每个特征图中的神经元对应的参数都是一样的。

        比如，卷积输出了2个特征图，输入图像的尺寸为 32 x 32 x 3， +pad2，Stride= 1，两个滤波器5 x 5 x 3，则输出的特征图尺寸为32 x 32 x 2，可以得知特征图中的特征值有 32 x 32个，而每一个特征值都是由滤波器对输入图像卷积得来的，即每个特征值对应输入图像中的一个5 x 5 x 3区域，即75个参数，而每个特征值的参数都是不同的，因此如果是全连接的话，共有32 x 32 x 5 x 5 x 3个参数，这个数字太庞大了，对计算效率不利。

        卷积神经网络将每个特征值对应的75个参数都共享了，即每个特征图中32 x 32个特征值的参数都是一样的。那么如果是两个特征图就只需要 75 x 2 = 150个参数。