matlab数学建模-非线性规划（无约束规划、有约束规划）

目录

二次规划，沃尔夫法

无约束规划

有约束规划

---

非线性规划的标准形式：

gi(x), hj(x)是约束条件，gi(x), hj(x)和f(x)中至少有一个是非线性函数。

非线性模型按照约束条件分：

1）无约束非线性规划模型

2）等式约束非线性规划模型

3）不等式约束非线性规划模型

---

二次规划，沃尔夫法

案例: 

H和A是矩阵，f和b是列向量

代码如下

clear all
clc
H=[1 -1;-1 2];
f=[-2;-6];
A=[1 1;-1 2;2 1];
b=[2 2 3];
lb=zeros(2,1);
[x,fval,exitflag]=quadprog(H,f,A,b,[],[],lb)

无约束规划

三个功能函数  fminbnd、fminsearch、fminunc 

fminbnd:

求固定区间，单变量函数最小值（一元函数最小值问题）

clear all
clc
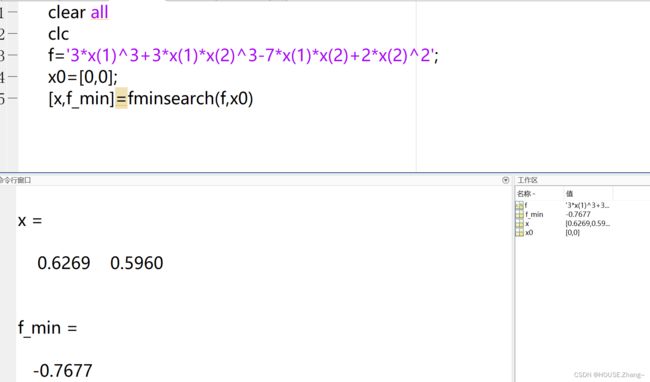
[x,y_min]=fminbnd('sin(2*x)',0,2*pi)

 fminsearch：

clear all
clc
f='3*x(1)^3+3*x(1)*x(2)^3-7*x(1)*x(2)+2*x(2)^2';
x0=[0,0];
[x,f_min]=fminsearch(f,x0)

fminunc ：

函数

 脚本调用

 那段英文我搜了一下，Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.（优化完成，因为梯度的大小小于最优容差的值。）

 x,fval值工作区直接看，也可以命令行输入x,fval查看

---

有约束规划

fmincon函数，求多变量，有约束，非线性函数的最小值

案例1

 

代码：

目标函数

function f=ex10_6a(x)
f=x(1)*x(1)*(x(2)+2)*x(3);

条件函数

function [c,ceq]=ex10_6b(x)
c(1)=350-163*x(1)^(-2.86)*x(3)^(0.86);
c(2)=10-4*10^(-3)*x(1)^(-4)*x(2)*x(3)^3;
c(3)=x(1)*(x(2)+1.5)+0.0044*x(1)^(-4)*x(2)*x(3)^3-3.7*x(3);
c(4)=375-3.56*10^5*x(1)*x(2)^(-1)*x(3)^(-2);
c(5)=4-x(3)/x(1);
ceq=0;

函数求解程序

clear all
clc
x0=[2 25 20]';
lb=[1 4.5 10]';
ub=[4 50 30]';
[x,fval,exitflag]=fmincon(@ex10_6a,x0,[],[],[],[],lb,ub,@ex10_6b)

结果

 案例2

 

代码

clear all
clc
%初值x0
x0=[10;10;10];
A=[-1 -2 -2;1 2 2];
b=[0;72];
[x,fval]=fmincon('-x(1)*x(2)*x(3)',x0,A,b);