二阶魔方还原 C++ BFS

建立搜索算法完成从任意初始状态向目标状态的操作转换

二阶魔方示意图如下：

问题定义

将二阶魔方展开如下图

其中$l_1,l_2,...,l_{12}$均为二维矩阵，代表所在行的两个方块颜色。
我们使用1至6代表六种不同的颜色，则还原后的展开图表达式为：

$[[l_1,l_2],[l_3,l_4],...,[l_{11},l_{12}]]=[[11,11],[22,22],...,[66,66]]$

操作定义

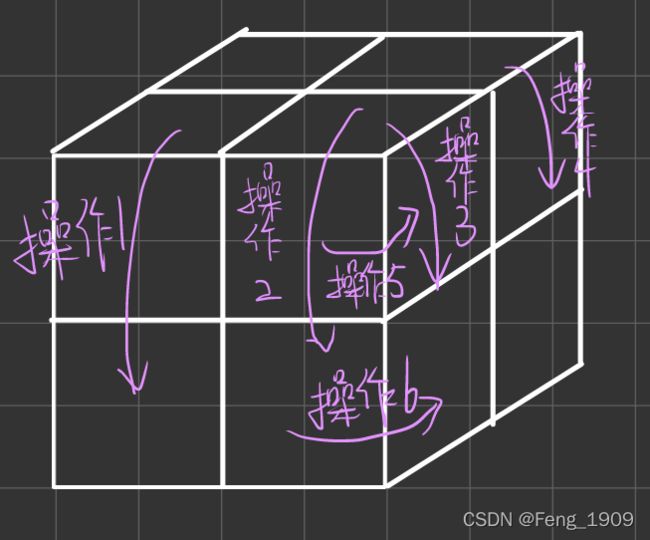
我们定义6种操作方法，可以完成魔方的任意自由度地旋转，具有空间完备性，其实3种操作足以还原魔方，但是可能结果不是最优解，也可以定义12种操作方式，但是这12种操作方式包含了6种冗余操作，除了增加编程难度以外没有任何好处

下面展示这六种操作：

算法实现

涉及算法：

BFS

广度优先搜索，又称宽搜，信竞基础，不多介绍

递归

函数自己调用自己，信竞基础，不多介绍

好了，可以愉快敲代码了

代码很简单，但是贼难敲，且费脑细胞

/*
***********************
**  Author:Feng1909  **
***********************
*/ 

#include 
#include 
#include 
#include 

using namespace std;

// 定义一个结构体，存储魔方每一个状态以及在对应状态时刻之前的操作
struct magic_cube{
    int a[13][3];
    queue<int> steps;
}init;

// 用于BFS算法，普通BFS算法使用队列实现
queue<magic_cube> q;

// 是否复原
bool flag = 0;

// 读取输入
void input_cube() {
	cout<<"input cube: "<<endl;
    for (int i=1; i<=12; i++) {
        for (int j=1; j<=2; j++)
            cin>>init.a[i][j];
    }
}

// 暴力检测是否复原
bool is_back(magic_cube t) {
    if (t.a[1][1] == t.a[1][2] && t.a[1][1] == t.a[2][1] && t.a[1][1] == t.a[2][2] &&
        t.a[3][1] == t.a[3][2] && t.a[3][1] == t.a[4][1] && t.a[3][1] == t.a[4][2] &&
        t.a[5][1] == t.a[5][2] && t.a[5][1] == t.a[6][1] && t.a[5][1] == t.a[6][2] &&
        t.a[7][1] == t.a[7][2] && t.a[7][1] == t.a[8][1] && t.a[7][1] == t.a[8][2] &&
        t.a[9][1] == t.a[9][2] && t.a[9][1] == t.a[10][1] && t.a[9][1] == t.a[10][2] &&
        t.a[11][1] == t.a[11][2] && t.a[11][1] == t.a[12][1] && t.a[11][1] == t.a[12][2])
         return true;
    else return false;
}

// 对应操作1
// 特别烧脑，脑细胞毁灭者
void act_1(magic_cube t) {
    magic_cube tmp;
    tmp = t;
    tmp.a[5][1] = t.a[1][1];
    tmp.a[6][1] = t.a[2][1];
    tmp.a[1][1] = t.a[10][2];
    tmp.a[2][1] = t.a[9][2];
    tmp.a[11][1] = t.a[5][1];
    tmp.a[12][1] = t.a[6][1];
    tmp.a[10][2] = t.a[11][1];
    tmp.a[9][2] = t.a[12][1];
    tmp.a[3][1] = t.a[4][1];
    tmp.a[3][2] = t.a[3][1];
    tmp.a[4][1] = t.a[4][2];
    tmp.a[4][2] = t.a[3][2];
    tmp.steps.push(1);
    if(is_back(tmp)) {
    	flag = 1;
        cout<<tmp.steps.size()<<endl;
		cout<<"steps: "<<endl;
        while (!tmp.steps.empty()){
        	cout<<tmp.steps.front()<<endl;
        	tmp.steps.pop();
		}
	}
    q.push(tmp);
}

// 对应操作2
void act_2(magic_cube t) {
    magic_cube tmp;
    tmp = t;
    tmp.a[5][2] = t.a[1][2];
    tmp.a[6][2] = t.a[2][2];
    tmp.a[1][2] = t.a[10][1];
    tmp.a[2][2] = t.a[9][1];
    tmp.a[11][2] = t.a[5][2];
    tmp.a[12][2] = t.a[6][2];
    tmp.a[10][1] = t.a[11][2];
    tmp.a[9][1] = t.a[12][2];

    tmp.a[7][1] = t.a[7][2];
    tmp.a[7][2] = t.a[8][2];
    tmp.a[8][1] = t.a[7][1];
    tmp.a[8][2] = t.a[8][1];
    
    tmp.steps.push(2);
    if(is_back(tmp)) {
    	flag = 1;
        cout<<tmp.steps.size()<<endl;
		cout<<"steps: "<<endl;
        while (!tmp.steps.empty()){
        	cout<<tmp.steps.front()<<endl;
        	tmp.steps.pop();
		}
	}
    q.push(tmp);
}

// 对应操作3
void act_3(magic_cube t) {
    magic_cube tmp;
    tmp = t;
    tmp.a[2][1] = t.a[4][2];
    tmp.a[2][2] = t.a[3][2];
    tmp.a[3][2] = t.a[11][1];
    tmp.a[4][2] = t.a[11][2];
    tmp.a[11][1] = t.a[8][1];
    tmp.a[11][2] = t.a[7][1];
    tmp.a[8][1] = t.a[2][2];
    tmp.a[7][1] = t.a[2][1];

    tmp.a[5][2] = tmp.a[5][1];
    tmp.a[5][1] = tmp.a[6][1];
    tmp.a[6][1] = tmp.a[6][2];
    tmp.a[6][2] = tmp.a[5][2];

    tmp.steps.push(3);
    if(is_back(tmp)) {
    	flag = 1;
        cout<<tmp.steps.size()<<endl;
		cout<<"steps: "<<endl;
        while (!tmp.steps.empty()){
        	cout<<tmp.steps.front()<<endl;
        	tmp.steps.pop();
		}
	}
    q.push(tmp);
}

// 对应操作4
void act_4(magic_cube t) {
    magic_cube tmp;
    tmp = t;
    tmp.a[1][1] = t.a[4][1];
    tmp.a[1][2] = t.a[3][1];
    tmp.a[3][1] = t.a[12][1];
    tmp.a[4][1] = t.a[12][2];
    tmp.a[12][1] = t.a[8][2];
    tmp.a[12][2] = t.a[7][2];
    tmp.a[8][2] = t.a[1][2];
    tmp.a[7][2] = t.a[1][1];

    tmp.a[9][1] = tmp.a[9][2];
    tmp.a[9][2] = tmp.a[10][2];
    tmp.a[10][2] = tmp.a[10][1];
    tmp.a[10][1] = tmp.a[9][1];

    tmp.steps.push(4);
    if(is_back(tmp)) {
    	flag = 1;
        cout<<tmp.steps.size()<<endl;
		cout<<"steps: "<<endl;
        while (!tmp.steps.empty()){
        	cout<<tmp.steps.front()<<endl;
        	tmp.steps.pop();
		}
	}
    q.push(tmp);
}

// 对应操作5
void act_5(magic_cube t) {
    magic_cube tmp;
    tmp = t;
    tmp.a[5][2] = t.a[3][2];
    tmp.a[5][1] = t.a[3][1];
    tmp.a[3][1] = t.a[9][1];
    tmp.a[3][2] = t.a[9][2];
    tmp.a[9][1] = t.a[7][1];
    tmp.a[9][2] = t.a[7][2];
    tmp.a[7][1] = t.a[5][1];
    tmp.a[7][2] = t.a[5][2];

    tmp.a[1][1] = t.a[1][2];
    tmp.a[1][2] = t.a[2][2];
    tmp.a[2][2] = t.a[2][1];
    tmp.a[2][1] = t.a[1][1];

    tmp.steps.push(5);
    if(is_back(tmp)) {
    	flag = 1;
        cout<<tmp.steps.size()<<endl;
		cout<<"steps: "<<endl;
        while (!tmp.steps.empty()){
        	cout<<tmp.steps.front()<<endl;
        	tmp.steps.pop();
		}
	}
    q.push(tmp);
}

// 对应操作6
void act_6(magic_cube t) {
    magic_cube tmp;
    tmp = t;
    tmp.a[6][2] = t.a[4][2];
    tmp.a[6][1] = t.a[4][1];
    tmp.a[4][1] = t.a[10][1];
    tmp.a[4][2] = t.a[10][2];
    tmp.a[10][1] = t.a[8][1];
    tmp.a[10][2] = t.a[8][2];
    tmp.a[8][1] = t.a[6][1];
    tmp.a[8][2] = t.a[6][2];

    tmp.a[11][1] = t.a[12][1];
    tmp.a[11][2] = t.a[11][1];
    tmp.a[12][2] = t.a[11][2];
    tmp.a[12][1] = t.a[12][2];

    tmp.steps.push(6);
    if(is_back(tmp)) {
    	flag = 1;
        cout<<tmp.steps.size()<<endl;
		cout<<"steps: "<<endl;
        while (!tmp.steps.empty()){
        	cout<<tmp.steps.front()<<endl;
        	tmp.steps.pop();
		}
	}
    q.push(tmp);
}

// 遍历每一种操作
void search(magic_cube t, int num) {
    switch(num) {
        case 1: act_1(t); break;
        case 2: act_2(t); break;
        case 3: act_3(t); break;
        case 4: act_4(t); break;
        case 5: act_5(t); break;
        case 6: act_6(t); break;
        default: break;
    }
}

// 核心递归算法
void find_best() {
	if(flag) return; // 如果找到，就退出递归
    search(q.front(), 1);
    search(q.front(), 2);
    search(q.front(), 3);
    search(q.front(), 4);
    search(q.front(), 5);
    search(q.front(), 6);
    q.pop();
    find_best();
}

// 主函数入口
int main() {
    input_cube();
    q.push(init);
    find_best();
}

测试样例：

5 1 5 1 2 2 2 2 1 3 1 3 4 4 4 4 5 6 5 6 3 6 3 6

显然，只需要拧一下就可以复原
输出：

input cube:
1
steps:
2

第一行代表总的操作次数，第二行代表从第一次操作开始的所有操作编号