论文翻译:STGAT: Modeling Spatial-Temporal Interactions for Human Trajectory
STGAT: Modeling Spatial-Temporal Interactions for Human Trajectory
- 摘要
- 1 引言
- 2 相关工作
- 3 Method
- 4 实验
- 5 结论
STGAT:为人类轨迹建模时空交互作用
收录于ICCV 2019
作者:Huang Y, Bi H K, Li Z, et al.
论文地址:ICCV 2019
发表时间:ICCV2019
备注:
论文解析
开源 √ :https://github.com/huang-xx/STGAT
代码解析√ :https://blog.csdn.net/u010730851/article/details/106580342
摘要
大多数现有方法都忽略了与场景中其他行人交互的时间相关性。
在这项工作中,我们提出了一种时空图注意力网络(STGAT),该网络基于序列到序列的体系结构来预测行人的未来轨迹。
除了图注意力机制在每个时间步长捕获的空间交互作用之外,
我们还采用了额外的LSTM来编码交互作用的时间相关性。
人群数据集(ETH和UCY)上实现了卓越的性能
1 引言
与局部邻域假设的限制不同,“注意”机制有助于对行人之间的相对影响和潜在的空间相互作用进行编码,因为相邻行人对轨迹预测的重要性不同。
与“合并”方案相比,通过为行人分配不同的适应性重要性,基于注意力的模型可以基于空间交互作用更好地了解人群的行为。
然而,尽管已经对各个方面进行了充分的研究,但在先前的工作中却忽略了一个因素。
除了在同一时间步长进行空间交互之外,人群中交互的时间连续性也是必需的。
如图1所示,在现有的轨迹预测工作中,已经很好地考虑了行人B和C在时间点的空间相互作用的影响。
但是,由于人类运动的连续性和前瞻性,行人需要考虑其他人的历史运动来确定他们当前的运动行为,以避免将来发生潜在的碰撞。
例如,当行人A计划轨迹时,应考虑行人B和C从t−∆t到t的相互作用。因此,人群中相互作用的时间相关性起着重要的作用。
为了解决上述局限性,我们构建了一个新颖的时空图注意力网络(称为STGA T),在该网络中分别对行人之间的时空交互进行了编码。
1.图注意力(GAT)方案[32]捕获了一个时间步的空间相互作用,该方案对场景中涉及的所有行人建模。
2.为行人分配了不同的重要性后,使用一个额外的LSTM来捕获交互的时间相关性。
3.汇总所有行人之间的所有时空相互作用,未来的轨迹将由我们的序列到序列(seq2seq)体系结构生成。为
4.了模拟多式联运,我们采用品种损失[12]来产生多个社会上合理的输出。
贡献:
我们提出了一个新颖的框架(称为STGAT)来预测人类的轨迹。
1.首先,我们通过采用额外的LSTM显式建模交互作用的时间相关性。
2.其次,我们通过使用GAT汇总LSTM的隐藏状态来模拟行人之间的空间相互作用。
本文是在对行人运动进行建模的背景下,将GAT(图形注意力网络)与LSTM结合起来的首次尝试。
实验结果表明,图注意力网络可以合理地重视邻居,并且我们的模型可以预测不同场景下的合理轨迹。
2 相关工作
2.1 Crowd Interaction(人群互动)
2.2 Recurrent Neural Networks for Sequence Prediction(递归神经网络的序列预测)
2.3 Sequence to Sequence Model(序列到序列模型)
2.4 Graph Neural Network(图神经网络)
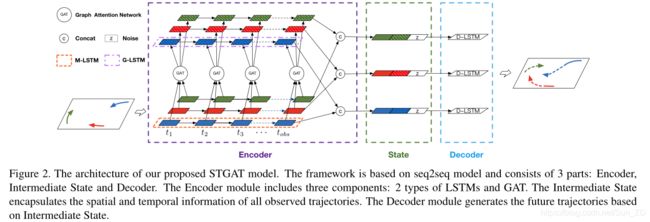
3 Method
编码器中包含三个组件:
1.基于LSTM的行人轨迹编码模块,
2.用于对空间交互进行建模的基于GAT的模块
3.用于捕获交互的时间相关性的基于LSTM的模块。
3.1. Problem Definition
场景中N个行人: p 1 , p 2 , . . . . . , p N p1,p2,.....,pN p1,p2,.....,pN,行人pi(i∈[1,N])在时间步t的位置:
S i t = ( x i t , y i t ) S_{i}^{t}=\left(x_{i}^{t}, y_{i}^{t}\right) Sit=(xit,yit)
已知:行人 i = 1 , 2 , . . . , N , i= 1,2,...,N, i=1,2,...,N,在时间步 t = 1 , 2 , . . . . , T o b s t=1,2,....,Tobs t=1,2,....,Tobs 的位置Sit
求 :行人 i = 1 , 2 , . . . , N , i= 1,2,...,N, i=1,2,...,N,在时间步 t = T o b s + 1 , . . . . , T p r e d t=Tobs+1,....,Tpred t=Tobs+1,....,Tpred 的位置Sit
3.2. Trajectory Encoding for One Pedestrian(一个行人的轨迹编码)
以下为提取单个行人在观察时间步内的信息
1.首先计算每个行人与上一个时间步的相对位置

2.在每个时间步长中,并将这些向量即M-LSTM单元的输入

φ ( ⋅ ) φ(·) φ(⋅):嵌入函数
W e e W_ee Wee:嵌入权重
m i t m^t_i mit:是时间步t处MLSTM的隐藏状态
W m W_m Wm:M-LSTM单元的权重
这些参数在场景中的所有行人之间共享
3.3. 基于GAT的人群交互建模(基于GAT的人群交互建模)
以下为处理每个时刻(即每帧),共T个时间步(帧)的信息。
GAT对图结构化数据进行操作,并遵循自我关注策略,通过参与每个图节点的邻居来计算每个图节点的特征。 GAT是通过堆叠图注意层来构造的。我们在图4中说明了一个图关注层。
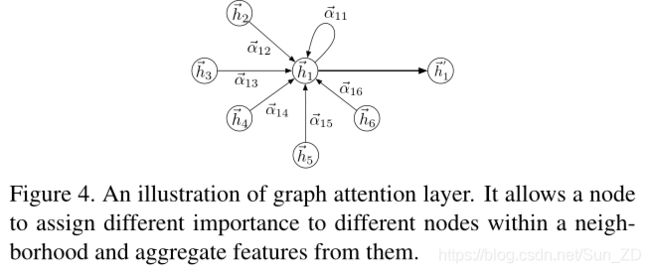
图4 图形注意层,允许节点为邻域内的不同节点分配不同的重要性,并从中聚合特征。
图关注层的输入: h = h 1 , h 2 , . . . , h N , h i ∈ R F h = {h_1,h_2, ..., h_N} , h_i \in R^F h=h1,h2,...,hN,hi∈RF
N:节点数
F:每个节点的特征维数
图关注层的输出: h ′ = { h ⃗ 1 ′ , h ⃗ 2 ′ , … , h ⃗ N ′ } h^{\prime}=\left\{\vec{h}_{1}^{\prime}, \vec{h}_{2}^{\prime}, \ldots, \vec{h}_{N}^{\prime}\right\} h′={h1′,h2′,…,hN′}
节点输入输出的特征维数可以不相等。
…
在观察时间步中
图形关注层输入: m i t ( t = 1 , … , T o b s ) m_{i}^{t}\left(t=1, \ldots, T_{o b s}\right) mit(t=1,…,Tobs)
节点对(i,j)的注意力机制中的系数(图4的边)可以通过以下公式计算:
∣ ∣ || ∣∣:串联运算
⋅ T ·T ⋅T:表示换位
α i j t α^t_{ij} αijt:是时间步t处节点j对i的关注系数
N i Ni Ni:图上节点i的邻居
W ∈ R F ′ ∗ F W \in R^{F' * F} W∈RF′∗F:应用于每个节点的共享线性变换的权重矩阵
(F为mti的维数,F’为输出的维数)
a ∈ R 2 F ′ a \in R^{2F'} a∈R2F′:单层前馈的权向量神经网络。
LeakyReLU的softmax函数标准化。
得到归一化的注意力系数后.
节点i在t时刻的一个图注意层输出为:
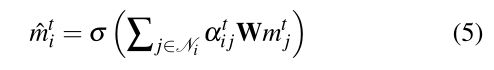
σ σ σ:非线性函数
等式4和等式5显示了单个图形注意层的工作方式。
在我们的实现中,采用了两个图形注意层。
m ^ i t \hat{m}_{i}^{t} m^it:(两个图关注层之后的结果)是行人i在t处的聚集隐藏状态,其中包含来自其他行人的空间影响。
3.4. Fusion of Spatial and Temporal Information(时空信息融合)
使用另一个LSTM显式地建模交互之间的时间相关性。我们将此LSTM称为G-LSTM:
![]()
m ^ i t \hat{m}_{i}^{t} m^it:来自公式5
W g W_g Wg:G-LSTM权重,在所有序列之间共享
编码器组件中,两个LSTM
M-LSTM:模拟每个行人的运动模式
GLSTM:交互的时间相关性
在时间步Tobs处,每个行人的两个LSTM中有两个隐藏变量( m i T o b s , g i T o b s m^{Tobs}_ i,g^{Tobs}_i miTobs,giTobs)
在我们的实现中,这两个变量在连接之前被馈送到两个不同的多层感知器( δ 1 ( ⋅ ) δ1(·) δ1(⋅)和 δ 2 ( ⋅ ) δ2(·) δ2(⋅)):
3.5. Future Trajectory Prediction(未来轨迹预测)
先前的大多数工作[1、33、13]通过学习高斯分布的参数来体现这种不确定性,然后获得从分布中采样的未来位置。
在训练阶段,这些模型在预测的高斯分布下最大程度地降低了真实位置的负对数似然损失。
然而,由于采样过程不可微分,这种方法在反向传播中带来了困难[12]。
Gupta等[12]提出了一种多样性损失,以鼓励网络产生各种样本,并验证了其方法的有效性。我们遵循他们的策略来模拟行人运动的多峰特性。
我们模型的中间状态向量包括三个部分:M-LSTM的隐藏变量,G-LSTM的隐藏变量和添加的噪声(如图2所示)。中间状态向量的计算公式为:
z z z:噪声
h i h_i hi:等式9
中间状态矢量 d i T o b s d^{Tobs}_i diTobs充当解码器LSTM(称为D-LSTM)的初始隐藏状态。预测的相对位置:
W d W_d Wd: D-LSTM权重
δ 3 ( ⋅ ) δ3(·) δ3(⋅):线性层,
e i T o b s e^{Tobs}_i eiTobs :等式 2.
在获得时间步Tobs + 1的预测相对位置后,根据上式根据等式计算D-LSTM的后续输入。
而且很容易将相对位置转换为绝对位置以计算损失。
文献[12]中的损失如下:对于每个行人,模型通过从N(0,1)(标准正态分布)中随机采样z来产生多个预测轨迹。然后,它选择与真值差距最小的轨迹作为模型输出来计算损耗:

Y i Y_i Yi为行人i的ground-truth轨迹,
Y ^ i k \hat{Y}_i^k Y^ik为模型产生的轨迹,k为超参数。
通过只考虑最佳轨迹,这种损失鼓励网络覆盖符合过去轨迹的输出空间。
3.6. Implementation Details
所有LSTM都只有一层
e i t e^t_i eit维数=16
m i t m^t_i mit 公式3中维数=32
图4中,
第一图注意层的形状:16×16
第二层图的形状为:16×32,
第一图关注层 公式4中的a维数=32
第二层=64。
批归一化应用于图关注层的输入
g i t g^t_i git=32
δ ( . ) \delta (.) δ(.)公式7包含3个具有ReLU激活功能的层,隐藏节点=32、64和24
δ 2 ( . ) \delta_2(.) δ2(.):公式8包含3个具有ReLU激活功能的层,隐藏节点的数量=32、64、16
z z z公式10 =16
我们使用Adam优化器以0.01的学习率和64的批量大小训练网络。
4 实验
数据集:ETH 和UCY
评估指标:
1.平均位移误差(ADE):预测轨迹中所有估计位置的均方误差(MSE),以及地面真相轨迹。
2.最终位移误差(FDE):在Tpred处预测的最终目标与真实最终目标之间的距离。
Baselines.
- LSTM:
- S-LSTM:
- Social Attention:
- CIDNN:
- SGAN:
4.1. Quantitative Evaluation(定量评估)
5 结论
在这项工作中,提出了一个新颖的seq2seq框架,该框架可以共同预测场景中所有行人的未来轨迹。我们对每个轨迹使用一个LSTM来捕获每个行人的历史轨迹信息,并采用图注意力网络对每个人群在每个时间步的交互进行建模。此外,采用了另一个LSTM来显式地建模交互之间的时间相关性。在两个可公开获得的数据集上,我们提出的方法优于最新方法。定性实验表明,图注意力网络可以根据邻居的运动状态为邻居赋予合理的重要性,并且我们的模型可以预测不同场景下的准确轨迹。