[论]【ST-MRGNN】Joint Demand Prediction for Multimodal Systems: A Multi-task Multi-relational

Joint Demand Prediction for Multimodal Systems: A Multi-task Multi-relational Spatiotemporal Graph Neural Network Approach

原文链接：见ST-MRGNN
作者：Yuebing Liang, Guan Huang, Zhan Zhao
期刊：Computer Science > Machine Learning
关键字：需求预测·多模态系统·多关系图神经网络·多任务学习·异质时空关系

---

摘要

动态需求预测Dynamic demand prediction对于城市交通系统的有效运营和管理至关重要。人们对单一运输方式的需求预测进行了广泛的研究，但忽略了不同运输方式的需求可以相互关联的事实 ignoring the fact that the demands for different transportation modes can be correlated with each othe。尽管最近做出了一些努力，但现有的多模式需求预测方法通常不够灵活，无法考虑具有不同空间单元和跨不同模式的异构时空相关性的多路网络。为了解决这些问题，本研究提出了一种用于多模式需求预测的多关系时空图神经网络（ST-MRGNN）multi-relational spatiotemporal graph neural network (ST-MRGNN)。具体而言，跨模式的空间依赖性用多个模态内和模态间关系图进行编码。提出了一种多关系图神经网络（MRGNN）来捕获跨模式异构空间依赖，该网络由广义图卷积网络和基于注意的聚合模块组成，前者用于学习关系图中的消息传递机制，后者用于总结不同的关系consisting of generalized graph convolution networks to learn the message passing mechanisms within relation graphs and an attention-based aggregation module to summarize different relations。我们进一步将MRGNS与时间选通卷积层集成，以联合建模异质时空相关性We further integrate MRGNNs with temporal gated convolution layers to jointly model heterogeneous spatiotemporal correlations。使用来自纽约市的真实地铁和叫车数据集进行了大量实验，结果验证了我们提出的方法在不同模式下的性能优于现有方法。对于需求稀少的位置，改进尤其大。对ST-MRGNN注意机制的进一步分析也证明了其对理解跨模式交互的良好解释能力。

1 Introduction

城市交通系统在本质上通常是多模式的，由几个相互连接的子系统组成，代表不同的交通方式，如火车、公共汽车和汽车。它们旨在满足多样化的出行需求，并在服务中断的情况下为城市居民提供多种出行选择。随着城市人口增长、交通基础设施容量有限，以及人们对城市弹性的日益关注，以一体化方式规划、管理和运营多式联运系统比以往任何时候都更加重要。例如，网约车服务可以被智能部署，以帮助人们更好地使用公共交通服务，或者在交通系统过于拥挤或延误时替代某些交通出行。这种多式联运运营策略依赖于对不同运输方式的出行需求进行准确及时的联合预测，这是本研究的重点。重点：多模式运输

随着出行数据的广泛可用和计算技术的快速发展，短期出行需求预测受到了广泛关注，但大多数研究都集中在特定目标模式的需求预测上。虽然早期的方法基于各种回归模型(如ARIMA)，但最近的研究重点是基于深度学习的方法，特别是图神经网络(gnn)，因为它们能够在大规模迁移数据中提取复杂的时空知识[1,2]。尽管预测性能有所改善，但这些方法仍然将目标运输模式视为一个封闭系统，忽略了其与其他模式的潜在相互作用。在实践中，不同的交通方式之间通常通过个体的模式选择、模式间的旅客换乘或出行链活动存在一定的时空相关性。例如，一个地铁站的客流可能会影响该地区的网约车服务的使用，因为旅行者可能会使用网约车作为地铁车站[3]的馈线。因此，一个模态的需求模式很可能可以帮助我们预测另一个模态的未来需求。此外，深入了解多式联运需求的复杂依赖关系，可以帮助我们更好地制定多式联运运营策略，缓解交通拥堵，改善用户体验，增强系统弹性。优势：多模式的需求预测

多式联运需求预测的一个主要挑战是，不同的运输方式有不同的空间单元:一些是基于站点的(如地铁)，而其他的是无站点的(如网约车)。

对于基于站的模式，其操作是站级的，因此需求预测应匹配相同的空间粒度。
对于无站模式，操作人员通常定义一些服务区域作为操作的基本单元。

为了联合建模多式联运需求，最近的研究通常将多式联运需求聚合到一个空间网格[4,5]或其他定义良好的区域分区[6]。基于相同的空间结构，可以对不同的模式执行相似的模型架构来学习共享的时空特征[7]。这些方法通常不太适合基于站的模式，因为一个区域可能包含0个或多个站。针对基于车站的公共交通服务的多模式需求预测，Li等人[8]开发了一个记忆增强的递归模型，用于从车站密集模式到车站稀疏模式的知识适应，尽管它只存储和共享模式级的时间知识，不能利用跨模式的空间依赖。总而言之，尽管进行了广泛的研究，但仍有两个重要的研究空白有待解决:

以往的研究主要集中在单模态需求预测上，只考虑了模态内的时空相关性，而忽略了其与其他模态的潜在相互作用。多式联运关系的存在是因为复杂的旅行行为，可以随着空间和时间的变化，使它们难以建模。
现有的多模态需求预测方法通常需要基于相同区域划分聚合多模态需求数据以实现可共享的特征学习。这些方法无法捕获具有多重网络和不同空间单元的一般多模态系统的跨模态异构时空相关性。

本研究的总体目标是通过开发多任务、多关系的时空图神经网络(ST-MRGNN)方法进行多模态需求预测，以解决上述问题。基于该方法，跨不同模式的不同空间单元(如站点或区域)的空间依赖性通过多个模态内和模态间关系图进行编码，通过广义图卷积网络学习到节点特定表示，并通过基于注意力的聚合模块进行汇总。利用时空块提取数据的异构时空关系。基于来自纽约市的真实多模态数据集进行了实证验证。本研究的具体贡献总结如下:

我们提出 ST-MRGNN ，一种基于图学习的方法用于多模态系统的需求预测。据我们所知，这是第一个在具有不同空间单元的多模态系统中考虑异质时空依赖性的多模态需求预测模型
提出了一种多关系图神经网络(MRGNN)来模拟不同空间单元之间的空间依赖关系。具体地说，通过多模内和多模间关系图编码跨模态依赖关系，利用广义图神经网络学习每个关系图中的消息传递机制，并利用基于注意力的聚合模块对不同关系中的信息进行聚合。
我们引入多关系时空块的设计来联合建模异构空间单元之间的时空相关性。具体来说，每个ST-MR块通过门控卷积层捕获模式特定的时间模式，并融合MRGNN层中的异构时间信息。
基于来自纽约的真实地铁和网约车数据集进行了广泛的实验。结果表明，该方法在不同模式下的性能优于现有方法，且对需求稀疏的位置有较大的改进。

2 Literature Review

在本节中，我们将短期出行需求预测分为单模需求预测和多模需求预测两大类，对现有的短期出行需求预测研究进行综述。此外，我们对异构图嵌入的近期工作做了一个简短的总结，这将与我们提出的模型相关。

2.1 Single-mode Demand Prediction

单模需求预测是一个被广泛研究的问题。早期研究通常基于各种回归模型将出行需求建模为时间序列，包括ARIMA[9]、局部回归[10]、Kalman Filter[11]和Bayesian Inference[12]。例如，Moreira-Matias等人[13]通过将ARIMA与时变泊松模型相结合，开发了一种基于集成学习的出租车需求预测方法。Tong等人[14]提出了一个具有大量特征的线性回归模型来预测出租车需求。然而，这些方法往往不能捕获大尺度移动数据的非线性和复杂依赖性，这可能导致相对较低的预测性能。

---

最近，深度学习受到越来越多的关注，因为它提供了一种新的解决方案来模拟复杂的时空关系。例如，

Lv等[15]将一种堆叠式自编码器模型应用于高速公路系统的交通流预测。
Xu等人[16]设计了 循环神经网络(RNNs) 来学习历史顺序模式，并进行出租车需求预测。

虽然这些方法证明了深度神经网络对需求预测的有效性，但空间信息没有被明确考虑。为了解决这个问题，研究人员使用卷积神经网络(CNNs)通过将研究区域划分为类似图像像素的规则形状的细胞来提取空间相关性。

Ke等人[17]提出了一种按需乘车服务需求预测模型，利用卷积和长短时记忆(Long - term - Memory, LSTM)网络同时捕获时空相关性。
随后在[18]中开发了一个多视角学习框架用于出租车需求预测，该框架融合了CNNs和rnn。
Noursalehi等人[19]引入了一个用于城市轨道系统OD需求预测的时空模型，该模型具有卷积层，以捕获OD矩阵中的空间依赖性。

虽然cnn在欧氏空间(如空间网格)的相关性方面工作得很好，但它们不适用于非欧氏空间，如不规则的服务区域和分布不均匀的中转站。此外，基于cnn的模型只捕获空间上相邻邻居之间的相关性，而对具有类似功能的遥远位置之间的潜在相关性不敏感。

---

为了解决这些问题，图神经网络(GNNs)已成功地应用于交通运输中的各种任务。

Li等人[1]首先提出了扩散图卷积网络(GCNs)，并将其与循环层集成用于交通预测。
Yu等人[20]引入了一种卷积架构用于时空预测，其中GCNs用于捕获空间相关性，而门控cnn用于捕获时间相关性。

这些方法假设空间依赖性是由距离预先决定的，而忽略了具有相似功能或土地利用模式的地点之间的相关性。为了揭示跨移动网络的复杂依赖关系，

Wu等人[21]提出了一种自适应学习技术，通过节点嵌入学习自适应邻接矩阵来捕获隐藏的空间依赖关系。
在[2]中开发了一个多图卷积网络，利用多个图对位置间的成对相关性进行编码。
Li等人[22]提出了一个基于gcn的公共交通需求预测模型，利用需求相似性来确定空间依赖性。
Liang等人[23]提供了一种基于动态图学习的交通数据imputation方法，该方法利用前馈网络从实时交通状况中学习动态空间依赖性。

---

虽然前面提到的方法在需求预测方面都取得了很好的效果，但是它们都是针对单一任务(即单个输出变量)开发的。由于单一变量无法充分描述出行需求，近年来的研究已将重点转向多任务需求预测。

Zhang et al.[24]提出了一种基于lstm的模型来联合预测出租车上落需求。
利用卷积多任务学习网络，在[25]中提出了一个多区域需求预测模型。
Wang等人[7]和Feng等人[12]都引入了一种基于区域和基于出发地目的地的需求值协同预测的时空架构。
在[26]中，将每个区域的需求预测视为一个独立的任务，开发了一种自适应的任务分组策略，用于社区感知的多任务需求预测。

然而，这些多任务模型是为了对同一运输方式的多个需求变量进行联合建模，不能直接适用于多模式需求预测。后者要求模型考虑不同模式间空间结构和需求模式的内在差异。

2.2 Multimodal Demand Prediction

多模态需求预测问题一直没有得到足够的重视。

Y e等[4]结合了CNN和LSTM，共同预测了出租车和共享单车的上车和下车需求。在他们的研究中，研究区域被划分为规则形状的细胞，对出租车和共享单车的需求被聚集到同一个网格中。
同样，Wang et al.[5]提出了一种卷积递归网络，基于相同的空间网格来共同预测网约车和共享单车的出行需求。
在[6]中，引入基于多图学习的方法，对不同服务模式(即单人专车和共享专车)的区域网约车需求进行预测。

总的来说，这些模型都将不同模式的需求数据聚合到同一个分区中。由于多式联运系统往往具有异构的网络结构和多样化的空间单元(如地铁站和网约车区域)，使得联合预测更具挑战性，因此不适合用于一般的多式联运需求预测。一个例外是

[8]，他设计了一种内存增强的循环架构，用于从站点密集模式到站点稀疏模式的知识适应。然而，内存增强网络只能存储和共享模式级的时间知识，不能利用区域/站级的跨模式空间依赖。

本研究旨在开发一个多任务学习框架，用于多模态需求预测，该框架能够从不同网络结构中提取异质空间单元之间复杂的时空相关性。

2.3 Heterogeneous Graph Embedding

虽然已经有大量的GNN体系结构用于由一种类型的节点和边组成的同构图，但它们不适用于由不同类型的节点和边组成的异构图。为了解决这个问题，最近一些研究提出了异构图嵌入的新技术。他们大多集中在信息网络，包括知识图，社交网络和推荐系统[28]。例如

Schlichtkrull等[29]引入关系GCNs来处理不同实体的知识图，并将其应用于链接预测和实体分类任务。
在[30]中提出了一种基于组合的GCN，它将节点和关系共同嵌入到一个图中。

为了了解相邻节点间异质性的重要性，注意机制在近年来的研究中得到了应用。例如，

Wang等人[31]利用分层注意机制(包括节点级注意和语义级注意)捕获跨书目网络的异构语义信息。
同样，Zhang等[32]针对知识图完成任务提出了一个两级注意的GNN:第一级注意编码关系级重要性，第二级注意编码实体级重要性。

然而，这些研究都是针对信息网络以及相关的任务，如节点分类、链路预测、图完成等。很少有研究研究异质性流动网络，这是更具挑战性的两个原因。

首先，虽然信息网络通常有预定义的边/关系，但跨移动网络节点之间的相关性更复杂，没有定义良好。
其次，与大多数信息网络不同的是，移动网络会随着时间的推移而动态变化，这是由于拥堵、服务可用性和人类活动的结果，因此在考虑空间维度的同时，还应考虑时间维度。

本研究引入多关系时空图神经网络，可有效解决上述问题。

3 Methodology

在本节中，我们首先定义几个重要的概念并阐明我们的问题。接下来，我们引入了一种新的多模态需求预测的时空建模框架，该框架将多关系图神经网络( MRGNN s)与时间卷积网络(TCNs)结合起来，共同建模跨多模态的异构时空相关性。

3.1 Definitions and Problem Statement

多模式交通系统

$X^t=\{X_m^t,m=1,2,\cdots ,k\}$,$t$表示时间，$m$表示交通方式，$X_m^t\in R^{N_m\times 2}$,$N_m$指的是mode为$m$的顶点的个数，2指的是每个顶点的特征维度。

模内关系图和模间关系图

• 模内关系图：$G_{intra}=\{G_m,m=1,2,\cdots ,k\}$,$G_m=(V_m,A_m)$表示mode 为$m$ 的图关系
• 模间关系图：$G_{inter}=\{G_{mn},m,n=1,2,\cdots ,k\}$,$G_{mn}=(V_m,V_n,A_{mn})$表示mode 为$m$的顶点集合$V_m$和mode 为$n$的顶点集合$V_n$之间的图关系
  

多式联运需求预测问题

Problem多式联运需求预测问题(Multimodal Demand Prediction):
基于多式联运需求的历史观测数据，以及多式联运和多式联运的关系图，多式联运需求预测问题的目的是联合预测下一个时间区间内所有运输方式的需求。其中，给定两种模式$m$和$n$的历史观测值为$X_m^{t-T}$、$X_n^{t-T}$，模型内关系图$G_m$、$G_n$和模型间关系图$G_{mn}$得到一个映射函数$F(\ast )$，共同预测$t+1$时刻所有运输模式的需求，记为$X^{t+1}$，给定为:

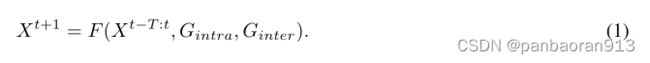
虽然问题是一般性的，但我们将只关注地铁和网约车的双峰系统作为案例研究，以演示我们的实验中提出的模型(见第4节)。为了突出异质性空间单元的问题，地铁被选为基于站点的模式的例子，网约车被选为无站点模式的例子。在这种情况下，k = 2，定义了3个关系图 relation graphs来编码跨模态相关性，包括2个模内图intra-modal graphs和1个模间图 inter-modal graph。

3.2 Network Architecture

让我们首先介绍我们提出的模型的总体框架。如图1所示，ST-MRGNN由L个多关系时空块(ST-MR块)组成，用于揭示跨多个模态的异构时空模式，每个模态都有一个输出层用于生成最终的预测结果。每个ST-MR块由多个门控卷积层(TCNs)和一个多关系图神经网络(MRGNN)组成，分别捕获时间特征和空间特征。具体来说，在每个ST-MR块中，首先对每个模式应用一个单独的TCN层，以捕获模式特定的时间模式。然后将提取的TCN层模式特征融合到MRGNN层中，对每个模式的异构时空依赖性进行联合建模。在MRGNN层之后是另一个模式特定的TCN层，因为通过实验我们发现它有助于提高预测性能。这可能是因为这种“三明治”结构可以通过TCN层[20]促进图卷积之间的快速空间-状态传播。下面介绍每个模块的详细信息。

Fig.1 ST-MRGNN的结构(⊕表示剩余连接)

3.3 Multi-relational Graph Neural Network

在本节中，我们介绍了一种新的图神经网络MRGNN，它能够捕获跨多种模式的节点之间的异构空间依赖关系。为了阐述MRGNN的关键思想，我们在图2中给出了一个用于双峰运输系统的MRGNN框架。MRGNN由三个主要部分组成:(1)空间依赖建模:对每个关系图考虑两种类型的空间依赖，即地理邻近性和功能相似性;(2)模内和模间图卷积:引入广义GCN对模内和模间关系图的节点级邻域信息进行聚合;(3)关系聚合:设计基于注意力的聚合模块，对不同关系中聚合的特征进行聚合。下面将详细描述这三个部分。

Fig.2 MRGNN的双峰框架

3.3.1 Spatial Dependency Modeling

先前的研究表明，空间依赖不仅存在于空间上相邻的位置之间，也存在于功能相似、环境相似的距离较远的位置[2]。为了捕捉位置之间的地理和功能相关性，我们为每个图编码了两种类型的空间依赖性:
Geographical Proximity（地理上的接近）:地理上相互接近的位置可能显示出很强的相关性。我们使用基于距离的邻接矩阵$A_G$对节点之间的地理关系进行编码。形式上，有了每个区域和站的地理中心，我们可以计算$A_G$为:

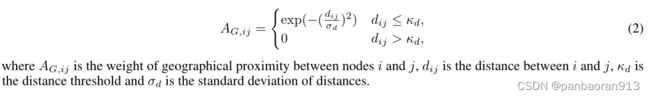
Functional Similarity(功能相似性) :显示相似需求模式的位置也可能共享一些共同的功能或其他上下文特性。为了获取这种语义关联，我们为每个图构造一个邻接矩阵$A_P$。为了处理不同模式的需求变化，我们首先对各模式的需求序列进行归一化，$A_P$为:

一般来说，对于每个关系图，我们可以为$u$种空间依赖关系建模。因此，在一个多模态系统M中，总共有$u\times (k+C_K^2)$关系可以编码，包括$u\times k$模内关系和$u\times C_2^k$方式的关系。注意，这是模型中需要考虑的最大关系数量，并不是所有的关系都是必要的，这取决于系统配置和需求模式。在我们的例子中，k = 2, u = 2，有4个模内关系和2个多模间关系。图3展示了一个包含地铁和网约车的多式联运系统的示例。实线和虚线用于区分基于地理邻近或功能相似性的空间依赖性。线的颜色用来区分交叉模态关系。

Fig.3 多模态系统的空间依赖性建模

3.3.2 Intra-modal and Inter-modal Graph Convolutions

基于3.3.1节介绍的多关系图，每个节点通过多个$(u\times k)$关系从多个$(k)$模式连接到异构节点[ each node is connected to heterogeneous nodes from multiple (k) modes via multiple (u × k) relations]。使用图卷积可以很自然地从每个关系中聚合连接节点的特征。然而，大多数的gcn是针对具有方阵邻接矩阵的图结构开发的，不能应用于具有异质节点和非方阵邻接矩阵的多式关系图。为了解决这个问题，我们引入了广义图卷积网络(GGCN)，它是[33]中提出的标准GCN的扩展。回想一下，MRGNN的输入是从TCN层学习到的模式特定的时间特征。给定一个多模态关系图$G_{mn}=(V_m,V_n,A_{mn})$，从TCN层中提取特征$H_m\in R^{Nm\times c_{in}^s}$, $H_n\in R^{Nm\times c_{in}^s}$，则定义图卷积层为:

正如3.3.1节所介绍的，每个图都可以用$u$个类型的空间依赖性编码。为了同时处理一个图上的多个依赖项，我们将GGCN扩展到多维张量，给定为

当$m=n$时，模内关系图( intra-modal relation graph)可以看作是多模态关系图的特例，因此，给定模态$m$及其模内关系图$G_m=(V_m,A_m)$，模态m节点间的相关性建模为:


通过模内和模间图卷积，每个节点接收来自其异构邻域节点的$u\times k$聚合特征向量。给定模式$m$中的节点$i$，表示其聚合特征的集合为:

从上看公式得知，就是普通GCN,只是矩阵的搭建方式不同罢了

3.3.3 Relation Aggregation

对于每个节点，从不同的关系中总结学习到的特征，一个直观的操作是简单的相加。但是，不同关系对不同节点的贡献可能不同。例如，靠近地铁站的网约车区域可能很容易受到多式联运关系的影响，而距离任何地铁站较远的网约车区域可能更依赖于多式联运关系。为了捕捉这种变化，我们设计了一个关系级注意模块 a relation-level attention module来学习每个关系对目标节点的贡献。给定$m$模式下的节点$i$，注意模块的表达式为:

3.4 Temporal Convolution Layer

我们采用[20]中提出的时间卷积网络(TCN)来捕获多模态系统中节点的时间模式。与时间序列分析中广泛使用的基于rnn的模型相比，cnn具有训练时间快、结构简单等优点。给定一个节点的输入序列，时间卷积层使用带有$K_t$大小核的1-D因果卷积来建模每个时间步与其$K_t$邻域之间的相关性。[20]之后进行卷积层，没有填充，因此每次输出序列长度缩短$K_{t-1}$。

先前的研究表明，门控机制对于RNN和temperal CNNs[21]的时间建模都是至关重要的。为了控制通过层的信息的比例，在卷积层中加入一个输出门。数学上，给定模式为$m$的节点$i$及其输入序列$h_{in,i}^{(m)}$，时间门控卷积的形式为:

3.5 Multi-relational Spatiotemporal Block

为了整合空间和时间域的相关性，我们将MRGNN和TCN合并到ST-MR块中。每个ST-MR块由两个TCN层和一个MRGNN层组成。第一个ST-MR区块的输入是历史的多模态需求序列。在实现中，对每个时间步并行应用一个相等的MRGNN层。同样，通过对每个节点使用相同的卷积核，将TCN层推广到3D张量。为了提高训练速度，我们在TCN层之间采用残差连接[34]，设为:


回想一下，历史需求序列的输入长度为$T$，每过一层$TCN$，序列长度就缩短$K_{t-1}$。堆叠L个ST-MR块后，ST-MR块的输出序列长度缩短为$T-L\times (K_t-1)\times 2$。如果输出序列仍然大于1，则为每个模式附加额外的TCN层，以将输出降阶到单个时间步。输出层是一个前馈网络，它将ST-MR块的输出信号映射到每个模式的预测结果。

3.6 Training Strategy

该模型的训练目标是在所有模态的所有节点上最小化真实需求与预测需求之间的差异。损失函数定义为:

4 Experiments

4.1 Data Description
为了验证我们提出的模型的有效性，我们在纽约市的真实多模态数据集上进行了实验。具体来说，我们将地铁作为基于车站的模式的一个示例，将叫车作为无车站模式的一个示例。我们之所以选择这两个数据集，是因为之前的研究表明，地铁和网约车都是城市交通系统的重要组成部分，并表现出很强的时空相关性，尤其是在大都市地区[3]。在本研究中，我们以曼哈顿为研究区域，数据收集时间为2018年3月1日至2018年8月31日。

纽约地铁NYC Subway (https://toddwschneider.com/dashboards/nyc-subway-turnstiles)2:该数据每4小时提供纽约地铁站转门的使用次数。在我们的研究区域的136个地铁站，共有2,289个旋转门用作出入境登记。在研究期间，平均每天大约有240万条目/存在计数。原始数据包括车站ID、转门ID、记录时间、条目和存在计数等信息。

纽约市打车服务NYC Ride-hailing3 https://www1.nyc.gov/site/tlc/about/tlc-trip-record-data.page:纽约市出租车和豪华轿车委员会(TLC)提供的租车车辆数据是基于优步和Lyft等叫车公司的数据。它包括研究期间的4300万次出行记录，平均每天23.4万次。每次行程，数据提供以下信息:上车时间、上车区域、下车时间、下车区域等。层位由薄层色谱(TLC)预先确定。本研究区域共有63个TLC层.

纽约市多模态数据的空间分布和时间格局如图4和5所示。从图4可以清楚地看出，不同出行方式的空间单元具有异质性，地铁以站点为基础，网约车以区域为基础。地铁和网约车的需求呈现出相关的空间分布:需求最密集的站点/区域主要在曼哈顿中城，其次是市中心，最后是上城。图5对比了不同模式下每个站/区域每4小时的平均需求密度。显然，地铁的出行需求比网约车大得多。二者的需求模式也存在时间相关性，但地铁需求表现出更明显的通勤模式。由于许多纽约Y型工人居住在郊区，通勤到曼哈顿工作，我们可以看到地铁流出的高峰在下午，而地铁流入的高峰在上午更高。

Fig.4 曼哈顿地区多式联运需求的空间分布

Fig.5 曼哈顿多式联运需求的时间模式

4.2 Baseline Models

正如2.2节所介绍的，现有的大多数多模态需求预测方法要求需求聚集在同一个分区上，不适合具有不同空间单元的多模态系统。唯一的例外是[8]，他提出了一个记忆增强的递归模型，用于从站点密集模式到站点稀疏模式的知识适应。因为源代码是不可用的，所以我们不能复制相同的模型，而且我们自己的实现也不能像其他基线那样执行得好。因此，我们只给出单模预测方法的基线结果如下:

• 历史平均 Historical A verage (HA):一种统计方法，用以前时间步的平均值预测未来的需求。
• 线性回归Linear Regression (LR)：一种建模未来需求和历史时间序列之间关系的回归方法。
• eXtreme Gradient Boosting (XGBoost)[36]:一种基于梯度Boosting决策树的代表性机器学习方法。
• Long-short Term Memory (LSTM)[16]:深度学习模型，将LSTM与前馈网络相结合，用于时间序列建模。
• Spatiotemporal Graph Convolution Network (STGCN)[20]:一种基于gcn的方法，用基于光谱的GCNs建模空间相关性，用时间卷积层建模时间相关性。
• Multi-graph Convolution Network (MGCN):一个多图卷积网络，通过多个gcn捕捉多种类型的空间相关性，并通过上下文rnn捕捉时间相关性。
• Graph WaveNet[21]:一种时空图学习方法，使用自学习邻接矩阵，通过节点嵌入捕获复杂的空间相关性。

4.3 Experiment Settings

为了对齐不同的数据集，我们将多模式需求数据聚合为4小时间隔，并对每个模式应用最小-最大归一化。我们选择4小时间隔，因为纽约地铁需求数据也是每4小时汇总一次。设定历史时间步长T为6(即6 × 4 = 24小时)。对于所有的深度学习模型，我们使用前60%时间步骤的数据进行训练，后20%时间步骤的数据进行验证，最后20%时间步骤的数据进行测试。设置训练epoch的数量E为500，我们在验证集上使用早期停止来防止过拟合。模型使用Adam Optimizer进行训练，学习率为0.002，批处理大小为32，dropout为0.3,L2正则化，权重衰减等于1e-5。

通过大量实验，我们确定了我们所提出的模型的超参数如下:ST-MR块的数量L = 2，时间卷积核的宽度Kt = 2, TCN层的输入和输出维数$c_{in}^t=16,c_{out}^t=64$, MRGNN层的输入和输出维数$c_{in}^s=64,c_{out}^s=16$，输出层的隐藏维数$c_h=128$。地铁、网约车的损失平衡超参数${\epsilon }_m$分别设为0.5、0.5。 对于基线模型，我们自己实现XGBoost和LSTM，并根据验证集微调其超参数。对于STGCN和Graph WaveNet，我们使用原始作者提供的带有默认参数设置的开源代码。对于MGCN，原来的性能较差，因此我们通过实验，为每一个关联添加额外的GCN层。这些模型是用测试集上计算的三个常用度量来评估的:均方根误差(RMSE)、平均绝对误差(MAE)和决定系数(R2).

5 Results

5.1 Comparison of Model Performance

表1总结了不同模型对纽约市地铁和网约车的需求预测效果。每个模型运行10次，并报告平均值。对于所有车型，地铁的RMSE都要比网约车大得多。这是因为纽约的地铁出行比网约车要多得多。地铁也与更高的R2相关，表明地铁比网约车有更规则和可预测的需求模式。与基线模型相比，我们提出的模型ST-MRGNN在跨模式的所有评估指标上都取得了最好的性能，这表明两种模式都可以受益于其他模式的需求模式的知识。

Tab.1 NYC Dataset上不同模型的性能比较

在基线模型中，HA和LR的表现较差，表明经典统计模型在提取非线性时空相关性方面存在局限性。XGBoost对网约车需求的预测性能较差，但与LSTM对地铁的预测性能相当，这说明集成方法在某些情况下是有效的。在深度学习模型中，LSTM的性能较差，说明需要考虑需求预测的空间依赖性。 MGCN在地铁和网约车方面的表现优于STGCN，显示了考虑多种类型空间依赖的价值。得益于自适应邻接矩阵，Graph WaveNe实现了两种模式的竞争结果。我们提出的模型实现了比Graph WaveNet更好的预测性能，地铁的RMSE和MAE提高了5.04%和11.49%，网约车的RMSE和MAE提高了12.98%和15.05%。现有模型大多只考虑模态间的依赖关系，而ST-MRGNN可以有效地解释模态间复杂的时空关系。与RMSE和MAE相比，我们的模型在R2上的相对改进相对较小，但仍然显著。

为了直观地说明需求预测结果，我们比较测试集的前四周的平均预测值和真实值。如图6所示，预测曲线(橙色)可以准确地跟踪实际曲线(蓝色)。具体而言，地铁需求表现出较强的时间周期性，而网约车需求表现出较多的不规则波动，这可能是因为人们使用网约车不仅是为了上下班，还可以用于各种不同的目的(如休闲)，这些目的的时空规律性较小。因此，网约车需求更难预测，R2较低就是证明。与此同时，我们提出的模型可以实现对网约车的更好的预测性能，因为它的一些需求不规则性可以通过多关系的内部和多式联运依赖来解释.

Fig.6 2018-07-25 ~ 2018-08-22期间的平均预测值和真实值

图7在10次运行的基础上比较了几个选定模型的稳定性。我们发现我们的方法在大多数情况下具有最好的性能，性能变化相对较小。对于网约车需求预测，我们提出的模型几乎在所有实验中都明显优于Graph WaveNet。对于地铁需求预测，在75%以上的实验中，ST-MRGNN的均方根误差最小。在基线模型中，MGCN的模型稳定性较差。这可能是因为它采用了一种模型结构，在这种结构中，不同类型的关联用单独的GCN层并行建模。与MGCN不同的是，ST-MRGNN和Graph WaveNet都使用带有GCN层的堆叠时空块来编码空间相关性，增强了不同块之间的相互联系，提高了模型的稳定性。

Fig.7 模型稳定性比较

我们还比较了STGCN、MGCN、Graph WaveNet和ST-MRGNN的计算成本，如表2所示。结果表明，STGCN模型由于结构简单，在四种模型中效率最高。ST-MRGNN的运行速度是Graph WaveNet的两倍，在训练方面与MGCN相似。对于推断，我们测量测试集上每个模型的总时间成本。ST-MRGNN比Graph WaveNet和MGCN都要快得多。这可能是因为我们的模型同时评估两种模态，而其他模型分别评估不同的模态。这些结果表明，我们提出的模型能够以较低的计算成本获得更准确的预测性能。

Tab.2 计算效率的比较

5.2 Comparison of Model Variants

为了量化不同成分在ST-MRGNN中的作用，我们进一步实施了四种简化版本的ST-MRGNN消融试验。每个变体模型都有一个ST-MRGNN成分，如下所示:

• Inter-modal relation graphs (InterGraph):为了比较有或没有多模态关系图的模型性能，我们实现了一个单模态ST-MRGNN版本，它只使用模内关系图分别建模每个模态。
• Geographical proximity ($A_G$): ST-MRGNN编码两种类型的空间依赖:地理邻近性和功能相似性。随着地理邻近性的减弱，变异模型只使用功能相似性来编码空间依赖性。
• Functional similarity ($A_P$ ):在该变体中，随着功能相似度的依赖性减弱，节点之间的空间相关性仅基于地理邻近进行编码。
• Attention-based aggregation module (AttnAgg):没有注意模块，变量模型通过简单的相加来聚合不同关系的输出。

表3显示了ST-MRGNN及其变型模型在不同模型成分消融后的性能比较。我们发现，由模型中的多模式关系图捕获的跨模式依赖关系对两个数据集的性能改进至关重要。在没有跨模式依赖的情况下，地铁和网约车的RMSE分别增长了8.34%和4.85%。这表明，地理位置附近或功能相似的地铁站和网约车区域的多式联运关系确实有助于彼此的需求预测。同样值得注意的是，对于网约车需求预测，ST-MRGNN的单模版本已经优于表1中列出的基线模型。这表明，对于单一的无站模式(即我们的网约车)，我们提出的模型结构由叠加的时空块和多关系图组成，在提取模态内时空相关性方面已经显示出优势。去除地理邻近性或功能相似性的空间依赖性会导致两种模式的性能下降，验证了考虑这两种依赖性的重要性。两者之间，功能相似度对地铁和网约车需求预测的影响均较大，说明功能相似的站点/区域对不同交通方式的需求预测贡献较大。去除注意力模块后，地铁的RMSE增加了3.71%，网约车的RMSE略有增加，说明注意力机制有助于找到不同模式之间关系的最优组合，尤其是地铁。

Tab.3 不同ST-MRGNN成分的消融分析

5.3 Comparison of Multimodal and Single-mode ST-MRGNN

Tab.4 需求密集站与需求稀疏站的性能比较 为了进一步研究多式联运关系对模型性能的影响，我们将 ST-MRGNN与单式版本的ST-MRGNN(命名为S-ST-MRGNN)进行比较，并检查跨站/区域的差异。如5.2节所述，S-ST-MRGNN的网络结构与ST-MRGNN类似。唯一不同的是，S-ST-MRGNN对各模态分别建模，没有多模态关系。 我们首先将每种模式的站点/区域按照其需求密度级别划分为不同的组。具体而言，根据平均需求水平对地铁站或叫车区进行分类，然后将前1/3的位置划分为需求密集型（DI）位置，将后1/3的位置划分为需求稀疏型（DS）位置. 表4总结了S-ST-MRGNN和ST-MRGNN对DI和DS位置的需求预测效果。显然，对于两种模式，DI位置的RMSE都要远远大于DS位置，这是合理的，因为DI位置具有更高的需求密度。DI位置也与较高的R2相关。与RMSE不同，R2是标准化和无标度的。因此， 研究结果表明，需求较稀疏的地铁站或网约车区域的可预测性较低。它们可能与需求模式中更多的不确定性有关，因此更难以以高可信度进行估计。与S-ST-MRGNN相比，ST-MRGNN在不同站位/区域，尤其是DS站位的表现更好。这意味着DS位置可以从其他模式的需求模式知识中获益更多。在两种模式中，使用S-ST-MRGNN时，DS地铁站的R2远低于DS网约车区域，这可能是因为不同地铁站的需求密度比网约车区域变化更大(见 图4)。同时，使用ST-MRGNN时，DS地铁站的R2相对改善程度远高于DS网约车区域。 图8进一步说明了每个站/区ST-MRGNN相对于S-ST-MRGNN的RMSE改善情况。在地铁方面，ST-MRGNN在大多数站点表现优于S-ST-MRGNN，尤其是在曼哈顿中城和下城( 图8a中的红色和橙色点)。对于网约车，在曼哈顿不同地区的大多数网约车区域的预测性能都得到了显著提高( 图8b中的红色和橙色方块)。这表明多式联运关系可以帮助提高大部分地点的预测性能。

Fig.8 ST-MRGNN相对于S-ST-MRGNN的RMSE改善分布

5.4 Spatiotemporal Analysis of Cross-Mode Dependencies

在本节中，我们将通过关系聚合模块进一步探讨跨模式依赖关系，该模块用于总结给定模式下的每个节点(站点/区域)在跨另一模式的所有其他节点上的时空依赖关系。具体来说，我们考虑u = 2种类型的空间依赖，即在我们的模型中，地理邻近性(基于距离)和功能相似性(基于语义)。因此，对于一个模态的每个节点，有4个估计的注意值，即基于模态内距离的依赖关系、基于模态内语义的依赖关系、基于模态间距离的依赖关系和基于模态间语义的依赖关系。4个注意力值表示节点在预测需求时关注的信息权重，它们的总和为1。

估计的注意力权重的时空分布如图9所示。为了简单起见，与一个模式相关的基于距离和基于语义的依赖被加在一起，同时，当内部依赖和多式依赖的值之和为1时，只给出多式依赖。第一行显示了网约车区域在一天的不同时间对其他地铁站的依赖程度，第二行则相反。颜色代表关注权重值。浅黄色表示在0.5附近的多式依赖值，这意味着多式依赖和多式依赖的权重大致相等。接近红色的颜色表示站点/区域更多地依赖于多模式依赖，而蓝色表示更多地依赖于多模式依赖。从图中我们可以发现，对于网约车和地铁的需求预测都能从多式联运关系中获得显著的收益，有相当多的站点/区域多式联运注意权值大于0.5。对于网约车来说，跨越中城、上城和曼哈顿上城的几个区域从下午高峰时间(16:00)到上午高峰时间(12:00)的多式联运中受益更多，尤其是曼哈顿东北部的东哈莱姆地区。相比之下，在打车需求相对密集、地铁需求相对不高的Downtown和Upper Manhattan北部地区，intra-modal dependency较高。相应的，这些地区的地铁站主要依靠网约车的需求，而不是其他地铁站来为其需求预测提供信息。在午夜至早高峰时段(0:00 - 8:00)，几乎所有地铁站的联运依赖都更为重要。在白天，随着地铁使用的活跃(图5)，多式联运依赖的权重下降，在16:00左右达到最低水平，这是曼哈顿地铁需求的典型高峰时段。

Fig.9 需求预测中模态相关性的时空分布

我们进一步选择时代广场/剧院区网约车区域和时代广场-42街地铁站作为例子，研究它们的需求如何依赖于双峰系统中的其他节点。回想一下，每个关系的节点之间的空间依赖关系是用相应的邻接矩阵编码的。因此，特定关系的节点到节点的依赖关系可以计算为关系级注意权与邻接矩阵中归一化相关权的乘积。图10展示了每个空间依赖关系中节点到节点依赖值最高的前3个邻域节点。很明显，基于距离的依赖(如蓝色虚线所示)主要来自预期的附近区域/站点，但基于语义的依赖(如红色虚线所示)可能来自很远的位置。就相对重要性而言，基于行程的模式内依赖关系比基于行程的模式间依赖关系对所选站点/区域的需求预测更有用，这可能是由于出行需求分布具有显著的空间聚类效应。然而，基于语义的多式联运依赖关系的重要性各不相同，因为它们对所选地铁站更重要，但对网约车区域不那么重要。这些例子证明了我们所提出的模型的可用性，可以在单个站点/区域层面获得操作洞察。

Fig.10 一个网约车区域和地铁站及其跨模式的节点级依赖的例子

6 Conclusion

本文研究了多式联运系统的联合需求预测问题，该问题对于动态提供智能出行建议、减少拥堵、增强系统弹性具有重要意义。与单模需求预测相比，由于不同的运输方式可能具有不同的空间单元和不同的时空相关性，该问题更具挑战性。为了解决这些挑战，我们提出了一种多关系时空图神经网络(ST-MRGNN)方法。具体地说，开发了一个多关系图神经网络(MRGNN)来捕获跨模式异构空间依赖，该网络由三个步骤组成。
首先，不同模态关联节点之间的地理依赖和语义空间依赖被编码为多个模态内和模态间关系图。
其次，引入一种广义图卷积网络，通过每个节点之间的关系，根据其邻域节点来学习每个节点的潜在表示。
第三，我们设计了一个基于注意力的聚合模块，以获得不同关系的最优组合。为了进一步整合空间和时间域的相关性，我们在堆叠的多关系时空(ST-MR)块中加入了MRGNN层和时间门控卷积层，共同建模异构时空相关性。
为了测试模型的性能，我们对来自纽约的真实地铁和网约车数据集进行了广泛的实验。结果表明：
（1）我们提出的模型能够提高地铁和叫车服务的需求预测性能，优于经典和最先进的需求预测方法；
（2） 在我们的模型中，用多个模态间关系图编码的跨模态关系对于提高预测性能至关重要；（3）进一步的分析表明，跨模式关系对于需求稀疏的位置尤其有用。
此外，我们还可视化了从注意机制中学习到的不同关系的时空分布，并证明了我们提出的模型的潜在可解释性。

总之，本研究为如何将图神经网络应用于异质移动性网络以进行多模态需求预测提供了思路。该模型可以通过多种方式进一步改进或扩展。
首先，当关系数量较大时，大多数异构图嵌入技术，包括我们的方法，都可能存在过度参数化的问题。未来的研究可以通过图嵌入[30]等技术来缓解这一问题，提高模型的可扩展性。
其次，不同的运输方式可能有不同的数据分布，在不同的运输方式存在分布差异的情况下，单纯使用多式联运关系可能不是最好的方法。未来的研究可以在模型中加入域适应技术，以促进跨模式的正向迁移。
最后，虽然我们提出的模型是为多模态需求预测而开发的，但它可以很容易地适用于其他研究问题。
例如，如第5.3节所示，由于我们的模型在需求稀疏的位置显示出更多的优势，因此很自然地会调整我们的模型以专门改进通过转移学习，借助需求密集型模式（如地铁），预测需求稀疏模式（如自行车共享）的性能.

---