ViT (Visual Transformer)

Acknowledge

论文名称： An Image Is Worth 16x16 Words: Transformers For Image Recognition At Scale
原论文对应源码：https://github.com/google-research/vision_transformer
PyTorch实现代码： pytorch_classification/vision_transformer
Tensorflow2实现代码：tensorflow_classification/vision_transformer
在bilibili上的视频讲解：https://www.bilibili.com/video/BV1Jh411Y7WQ
博客讲解：https://blog.csdn.net/qq_37541097/article/details/118242600

该文基于霹雳吧啦Wz讲解的Transformer，在此基础上进行一定的扩充，推荐阅读原版。

引言

Transformer最初提出是针对NLP领域的，并且在NLP领域大获成功。这篇论文也是受到其启发，尝试将Transformer应用到CV领域。通过文章的实验，给出的最佳模型在ImageNet1K上能够达到88.55%的准确率（先在Google自家的JFT数据集上进行了预训练），说明Transformer在CV领域确实是有效的，而且效果还挺惊人。

2. 模型详解

在这篇文章中，作者主要拿ResNet、ViT（纯Transformer模型）以及Hybrid（卷积和Transformer混合模型）三个模型进行比较，所以本博文还会简单聊聊Hybrid模型。

2.1 Vision Transformer模型概况

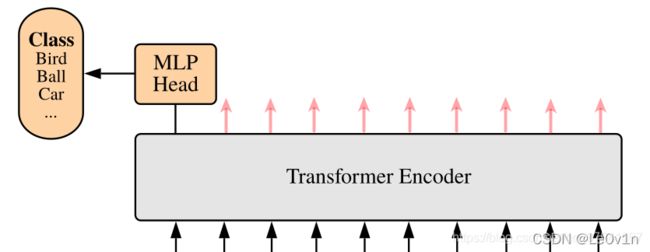
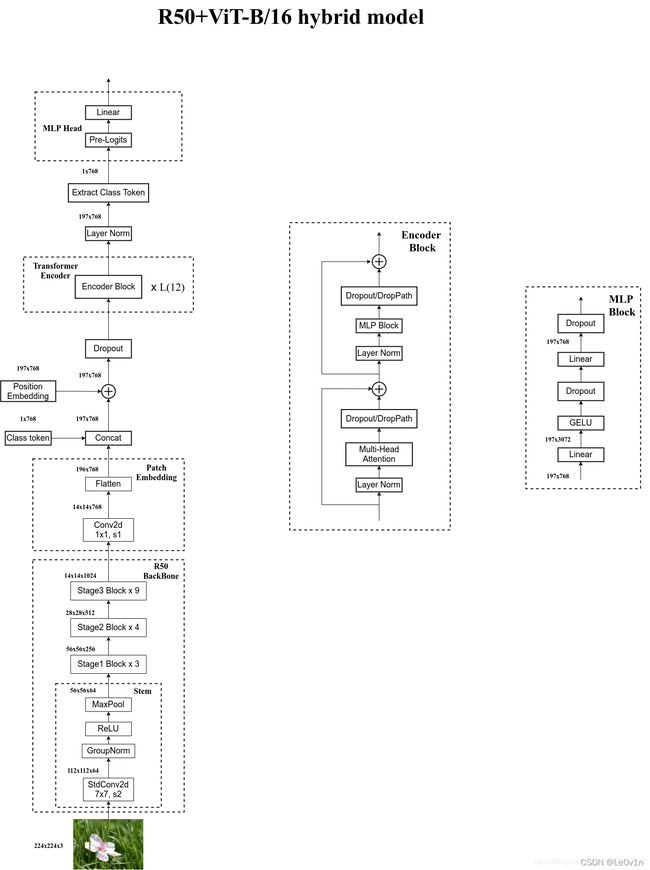
下图是原论文中给出的关于Vision Transformer(ViT)的模型框架。简单而言，模型由三个模块组成：

• Linear Projection of Flattened Patches(Embedding层，也叫作嵌入层)
• Transformer Encoder(编码层，图右侧有给出更加详细的结构)
• MLP Head（多层感知机头，用于最终分类的层结构）

以上ViT的模型架构。网络的工作大致流程如下：

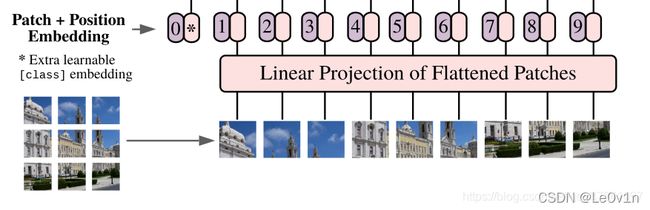
1. 首先输入一张图片，对其进行分成一个一个的patch。
2. 之后对每一个patch输入到Linear Projection of Flattened Patches层（也就是Embedding层）。通过这个Embedding层之后我们就可以得到一个个的向量。这里的向量我们通常称之为token。每个patch通过Embedding层都会得到一个token。
3. 在这一系列token的最前面加上一个新的token（专门用于分类的class token）。
4. 为了让每一个token考虑到位置信息，还需要对每一个token加上位置信息，即Position Embedding。对应图中的0,1,2,3,4,5,6,7,8,9。
5. 将Embedding完的token输入到Transformer Encoder中。Transformer Encoder对应的是右边这张图。在Visual Transformer中，将Transformer Encoder重复堆叠 $L$ 次。
6. 因为我们的网络是用来分类的，所以我们仅仅需要将之前嵌入的class token取出来即可。
7. 将class token送入MLP Head得到最终的分类结果。

2.2 Embedding层结构详解

对于标准的Transformer模块，要求输入的是token（向量）序列，即二维矩阵[num_token, token_dim]，如下图，token0-9对应的都是向量，以ViT-B/16为例，每个token向量长度为768。

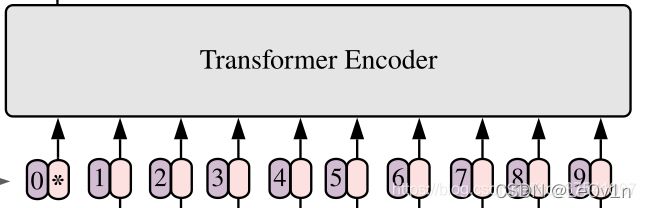
ViT-B/16中：

• ViT: Visual Transformer
• B: Base
• 16: Patch Size, 16×16

2.2.1 Patch Embedding层

对于图像数据而言，其数据格式为 $[H,W,C]$ 是三维矩阵，明显不是Transformer想要的。所以需要先通过一个Embedding层来对数据做个变换。

如下图所示，首先将一张图片按给定大小分成一堆Patches。以ViT-B/16为例，将输入图片( $224\times 224$ )按照 $16\times 16$ 大小的Patch进行划分，划分后会得到 $(224/16{)}^2=14\times 14=196$ 个Patches。接着通过线性映射(Linear Projection)将每个Patch映射到一维向量中，以ViT-B/16为例，每个patch的shape为 $[16,16,3]$ ，通过映射得到一个长度为768的向量（后面都直接称为token）。整体过程为：

$$\underset{\mathrm{I}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{s}}{[224,224,3]}\to \underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{s}}{\underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{n}\mathrm{u}\mathrm{m}}{196}\times \underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}{[16,16,3]}}\to \underset{\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}{\underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{n}\mathrm{u}\mathrm{m}}{196}\times \underset{\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}}{[768]}}$$

Note: patch, patches, token, tokens

1. patch: 根据Patch Size得到的单独的patch，上面示例中的 $[\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e},\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e},\mathrm{C}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{l}]=[16,16,3]$ 就是patch

2. patches: [patch总个数，patch]，就是上面的 $[196,16,16,3]=[(224/16{)}^2,16,16,3]$

3. token: 一维向量，就是单独一个patch映射得到的一维向量，上面示例中的 $[768]$ 就是token

4. tokens: [patch个数, token]，就是上面的 $[196,768]$

---

patches和tokens的区别：其实展平都是一样的，只不过是用不同的shape表示不同的含义罢了
顾名思义，patch意思为小块，我们就将其理解为是特征图，所以是$[16,16,3]$，而token这里我们理解为是一维序列就行，所以它的形状理所当然是$[16\times 16\times 3]=[768]$

在代码实现中，这个过程是直接通过一个卷积层来实现。 以ViT-B/16为例，直接使用nn.conv2d(in_channels=224, out_channels=768, kernel=(16, 16), stride=16)来实现，即：

$$\underset{\mathrm{I}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{s}}{[224,224,3]}\to \underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{s}/\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}{[\underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{n}\mathrm{u}\mathrm{m}}{14,14},\underset{\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}}{768}]}$$

输入输出就不用说了，这里比较巧妙的是kernel=(16, 16)，其实明白卷积是怎么运算的，也很好理解。

然后把 $H,W$ 两个维度展平即可。 $[14,14,768]\to \underset{\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}{[196,768]}$，此时正好变成了一个二维矩阵，正是Transformer想要的。

$$\underset{\mathrm{I}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{s}}{[224,224,3]}\to \underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{s}}{[14,14,768]}\to \underset{\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}{[196,768]}$$

2.2.2 Class Embedding 层

注意：在输入Transformer Encoder之前需要加上

• [class]token → 接下来会说的
• Position Embedding → 2.2.3会说

在原论文中，作者说参考BERT，在刚刚得到的一堆tokens中插入一个专门用于分类的[class]token，这个[class]token是一个可训练的参数，数据格式和其他token一样都是一个向量。

以ViT-B/16为例，就是一个长度为768的向量，与之前从图片中生成的tokens $[196,768]$ 拼接在一起，即：

$$\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}([1,768];[196,768])\to [197,768]$$

代码实现为：

nn.cat([class]tokent, token) 

$$\begin{gathered} [196,768]⟶\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}(\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s},[\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{s}]\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}) \\ ⟶\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}([196,768],[1,768]) \\ ⟶[197,768] \end{gathered}$$

2.2.3 Position Embedding层

然后关于Position Embedding(就是之前Transformer中讲到的Positional Encoding)，这里的Position Embedding采用的是一个可训练的参数（具体为1D Pos. Emb.），是直接叠加在tokens上的（$\oplus$），所以shape要一样。

意思是说，前面的类别编码是一个trainable params，这里的位置编码也是一个trainable params，都是需要学习才能使得网络比较好的work。

以ViT-B/16为例，刚刚拼接[class]token（类别序列）后tokens的shape是 $[197,768]$ ，那么这里的Position Embedding的shape也是 $[197,768]$。

• 与《Transformer Is All You Need》不同，ViT作者没有使用固定的function去做Position Embedding，而是使用可训练的Position Embedding。
• 一般ViT都是可训练的Position Embedding

2.2.3.1 Position Embedding有效性说明

对于Position Embedding作者也有做一系列对比试验，在源码中默认使用的是1D Pos. Emb.，对比不使用Position Embedding准确率提升了大概3个点，和2D Pos. Emb.比起来没太大差别。

• No Pos. Emb.: 不使用位置编码
• 1-D Pos. Emb.: 使用一维位置编码
• 2-D Pos. Emb.: 使用二维位置编码
• Rel Pos. Emb.: 使用相对位置编码

• “The differences in how to encode spatial information is less important”
• 位置编码很重要，但如何进行位置编码不是那么重要

论文展示了训练得到的位置编码的每个位置与其他位置的余弦相似度的热力图。这里的Patch Size为 $32\times 32$ ，即一张图片可以被划分为 $224/32\times 224/32=7\times 7$ 个patch，每个patch的shape为：$[32,32,3]$，共 $7\times 7=49$ 个，我们可以对每个patch进行线性映射得到所需要的token $[32\times 32\times 3]=[3072]$，即

$$\underset{\mathrm{I}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{s}}{[224,224,3]}\to \underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{n}\mathrm{u}\mathrm{m}}{49}\times \underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}{[32,32,3]}\to \underset{\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{n}\mathrm{u}\mathrm{m}}{49}\times \underset{\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}}{[3072]}$$

即一张图片被切分为49个patch，对每个patch进行变换后得到shape为 $[3072]$ 的token，即tokens的shape为 $[49,3072]$。

Patch Size为 $32\times 32$ 表示：一个patch代表输入图片中多大的区域，所以Patch Size就是patch的shape，而patch个数如下所示。
$$\begin{gathered} \mathrm{P}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}.\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}=[\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e}[0],\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e}[1],\mathrm{C}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{l}] \\ \mathrm{p}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{n}\mathrm{u}\mathrm{m}=\frac{\mathrm{I}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e}}{\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e}[0]}\times \frac{\mathrm{I}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e}}{\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e}[1]} \end{gathered}$$

上图中，7×7的热力图表示一共有49个patch，其中每一个小图代表一个patch？？？？？？？
注意，这里并不是每一个小图代表一个patch，而是每一个小图是一个patch和其余48个patch的余弦相似度热力图，我们可以观察，里面的小图也是7×7的，而patch一共有7×7个，所以这样的理解是正确的。

Position Embedding会对每一个patch(patches)都叠加（$\oplus$）一个位置编码（其实应该是对每一个token(tokens)都叠加了位置编码，而tokens就是patches展平后的结果，所以这样说这是可以的）。针对每一个patch的位置编码与其他patch的位置编码求解余弦相似度，就可以得到上图了。

红色框框起来的是第一个patch与其余48个patch的余弦相似度热力图。它的第一行第一列的就是第一个patch与自己的余弦相似度热力图，自己与自己肯定是最相似的，所以值为1。而且它与其所在的行和列的相似度都挺高的，我们观察其他的patch也是如此，均和自己所在行列的相似度高一些。

这张热力图说明通过训练的确学习到了位置编码。

2.3 Transformer Encoder详解

Transformer Encoder其实就是重复堆叠Encoder Block $L$ 次，下图是霹雳吧啦Wz绘制的Encoder Block，主要由以下几部分组成：

• Layer Norm，这种Normalization方法主要是针对NLP领域提出的，这里是对每个token进行Norm处理，之前霹雳吧啦Wz也有讲过Layer Norm，不懂的可以参考Layer Normalization解析
• Multi-Head Attention，这个结构之前霹雳吧啦Wz在讲Transformer中很详细的讲过，不再赘述，不了解的可以参考详解Transformer中Self-Attention以及Multi-Head Attention
• Dropout/ DropPath，在原论文的代码中是直接使用的Dropout层，在但rwightman实现的代码中使用的是DropPath（stochastic depth），可能后者会更好一点。
• MLP Block，如下图所示，就是全连接+GELU激活函数+Dropout组成也非常简单，需要注意的是第一个全连接层会把输入节点个数翻4倍： $[197,768]\to [197,3072]$，第二个全连接层会还原回原节点个数： $[197,3072]\to [197,768]$：

$$\begin{gathered} [197,768]\underset{\mathrm{F}{\mathrm{C}}_1}{\to }[197,3072]\underset{\mathrm{F}{\mathrm{C}}_2}{\to }[197,768] \\ \mathrm{F}{\mathrm{C}}_{\mathrm{i}}=\mathrm{D}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}(\mathrm{G}\mathrm{E}\mathrm{L}\mathrm{U}(\mathrm{L}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}(\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}{\mathrm{n}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}}))) \end{gathered}$$

2.4 MLP Head详解

上面通过Transformer Encoder后输出的shape和输入的shape是保持不变的，以ViT-B/16为例， $[197,768]\underset{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{r}}{\to }[197,768]$。

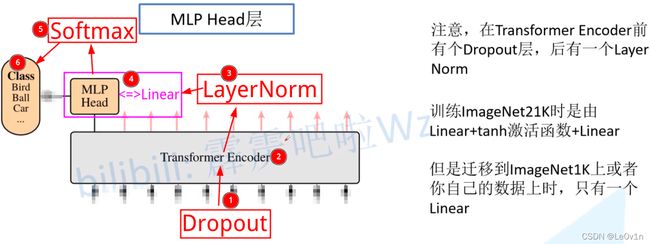
注意，在Transformer Encoder之前有一个Dropout层没有画出来，在Transformer Encoder之后有一个LayerNorm层没有画出来，后面有霹雳吧啦Wz画的ViT的模型可以看到详细结构。
这里我们只需要分类的信息，所以我们只需要提取出[class]token生成的对应结果就行，即 $[197,768]$ 中抽取出[class]token对应的一维向量（序列） $[1,768]$：

$$[197,768]\underset{\mathrm{M}\mathrm{L}\mathrm{P}\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{d}}{\to }[1,768]$$

• $[1,768]$ 就是图片被分为不同patch，每个patch的token
• $[197,768]$ 就是整个图片的token( $[196,768]$ )和分类token( $[1,768]$ )拼接在一起的结果

接着我们通过MLP Head得到我们最终的分类结果。

MLP Head原论文中说在训练ImageNet21K时是由Linear+Tanh激活函数+Linear组成。但是迁移到ImageNet1K上或者自己的数据上时，只用一个Linear即可：

• 从头训练: Linear + Tanh + Linear
• 迁移学习：Linear

简单理解，我们自己用，MLP Head等价于nn.Linear

在MLP Head得到结果后，如果我们想输入类别概率，接一个Softmax激活函数即可，真·流程图如下：

2.5 霹雳吧啦Wz绘制的Vision Transformer网络结构

为了方便大家理解，霹雳吧啦Wz根据源代码画了张更详细的图(以ViT-B/16为例)：

霹老师YYDS

1. 输入图片shape为 $[224,224,3]$
2. 通过Patch Embedding，即一个卷积 + Flatten()，生成shape为 $[196,768]$ 的tokens
3. 进行Class Embedding，即torch.concat(tokens, cls_token)
   cls_token为可训练参数，tokens的shape变化为：
   $$[196,768]\to [197,768]$$
4. Position Embedding，加上位置编码tokens，即tokens = tokens + pos_tokens
   pos_tokens为可训练参数，tokens的shape变化为：
   $$[197,768]\to [197,768]$$
5. 通过Dropout层
6. 经过 $L$ 层Transformer Encoder( 默认$L=12$ )
7. 经过LayerNorm层，shape为 $[197,768]$
8. 提取Class Token所对应的输出
   这里的实现为切片，对 $[197,768]$ 进行切片，只需要提取出Class Token对应的输出( $[1,768]$ )即可
9. 通过MLP Head得到最终的输出
   在自己训练集上使用，Pre-Logits就不要了，MLP Head就是nn.Linear
10. [可选]通过Softmax得到概率输出

2.6 Hybrid模型详解

在论文4.1章节的Model Variants中有比较详细的讲到Hybrid混合模型，就是将传统CNN特征提取和Transformer进行结合。下图绘制的是以ResNet50作为特征提取器的混合模型，但这里的ResNet与之前讲的ResNet有些不同。

1. R50的卷积层采用的是StdConv2d而非传统的Conv2d
2. 将所有的BatchNorm层（BN层）替换成GroupNorm层（GN）
3. 将Stage-4中的3个Block移至Stage-3中

• 在原ResNet-50网络中，Stage-1重复堆叠3次，Stage-2重复堆叠4次，Stage-3重复堆叠6次，Stage-4重复堆叠3次，但在这里的R50中，把Stage-4中的3个Block移至Stage-3中，所以Stage-3中共重复堆叠6+3=9次。
  为什么这么做
• 如果Stage-4存在的话，下采样率应为32，现在将Stage-4的Block移至Stage-3，那么下采样率为16。

1. 输入图片shape为 $[224,224,3]$
2. 先通过R50 Backbone进行特征提取，而不像ViT那样，直接使用nn.conv2d(in_channels=224, out_channels=768, kernel=(16, 16), stride=16)来实现。
   1. StdConv2d(inp, oup=64, kernel=(7,7), stride=2)
      $$[224,224,3]\to [112,112,64]$$
   2. GN, ReLU, MaxPool
      $$[112,112,64]\to [56,56,64]$$
3. Stage3 $\times 9$: $[56,56,64]\to [56,56,256]$
4. Stage2 $\times 4$: $[56,56,256]\to [28,28,512]$
5. Stage1 $\times 3$: $[28,28,512]\to [14,14,1024]$

Note: 这样刚好由[224, 224, 3]转换为[14, 14, 1024]，feature size正好是16倍，这和ViT中直接使用一个卷积的下采样率是一样的（都是16倍）

6. . Patch Embedding
   1. nn.Conv2d(inp, oup=768, kernel=(1, 1), stride=1)
      1. 因为前面的R50的采样率为16，feature size已经为14×14了，所以在Patch Embedding时就不需要进行下采样了，所以kernel=1, stride=1
      2. 1.2 调整通道数到768
   2. Flatten()得到tokens $[196,768]$
7. 后面的和ViT是一样的了

• 在纯Visual Transformer中，Patch Embedding的实现为：
  nn.conv2d(in_channels=224, out_channels=768, kernel=(16, 16), stride=16)
• 在Hybrid Transformer中，Patch Embedding的实现为：
  nn.conv2d(in_channels=1024, out_channels=1, kernel=(1, 1), stride=1)

3. 实验结果

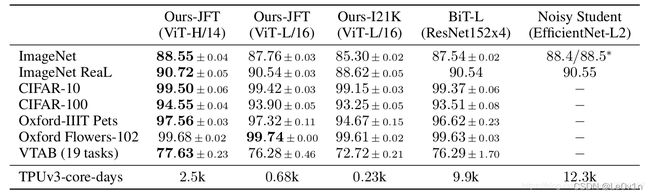
下表是论文用来对比ViT，ResNet（和刚刚讲的一样，使用的卷积层和Norm层都进行了修改）以及Hybrid模型的效果。通过对比发现：

• 在训练epoch较少时Hybrid优于ViT -> Epoch小选Hybrid
• 当epoch增大后ViT优于Hybrid -> Epoch大选ViT

4. ViT模型可调参数

在论文的Table 1中有给出三个模型（Base/ Large/ Huge）的参数，在源码中除了有Patch Size为 $16\times 16$ 的外还有 $32\times 32$ 的。

Model	Patch Size	Layers	Hidden Size D	MLP Size	Heads	Params
ViT-Base	16×16	12	768	3072	12	86M
ViT-Large	16×16	24	1024	4096	16	307M
ViT-Huge	14×14	32	1280	5120	16	-

其中：

• Layers就是Transformer Encoder中重复堆叠Encoder Block的次数 $L$
• Hidden Size就是对应通过Embedding层(Patch Embedding + Class Embedding + Position Embedding)后每个token的dim（序列向量的长度）
  不用那么复杂，其实就是Patch Embedding后向量的长度
• MLP Size是Transformer Encoder中MLP Block第一个全连接的节点个数（是token长度的4倍）
  • MLP中第一个全连接层升维数
  • 其实也是MLP的核心思想，先升维/降维，再提取特征，最后恢复维度
• Heads代表Transformer中Multi-Head Attention的heads数。

5. 与其他模型对比

Mode	File Size	Trainable Params (M)	Analysis
3D MobileNet v2	19.2 MB	589	-
3D MnasNet_v1	30.0 MB	244	-
3D ConvNeXt	114.6 MB	2325	too hard to train
3D ViT_patchsize_16	-	36782	too hard to train
3D ViT_patchsize_32	831.9 MB	10444	too hard to train
3D ViT_Hybrid	93.3 MB	2847	too hard to train

总结，没钱勿扰