Pandas 分析斐波那契数列模整数的周期问题
Pandas 分析斐波那契数列模整数的周期问题
- 引言
- 一、改进 Pisano 周期计算
- 二、计算 Pisano 周期的循环节
- 三、快速计算任意斐波那契数模 m m m 的余数
- 四、计算模 100 万以内的 Pisano 周期
- 五、Pandas 分析 Pisano 周期数据
-
- 5.1 分析 Pisano 周期
- 5.2 斐波那契幸运数字
- 5.3 满足特殊 Pisano 周期的整数模数
- 5.4 考虑 100 100 100 万以内的素数情形
- 5.5 模 100 100 100 万以内的素数的斐波那契幸运数字
- 5.6 满足特殊 Pisano 周期的素数模数
- 5.7 基于特殊 Pisano 周期的素性判定新方法
- 5.8 对往前文章提出问题的部分回答
引言
在上一篇文章中我们提到,斐波那契数列模整数的周期即是 Pisano 周期。
例如斐波那契数列 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 ⋯ 1,1,2,3,5,8,13,21,34,55,89⋯ 1,1,2,3,5,8,13,21,34,55,89⋯ 模 2 2 2 的结果为 1 , 1 , 0 , 1 , 1 , 0 , 1 , 1 , 0 , 1 , 1 ⋯ 1,1,0,1,1,0,1,1,0,1,1⋯ 1,1,0,1,1,0,1,1,0,1,1⋯ ,故模 2 2 2 的 Pisano 周期为 3 3 3 。我们不妨记斐波那契数列模 n n n 的Pisano 周期为 p ( n ) p(n) p(n) ,则 p ( 2 ) = 3 p(2)=3 p(2)=3 。
模 3 3 3 的一个循环为: 1 , 1 , 2 , 0 , 2 , 2 , 1 , 0 1,1,2,0,2,2,1,0 1,1,2,0,2,2,1,0 ,故 p ( 3 ) = 8 p(3)=8 p(3)=8 。
模 4 4 4 的一个循环为: 1 , 1 , 2 , 3 , 1 , 0 1,1,2,3,1,0 1,1,2,3,1,0 ,故 p ( 4 ) = 6 p(4)=6 p(4)=6 。
在作者 22 年 8 月的这篇文章中,我们探讨过如何计算 Pisano 周期的问题,得到了模 1 1 1 万以内的素数的所有周期。但该方法并不十分有效,对于更大的整数范围将无能为力。
本文我们将首先改进前期文章Python 探讨斐波拉契数列模素数的周期问题关于Pisano 周期的计算,并进一步通过 Pandas 数据分析,来回答该文最后的问题1和问题4。
一、改进 Pisano 周期计算
首先通过观察知道,Pisano 周期始终以 1 、 0 1、0 1、0 结束,而这正是我们可以计算模 n n n 的循环的开始。以模 2 2 2 为例,要求模 2 2 2 的一个循环,可以按照公式进行:
0 + 1 ≡ 1 ( m o d 2 ) 0+1 \equiv 1 \;(mod \; 2) 0+1≡1(mod2) 其中 0 0 0 是起始的前一个值, 1 1 1 是起始的当前值,用 0 + 1 0+1 0+1 模 2 2 2 得到模序列里的第一个值是 1 1 1 。并更新此时的前一个值为上一次的当前值 1 1 1 ,此时的当前值为上面算出来的值 1 1 1 。
下一步则继续按公式计算(也就是前一个值与当前值的和再模 2 2 2):
1 + 1 ≡ 0 ( m o d 2 ) 1+1 \equiv 0 \;(mod \; 2) 1+1≡0(mod2) 则得模序列里的第二个值 0 0 0 。再次更新此时的前一个值为上一次的当前值 1 1 1 ,此时的当前值为算出来的值 0 0 0 。
接下来我们有:
1 + 0 ≡ 1 ( m o d 2 ) 1+0 \equiv 1 \;(mod \; 2) 1+0≡1(mod2) 则得模序列里的第三个值 1 1 1 。并更新此时的前一个值为上一次的当前值 0 0 0 ,此时的当前值为算出来的值 1 1 1 。
由于此步的前一个值 0 0 0 和 当前值 1 1 1 与起始的前一个值和起始的当前值重合,说明我们刚刚经历了一次完整的模 2 2 2 的 Pisano 周期。由于进行了 3 3 3 次计算,因此模 2 2 2 的 Pisano 周期 p ( 2 ) = 3 p(2)=3 p(2)=3 。
结合上面的算法思想,我们写成下述 Python 代码来实现模任意整数 Pisano 周期的快速计算:
def pisanoPeriod(n):
previous, current = 0, 1
for i in range(0, n * n):
previous, current = current, (previous + current) % n
if (previous == 0 and current == 1):
return i + 1
这个方法摈弃了预先计算斐波那契数列的过程,计算速度明显更快。
在上述代码的循环中,循环次数的上限取值为 n 2 n^2 n2 是有理论依据的。我们先给出下述定理,出处见 Problems and Solutions: Solutions: E3410 。
定理1 \; 关于 Pisano 周期,我们有 p ( n ) ≤ 6 n p(n)\leq 6n p(n)≤6n ,等号成立当且仅当 n = 2 ⋅ 5 r n = 2 · 5^r n=2 ⋅ 5r ,其中 r ≥ 1 r\geq 1 r≥1 。如果 n n n 不是 2 ⋅ 5 r 2 · 5^r 2 ⋅ 5r 的形式,则 p ( n ) ≤ 4 n p(n)\leq 4n p(n)≤4n 。
定理1中的上界 6 n 6n 6n 在 n ≥ 6 n\geq 6 n≥6 时,是满足 6 n ≤ n 2 6n\leq n^2 6n≤n2 ,且易验证,当 n ≤ 5 n\leq 5 n≤5 时, p ( n ) < n 2 p(n)
二、计算 Pisano 周期的循环节
有了关于 Pisano 周期的计算,我们可以很方便地计算 Pisano 周期的循环节。Python 代码如下:
m = 5
p = pisanoPeriod(m)
for n in range(1, p+1):
print(fibonacciModulo(n, m))
通过计算,我们得到模 5 5 5 的 Pisano 周期的循环节为:
1 , 1 , 2 , 3 , 0 , 3 , 3 , 1 , 4 , 0 , 4 , 4 , 3 , 2 , 0 , 2 , 2 , 4 , 1 , 0 1,1,2,3,0,3,3,1,4,0,4,4,3,2,0,2,2,4,1,0 1,1,2,3,0,3,3,1,4,0,4,4,3,2,0,2,2,4,1,0 显然 p ( 5 ) = 20 p(5)=20 p(5)=20 。
三、快速计算任意斐波那契数模 m m m 的余数
假设我们计算 F 2023 F_{2023} F2023 模 5 5 5 ,实际上有如下性质可以简化计算:
F 2023 ≡ F 2023 ( m o d p ( 5 ) ) ≡ F 3 ≡ 2 ( m o d 5 ) F_{2023} \equiv F_{2023\;(mod \;p(5))}\equiv F_{3}\equiv 2 \; (mod \; 5) F2023≡F2023(modp(5))≡F3≡2(mod5) 一般地,我们有结论:
定理2 \; 斐波那契数 F n F_n Fn 模 m m m 的余数计算如下: F n ≡ F n m o d p ( m ) ( m o d m ) F_{n} \equiv F_{n\; mod \;p(m)} \; (mod \; m) Fn≡Fnmodp(m)(modm)
结合上面定理,我们可以类似地写出如下计算 F n F_n Fn 模 m m m 的 Python 代码:
def fibonacciModulo(n, m):
# 计算更小的下标 n
n = n % pisanoPeriod(m)
previous, current = 0, 1
if n==0:
return 0
elif n==1:
return 1
for i in range(n-1):
previous, current = current, previous + current
return (current % m)
fibonacciModulo(12345678901, 2023)
经计算可得 F 12345678901 ≡ 2007 ( m o d 2023 ) F_{12345678901} \equiv 2007 \;(mod \; 2023) F12345678901≡2007(mod2023) 。
四、计算模 100 万以内的 Pisano 周期
实际上我们可以直接给出下述代码:
# 产生模 100 万以内的 Pisano 周期
p = []
for i in range(2, 1000001):
p.append(pisanoPeriod(i))
with open("period.txt","w") as f:
f.write(str(p))
经过大约八九个小时的计算,我们可以得到最后的结果,并保存为一个 6.91 MB 的文件 period.txt 。模 100 万以内的 Pisano 周期的起始部分截图如下:
五、Pandas 分析 Pisano 周期数据
5.1 分析 Pisano 周期
我们先创建一个以模数为第一列,Pisano 周期为第二列的的 DataFrame:
import pandas as pd
a = [i for i in range(2, 1000001)]
c = {'Order' : a,
'Period' : p}
data = pd.DataFrame(c)
接着根据周期排序:
data.sort_values(by="Period", ascending=False)
得到如下结果:
可知模 100 万以内的整数,当模数 m = 781250 m=781250 m=781250 时,Pisano 周期最大,最大周期为 p ( 781250 ) = 4687500 p(781250)=4687500 p(781250)=4687500 。实际上, p ( 781250 ) = 6 × 781250 p(781250)=6\times 781250 p(781250)=6×781250 ,正好满足 6 6 6 倍关系,此时 781250 = 2 ⋅ 5 8 781250=2\cdot 5^8 781250=2⋅58 ,满足定理1。
468.75 468.75 468.75 万的周期,我们可能觉得太不可思议了。然而更有
lim sup n → ∞ p ( n ) = ∞ \limsup_{n\to \infty} \; p(n)=\infty n→∞limsupp(n)=∞ 接着可以按照周期排序:
data_ascending = data.sort_values(by="Period", ascending=True)
data_ascending.head(20)
将 Pisano 周期绘制成散点图:
import matplotlib.pyplot as plt
x = [i for i in range(1, 1000000)]
plt.figure(figsize=(10, 5), dpi=80)
plt.scatter(x, data_ascending['Period'], s=1)
plt.show()
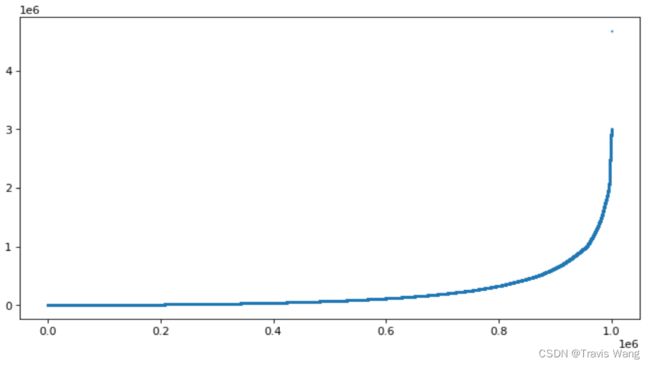 如上所示,我们将 Pisano 周期按由小到大的顺序排列(重复周期值不去重),以该序列的顺序号为横坐标,最后形成一条规律的曲线(最后一个离群值除外)。
如上所示,我们将 Pisano 周期按由小到大的顺序排列(重复周期值不去重),以该序列的顺序号为横坐标,最后形成一条规律的曲线(最后一个离群值除外)。
进一步表明,在按顺序排列的前 60 60 60 万个周期,Pisano 周期的值增长缓慢;而在后 40 40 40 万个周期,Pisano 周期值的增长越来越迅速,尤其在 100 100 100 万的附近。
实际上,Pisano 周期超过 100 100 100 万的数据相对较少,绝大部分的数据对应的 Pisano 周期都在 100 100 100 万以下。我们对 Pisano 周期大于 100 100 100 万的数据进行统计:
data_ascending[data_ascending['Period']>1000000].describe()
经过简单计算,发现 Pisano 周期大于 100 100 100 万的数据共有 44 , 204 44,204 44,204 个,仅占总体数据的 4.42 % 4.42\% 4.42% 。此部分数据 Pisano 周期的平均值为 1 , 502 , 636 1,502,636 1,502,636 ,中位数为 1 , 389 , 560 1,389,560 1,389,560。
反过来,Pisano 周期小于 100 100 100 万的数据共 955 , 795 955,795 955,795 个,占总体数据的 95.58 % 95.58\% 95.58% 。此绝大部分数据的 Pisano 周期的平均值仅为 156 , 511 156,511 156,511 ,中位数仅为 60 , 816 60,816 60,816。
现在我们改用将 ‘Order’ 字段作为横坐标,绘制 Order-Period 散点图如下:
plt.figure(figsize=(10, 5), dpi=80)
plt.scatter(data_ascending['Order'], data_ascending['Period'],
s=0.5, c='c')
plt.show()
x = [i for i in range(1, 1000000)]
plt.figure(figsize=(10, 5), dpi=80)
plt.scatter(data_ascending['Order'], data_ascending['Period'],
s=0.5, c='c')
plt.scatter(x, 3*np.array(x), s=0.5, c='m')
plt.scatter(x, 2*np.array(x), s=0.5, c='b')
plt.show()
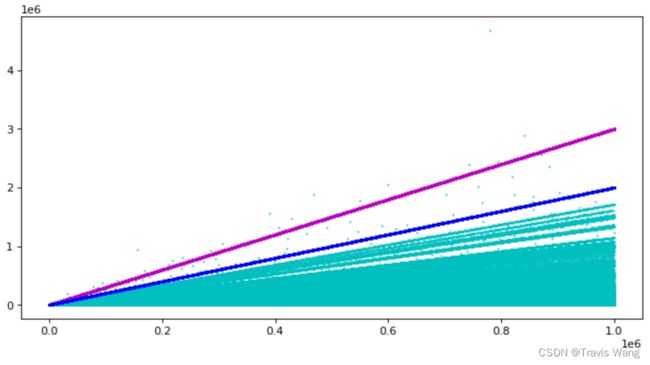
对比发现,上面的红线和蓝线几乎就与之前的两根绿线重合。也就是说, p ( n ) ≤ 3 n p(n)\leq 3n p(n)≤3n 对绝大多数数据都是成立的。而且 Pisano 周期取值满足 2 n < p ( n ) ≤ 3 n 2n
5.2 斐波那契幸运数字
现在我们来回答文章Python 探讨斐波拉契数列模素数的周期问题中的问题4。也就是回答“当范围扩大到模 1 , 000 , 000 1,000,000 1,000,000 以内的整数时,对应斐波那契数列的幸运数字是多少 ?” 因为比较容易,下面直接给出求解代码:
# 寻找 100 万以内的斐波那契幸运数字
data_ascending['Ratio'] = data_ascending['Order'] / data_ascending['Period']
data_ascending_ratio = data_ascending.sort_values(by="Ratio", ascending=False)
data_ascending_ratio.head(20)
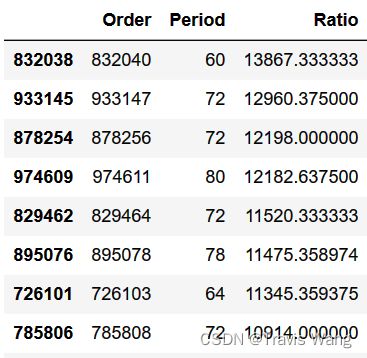
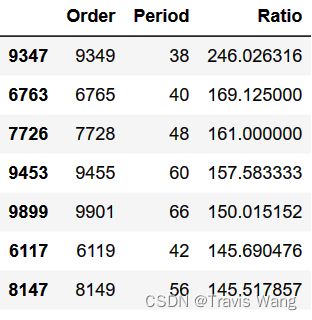
很显然,模 100 100 100 万以内的整数的斐波那契幸运数字是 832 , 040 832,040 832,040 ,其周期为 60 60 60 ,模数与周期的比率竟然达到了惊人的 13867.33 13867.33 13867.33 !而在之前我们讨论的模 1 1 1 万以内的素数的斐波那契幸运数字是 9349 9349 9349 ,其模数与周期的比率也才 246.03 246.03 246.03 。
反过来,我们也可以求模 100 100 100 万以内的整数的斐波那契霉运数字。代码如下:
data_ascending_ratio.tail(20)
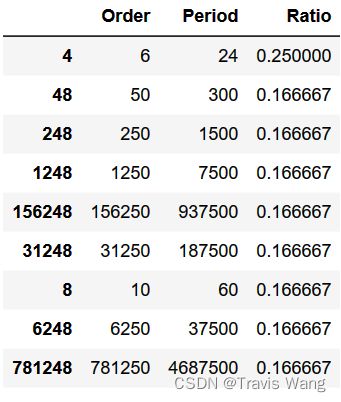
由上结果可知,模 100 100 100 万以内的整数的斐波那契霉运数字一共有 8 8 8 个:
10 、 50 、 250 、 1250 、 6250 、 31250 、 156250 、 781250 10、50、250、1250、6250、31250、156250、781250 10、50、250、1250、6250、31250、156250、781250 实际上,这些数字 n n n 都满足 p ( n ) = 6 n p(n)=6n p(n)=6n ,且构成公比为 5 5 5 的等差数列。越往后面,对应的 Pisano 周期会非常之大。
5.3 满足特殊 Pisano 周期的整数模数
接下来我们求斐波那契数列模整数 n n n 的周期为 2 n + 2 2n+2 2n+2 的 n n n 的个数。
period_2n2 = data[2*data['Order']+2 == data['Period']]
period_2n2.head(20)
通过语句 ‘period_2n2.shape’ 得到 30 , 917 30,917 30,917 个数 n n n 满足模 n n n 的周期为 2 n + 2 2n+2 2n+2 。
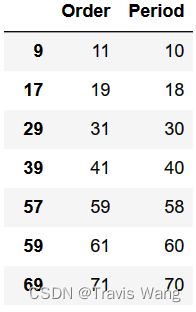
同理,我们求斐波那契数列模整数 n n n 的周期为 n − 1 n-1 n−1 的 n n n 的个数。
period_n1 = data[data['Order'] - 1 == data['Period']]
period_n1.head(20)
得到 20 , 911 20,911 20,911 个数 n n n 满足模 n n n 的周期为 n − 1 n-1 n−1 。
5.4 考虑 100 100 100 万以内的素数情形
现在我们会问,模 100 100 100 万以内的素数的斐波那契幸运数字。这时候,需要一张 100 100 100 万以内的素数表:
先导入该表:
prime = pd.read_csv(r"C:\Users\bigdata\Desktop\100万以内的素数.txt",
sep=',', header=None).T
prime
再来重新构建模 100 100 100 万以内的素数的 Pisano 周期表如下:
data_prime_order = pd.DataFrame()
for i in prime[0]:
data_prime_order = data_prime_order.append(data[data['Order']==i],
ignore_index=True)
data_prime_order.head(20)
求得 100 100 100 万以内全体 78 , 498 78,498 78,498 个素数的周期。
5.5 模 100 100 100 万以内的素数的斐波那契幸运数字
现在可以给出模 100 100 100 万以内的素数的斐波那契幸运数字的计算:
data_prime_order['Ratio'] = data_prime_order['Order'] / data_prime_order['Period']
data_prime_order_ascending_ratio = data_prime_order.sort_values(by="Ratio", ascending=False)
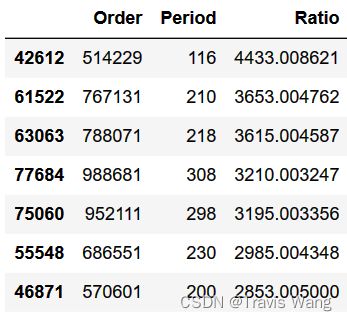
data_prime_order_ascending_ratio.head(20)
可以知道,模 100 100 100 万以内的素数的斐波那契幸运数字是 514 , 229 514,229 514,229 其比率达到了 4433 4433 4433 ,但远不如 832 , 040 832,040 832,040 的比率 13 , 867 13,867 13,867 来得大。
5.6 满足特殊 Pisano 周期的素数模数
接下来我们求斐波那契数列模素数 p p p 的周期为 2 p + 2 2p+2 2p+2 的 p p p 的个数。
period_2n2_prime = data_prime_order[2*data_prime_order['Order']+2 ==
data_prime_order['Period']]
period_2n2_prime.head(20)
通过 ‘.shape’ 命令同样可以求得一共有 30 , 917 30,917 30,917 个数 p p p 满足模 p p p 的周期为 2 p + 2 2p+2 2p+2 。这与之前求得的模整数 n n n 的情形得到的个数 30 , 917 30,917 30,917 一致!
同理可求斐波那契数列模素数 p p p 的周期为 p − 1 p-1 p−1 的 p p p 的个数。
period_n1_prime = data_prime_order[data_prime_order['Order'] - 1
== data_prime_order['Period']]
period_n1_prime.head(20)
得到 20 , 911 20,911 20,911 个数 p p p 满足模 p p p 的周期为 p − 1 p-1 p−1 ,这又与之前求得的模整数 n n n 的情形得到的个数 20 , 911 20,911 20,911 一致!
进一步通过如下代码可以判断斐波那契数列模整数 n n n 的周期为 2 n + 2 2n+2 2n+2 的全体 n n n 与斐波那契数列模素数 p p p 的周期为 2 p + 2 2p+2 2p+2 的所有 p p p 的是否完全一致:
(period_n1_prime['Order'].values == period_n1['Order'].values).all()
结果返回的是 True ,说明 100 100 100 万以内,满足斐波那契数列模整数 n n n 的周期为 n − 1 n-1 n−1 的全体 n n n 皆为素数。
同样验证另一部分:
(period_2n2_prime['Order'].values == period_2n2['Order'].values).all()
结果返回的也是 True ,说明 100 100 100 万以内,满足斐波那契数列模整数 n n n 的周期为 2 n + 2 2n+2 2n+2 的全体 n n n 皆为素数。
我们引用一下文章Python 探讨斐波拉契数列模素数的周期问题中的定理:
定理3 设 { F n } \{F_n\} {Fn} 为斐波那契数列, p p p 为大于 5 5 5 的素数,数列 F \mathscr{F} F 为斐波那契数列 { F n } \{ F_n \} {Fn} 模素数 p p p 后的新数列,则当 p = 1 , 4 m o d 5 p = 1, 4 \mod 5 p=1,4mod5 时, F \mathscr{F} F 的周期为 p − 1 p-1 p−1 或 p − 1 p-1 p−1 的因子;当 p = 2 , 3 m o d 5 p = 2, 3 \mod 5 p=2,3mod5 时, F \mathscr{F} F 的周期为 2 p + 2 2p+2 2p+2 或 2 p + 2 2p+2 2p+2 的因子。
由上述定理,我们知道,还有一部分素数 p p p ,使得斐波那契数列 { F n } \{ F_n \} {Fn} 模素数 p p p 的 Pisano 周期是 p − 1 p-1 p−1 或 2 p + 2 2p+2 2p+2 的真因子。因此我们可以讨论模素数与模整数的情形是否也有两者一致的结果。
我们先讨论斐波那契数列 { F n } \{ F_n \} {Fn} 模整数 n n n 的周期是 n − 1 n-1 n−1 的真因子的情形:
period_mod_n1 = data[((data['Order']-1)%data['Period']==0) &
(data['Period']!=data['Order']-1)]
period_mod_n1
结果显示有 18352 18352 18352 个 n n n 满足该情形。
然后讨论斐波那契数列 { F n } \{ F_n \} {Fn} 模素数 p p p 的周期是 p − 1 p-1 p−1 的真因子的情形:
period_mod_n1_prime = data_prime_order[((data_prime_order['Order']-1)%data_prime_order['Period']==0) &
(data_prime_order['Period']!=data_prime_order['Order']-1)]
period_mod_n1_prime
结果显示有 18299 18299 18299 个 p p p 满足该情形。对比模 n n n ,发现两者不同,模 n n n 时多包含了 53 53 53 个合数模。例如 n = 999941 = 577 × 1733 n=999941=577\times 1733 n=999941=577×1733 , p ( 999941 ) = 1156 p(999941)=1156 p(999941)=1156 ,仍然满足关系式 p ( n ) ∣ n − 1 p(n)\;| \;n-1 p(n)∣n−1 。不满足为素数的情形仅占 53 / 18352 ≈ 0.29 % 53/18352\approx 0.29\% 53/18352≈0.29% 。
另一面考虑斐波那契数列 { F n } \{ F_n \} {Fn} 模整数 n n n 的周期是 2 n + 2 2n+2 2n+2 的真因子的情形:
period_mod_2n2 = data[((2*data['Order']+2)%data['Period']==0) &
(data['Period']!=2*data['Order']+2)]
period_mod_2n2
结果显示有 8498 8498 8498 个 n n n 满足该情形。
最后讨论斐波那契数列 { F n } \{ F_n \} {Fn} 模素数 p p p 的周期是 2 p + 2 2p+2 2p+2 的真因子的情形:
period_mod_2n2_prime = data_prime_order[((2*data_prime_order['Order']+2)%data_prime_order['Period']==0) &
(data_prime_order['Period']!=2*data_prime_order['Order']+2)]
period_mod_2n2_prime
结果显示有 8370 8370 8370 个 p p p 满足该情形。对比模 n n n ,发现两者不同,模 n n n 时多包含了 128 128 128 个合数模。例如 n = 44 = 2 2 × 11 n=44=2^2\times 11 n=44=22×11 , p ( 44 ) = 30 p(44)=30 p(44)=30 ,仍然满足关系式 p ( n ) ∣ 2 n + 2 p(n)\;| \;2n+2 p(n)∣2n+2 。不满足为素数的情形仅占 128 / 8498 ≈ 1.5 % 128/8498\approx 1.5\% 128/8498≈1.5% 。
综上所述,依据定理3我们可以在此提出一个新猜测:
猜测1 \; 满足斐波那契数列模整数 n n n 的周期为 n − 1 n-1 n−1 的全体 n n n 皆为素数;满足斐波那契数列模整数 n n n 的周期为 2 n + 2 2n+2 2n+2 的全体 n n n 皆为素数;仅有少数的整数 n n n ,虽然满足斐波那契数列模 n n n 的周期为 n − 1 n-1 n−1 或 2 n + 2 2n+2 2n+2 的真因子,但它们是合数(绝大部分是素数)。
其中唯独素数 5 5 5 比较特殊,其不满足猜测1,是因为定理3是排除了 5 5 5 了的。 5 5 5 的 Pisano周期不属于上述任何一个情形,而小于 5 5 5 的素数 2 2 2、 3 3 3 却是符合上述猜测的。
5.7 基于特殊 Pisano 周期的素性判定新方法
基于上述猜测1,我们可以给出整数 n n n 的素性判定的新方法:
n = 23456789
if pisanoPeriod(n) == 2*n+2:
print(f'{n} 是素数')
elif pisanoPeriod(n) == n-1:
print(f'{n} 是素数')
elif ((2*n+2)%pisanoPeriod(n)==0) or ((n-1)%pisanoPeriod(n)==0):
print(f'{n} 是概率素数')
else:
print(f'{n} 是合数')
得到的结果是: 23456789 23456789 23456789 是概率素数,依概率来看, 23456789 23456789 23456789 大概率是素数。我们再次经过 GP 语言验证,确定了 23456789 23456789 23456789 是素数。
如果数字超过 1 1 1 亿,计算的复杂度就会增加,因为此时 Pisano 周期的计算会比较慢。比如 1234567891 1234567891 1234567891 的计算就要花几分钟。得到结果仍然为: 1234567891 1234567891 1234567891 是概率素数。再运用 GP 语言验证,同样确定了 1234567891 1234567891 1234567891 是素数。
当 n n n 取 100 , 000 , 007 100,000,007 100,000,007 时,程序运行得到的结果为: 100000007 100000007 100000007 是素数。进一步验证该数也的确为素数。
结合定理3可知,除了 5 5 5 以外,该方法判定出一个合数的结论是 100 % 100\% 100% 正确的,但也有小概率会得到一个合数是概率素数的情形,比如前面的 999941 999941 999941 ,被本程序判定为概率素数,但实际上它是一个合数。另一方面,基于前面的讨论,本程序在 100 100 100 万以内判定是素数的结论也是 100 % 100\% 100% 正确的。
5.8 对往前文章提出问题的部分回答
现在我们来回答文章Python 探讨斐波拉契数列模素数的周期问题中的问题1。
将范围扩大到模 1 , 000 , 000 1,000,000 1,000,000 以内的素数,则一共有 30 , 917 30,917 30,917 个模数 p p p 满足周期等于 2 p + 2 2p+2 2p+2 。有 20 , 911 20,911 20,911 个模数 p p p 满足周期等于 p − 1 p-1 p−1 。此时满足周期等于 2 p + 2 2p+2 2p+2 或 p − 1 p-1 p−1 的占比为 ( 30917 + 26670 ) / 78498 ≈ 0.733611 (30917+26670)/78498 \approx 0.733611 (30917+26670)/78498≈0.733611 。
最后,我们讨论 1 1 1 万以内、 10 10 10 万以内的幸运数字等情形,即回答问题4。
当模数小于 1 1 1 万时:
data_less10000 = data[data['Order'] < 10000]
data_less10000.tail(10)
计算比率如下:
data_less10000['Ratio'] = data_less10000['Order'] / data_less10000['Period']
data_less_ascending_ratio = data_less10000.sort_values(by="Ratio", ascending=False)
data_less_ascending_ratio.head(20)
这表明,模 1 1 1 万以内 整数的斐波那契幸运数字仍然是 9349 9349 9349 ,也就是说与模 1 1 1 万以内素数的斐波那契幸运数字是一致的!
通过与前面类似的计算,我们可以得到 1 1 1 万以内一共有 487 487 487 个模数 p p p 满足周期为 2 p + 2 2p+2 2p+2 ,一共有 322 322 322 个模数 p p p 满足周期为 p − 1 p-1 p−1 。满足周期等于 2 p + 2 2p+2 2p+2 或 p − 1 p-1 p−1 的占比为 0.6582587469487388 0.6582587469487388 0.6582587469487388 。
进一步我们可以得到, 10 10 10 万以内一共有 3803 3803 3803 个模数 p p p 满足周期为 2 p + 2 2p+2 2p+2 ,一共有 2553 2553 2553 个模数 p p p 满足周期为 p − 1 p-1 p−1 。并且满足周期等于 2 p + 2 2p+2 2p+2 或 p − 1 p-1 p−1 的素数占比为 0.6626355296080066 0.6626355296080066 0.6626355296080066 。
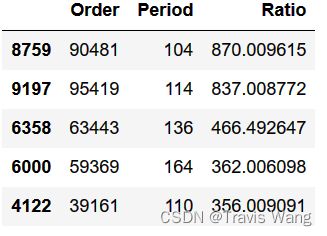
10 10 10 万以内模整数的幸运数字是 64079 64079 64079 ,比率是 1393 1393 1393 ; 10 10 10 万以内模素数的幸运数字是 90481 90481 90481 ,比率是 870 870 870 。
我们发现,随着素数 p p p 的取值范围的增加,满足 Pisano 周期等于 2 p + 2 2p+2 2p+2 或 p − 1 p-1 p−1 的占比由 0.658 0.658 0.658 、 0.663 0.663 0.663 直到 0.734 0.734 0.734 呈逐渐递增的趋势,预示着此占比似乎应该有个极限。
至于还有没有跟 9349 9349 9349 一样特殊的幸运数字(既是模整数又是模素数的幸运数字),这也是后续需要进一步验证的。