【图像配准】点云配准ICP算法介绍:基础流程、ICP算法的变种
ICP算法(Iterative Closest Points)
前言
ICP的目的:把不同坐标系中的点,通过最小化配准误差,变换到一个共同的坐标系中
配准:把匹配图像 配准到 参考图像的坐标系中
点云包括几何信息和非几何信息
点云数量非常巨大,并且含有噪声,所以需要滤波。滤波就是从带有噪声中提取有用的信息。
1)去除不能为匹配带来有用信息的点
2)点云进一步抽象,例如提取局部的法线信息或曲率
配准包括:粗配准、精配准
粗配准:大概配准,获得R和T的初值
精配准:不断迭代,计算最终的R和T。基本上使用ICP算法及其各种变种
拓展:
映射变换(三维)
H = [ r 11 r 12 r 13 t x r 21 r 22 r 23 t y r 31 r 32 r 33 t z v x v y v z s ] = [ R t V S ] H = \left[ \begin{array}{cccc} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ v_x & v_y & v_z & s \end{array} \right] = \left[ \begin{array}{cccc} R & t \\ V & S \end{array} \right] H=⎣⎢⎢⎡r11r21r31vxr12r22r32vyr13r23r33vztxtytzs⎦⎥⎥⎤=[RVtS]
R旋转矩阵、t平移向量、V透视变换向量、S比例因子
刚性变换矩阵中涉及到六个未知数α、β、γ、 tx、ty、tz。
要唯一确定这六个未知参数,需要六个线性方程,即至少需要在待匹配点云重叠区域找到3组对应点对,且3组对应点对不能共线,才可以得到这几个未知数的值,进而完成刚性矩阵的参数估计。
通常情况下,人们会选择尽可能多的对应点对,进一步提高刚性变换矩阵的参数估计精度。
问题引入
通过RGBD相机获取两组点云,在待匹配的两组点云数据的重叠区域内,选取两组点云,一组点云 P s P_s Ps(源),相机经过位姿变换(旋转平移)之后拍摄第二组点云 P t P_t Pt(平移后)。
理论上,两者内部的点应该是一一对应的,比如(Ps0,Pt0)对应同一个点。
并且在存储的时候,按照顺序存储下标为i的像素。
在没有误差的情况下,计算出旋转R和平移t,可以将 P s P_s Ps转换到 P t P_t Pt,转换公式为:
p t i = R ⋅ p s i + t p_t^i = R·p_s^i+t pti=R⋅psi+t
但由于噪声存在,以及匹配错误存在,上面的公式不一定对于所有的点都成立,所以存在误差。
ICP具体算法
1)核心:最小化一个目标函数,即上面提到的误差
f ( R , t ) = 1 N p ∑ i = 1 N p ∣ p t i − R ⋅ p s i − t ∣ 2 f(R,t)=\frac{1}{N_p}\sum_{i=1}^{N_p}|p_t^i-R·p_s^i-t|^2 f(R,t)=Np1i=1∑Np∣pti−R⋅psi−t∣2
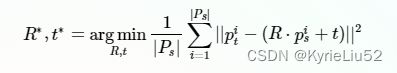
pt和ps为对应点,一共有Np对对应点,目标函数实际是对应点之间的欧氏距离求和
2)寻找对应点: 我们现在并不知道有哪些对应点。因此,我们在有初值的情况下,假设用初始的旋转平移矩阵对source cloud进行变换,得到的一个变换后的点云。然后将这个变换后的点云与target cloud进行比较,只要两个点云中存在距离小于一定阈值,我们就认为这两个点就是对应点。称为最邻近点对
3)R、T优化: 有了对应点之后,我们就可以用对应点对旋转R与平移T进行估计。这里R和T中只有6个自由度,而我们的对应点数量是庞大的(存在多余观测值)。因此,我们可以采用最小二乘等方法求解最优的旋转平移矩阵
4)迭代: 我们优化得到了一个新的R与T,导致了一些点转换后的位置发生变化,一些最邻近点对也相应的发生了变化。因此,我们又回到了步骤2)中的寻找最邻近点方法。2)3)步骤不停迭代进行,直到满足一些迭代终止条件,如R、T的变化量小于一定值,或者上述目标函数的变化小于一定值,或者邻近点对不再变化等。
算法大致流程就是上面这样。
ICP流程
1.预处理:滤波、清洗数据
2.匹配:利用粗配准的估计矩阵,找最邻近点
3.加权:调整一些对应点对的权重
4.剔除不合理的对应点对
5.计算Loss
6.最小化Loss,求解当前最优变换
7.重复执行2-6,迭代直到收敛
这里的优化过程是一个贪心的策略。
首先固定R跟T利用最邻近算法找到最优的点对,然后固定最优的点对来优化R和T,依次反复迭代进行。
ICP算法的参数主要有两个:一个是ICP的邻近距离,另外一个是迭代的终止条件。
邻近距离:最初使用较大的对应点距离参数,然后逐步减小到一个较小的值
整体上看,ICP也把配准分成两个子问题:找最邻近点、找最优变换
找最邻近对应点(Find Closet Point)
利用初始 R 0 、 t 0 R_0、t_0 R0、t0 或上一次迭代得到的 R k − 1 , t k − 1 R_{k-1},t_{k-1} Rk−1,tk−1, 对初始(源)点云进行变换,得到一个临时的变换点云,然后用这个点云和目标点云进行比较,找出源点云中每一个点在目标点云中的最近邻点。
如果直接进行比较找最近邻点,需要进行两重循环,计算复杂度为 O ( ∣ P s ∣ ⋅ ∣ P t ∣ ) O(|P_s|⋅|P_t|) O(∣Ps∣⋅∣Pt∣),这一步会比较耗时,常见的加速方法有:
- 设置距离阈值,当点与点距离小于一定阈值就认为找到了对应点,不用遍历完整个点集;
- 在目标点云中取点集 p t i 属 于 P t p_t^i属于P_t pti属于Pt,找出源点云中的对应点集 p s i 属 于 P s p_s^i属于P_s psi属于Ps,使得 ∣ ∣ p s i − p t i ∣ ∣ < = m i n ||p_s^i-p_t^i||<=min ∣∣psi−pti∣∣<=min
- 注意,此处的ps为源点云变换后的临时变换点云
- 使用 ANN(Approximate Nearest Neighbor) 加速查找,常用的有 KD-tree;KD-tree 建树的计算复杂度为
O(N log(N)),查找通常复杂度为O(log(N))(最坏情况下O(N))。
KD-Tree
一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构,主要应用于多维空间关键数据的搜索
k-d树是每个节点都为k维点的二叉树
所有的非叶子节点,都可以看做是一个超平面,把空间分割为两个半空间,左子树为超平面左边的点,右子树为超平面右边的点。
BSPTree(Binary space partitioning tree,空间二分树)
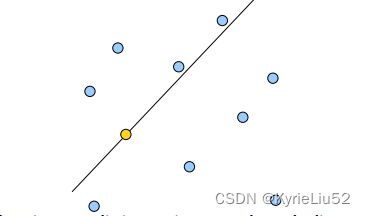
黄色的点作为根节点,上面的点归左子树,下面的点归右子树,接下来再不断地划分,最后得到一棵树就是赫赫有名的BSPTree(binary space partitioning tree)。
KDTree就是超平面都垂直于轴的BSPTree
上面的数据集用KDTree划分后为:

黄色节点就是Root节点,下一层是红色,再下一层是绿色,再下一层是蓝色。
创建kd树
kd树的数据结构
Node-data - 数据矢量, 数据集中某个数据点,是n维矢量(这里也就是k维)
Range - 空间矢量, 该节点所代表的空间范围
split - 整数, 垂直于分割超平面的方向轴序号
Left - k-d树, 由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
Right - k-d树, 由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
parent - k-d树, 父节点
建立树最大的问题在于轴点(pivot)的选择,选择好轴点之后,树的建立就和BSTree差不多了。
建树必须遵循两个准则:
1.建立的树应当尽量平衡,树越平衡代表着分割得越平均,搜索的时间也就是越少。
2.最大化邻域搜索的剪枝机会。
轴点选取策略:(从垂直哪个轴的超平面切割、切割点在哪)
1.median of the most spread dimension pivoting strategy
对于所有描述子数据(特征矢量),统计他们在每个维度上的数据方差,挑选出方差中最大值,对应的维就是split域的值。数据方差大说明沿该坐标轴方向上数据点分散的比较开。这个方向上,进行数据分割可以获得最好的平衡。数据点集Data-Set按照第split维的值排序,位于正中间的那个数据点 被选为轴点。
这种方法容易形成:
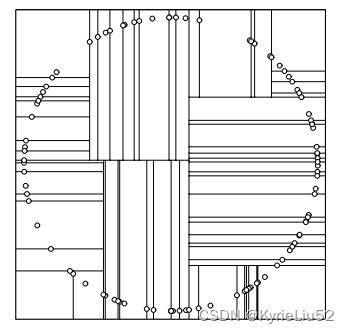
2.纬度的选择的依据为数据范围最大的那一维作为分割纬度,之后也是选中这个纬度的中间节点作为轴点,然后进行分割,结果:

这样的策略对最近邻搜索会比较友好。
3.随着树的深度,轮流选择轴作为分割面(例如:在三维空间中根节点是 x 轴垂直分割面,其子节点皆为 y 轴垂直分割面,其孙节点皆为 z 轴垂直分割面,其曾孙节点则皆为 x 轴垂直分割面,依此类推。)也是选中某纬度的中间节点作为轴点
选择中间节点进行划分,会产生一个平衡的kd树,但是平衡的树不一定对每个应用都是最佳的
最近邻搜索
找出在树中与输入点最接近的点
过程:
-
从根节点开始,递归的往下移。往左还是往右的决定方法与插入元素的方法一样(如果输入点在分区面的左边则进入左子节点,在右边则进入右子节点)。
-
一旦移动到叶节点,将该节点当作"当前最佳点"。
-
回溯搜索路径,并判断搜索路径上节点的其他子结点中是否可能有距离更近的点,如果有可能,就要对另一个子结点进行最近邻搜索
-
如何判断?
-
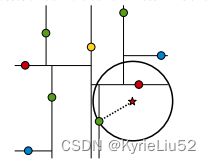
以查询点为圆心,以当前的最近距离为半径画圆,这个圆称为候选超球(candidate hypersphere),如果圆与回溯点的轴相交(也就是star点到红点切割轴的距离,小于star点和当前最佳点的距离),则认为其他子结点中可能有更近的点
-
个人对相交的理解:与当前最佳点的距离,比距离划分轴的距离还要远,说明轴的另一边有可能存在更近的点。
-
例子(不可能和可能两种情况):
- 当搜索路径为空时(向下搜索时,路过节点加入搜索路径;向上回溯时,路过节点从搜索路径中剔除),完成最邻近搜索。
求解最优变换(Find Best Transform)
对于 point-to-point ICP 问题,求最优变换是有闭形式解(closed-form solution)的,可以借助 SVD 分解来计算。
给出结论,在已知点的对应关系的情况下,
设 p ‾ s \overline p_s ps, p ‾ t \overline p_t pt 分别表示源点云和目标点云的质心
令 p ^ s i = p s i − p ‾ s \hat p_s^i = p_s^i-\overline p_s p^si=psi−ps, p ^ t i = p t i − p ‾ t \hat p_t^i = p_t^i-\overline p_t p^ti=pti−pt
令 H = ∑ i = 1 ∣ P s ∣ p ^ s i p ^ t i T H=\sum_{i=1}^{|P_s|}\hat p_s^i{\hat p_t^i}^T H=∑i=1∣Ps∣p^sip^tiT,这是一个 3x3 矩阵,对 H 进行 SVD 分解得到 H = U ∑ V T H=U\sum V^T H=U∑VT,则 point-to-point ICP 问题最优旋转为:
R ∗ = V U T R^*=VU^T R∗=VUT
最优平移为:
t ∗ = p ‾ t − R ∗ p ‾ s t^* = \overline p_t -R^*\overline p_s t∗=pt−R∗ps
下面分别给出证明。
计算最优平移
令 N = ∣ P s ∣ N = |P_s| N=∣Ps∣,设损失函数为 F ( t ) = ∑ i = 1 N ∣ ∣ ( R ⋅ p s i + t ) − p t i ∣ ∣ 2 F(t) = \sum_{i=1}^{N} ||(R \cdot p_s^i + t) - p_t^i||^2 F(t)=∑i=1N∣∣(R⋅psi+t)−pti∣∣2,求导可得
∂ F ∂ t = ∑ i = 1 N 2 ( R ⋅ p s i + t − p t i ) = 2 n t + 2 R ∑ i = 1 N p s i − 2 ∑ i = 1 N p t i \frac{\partial F}{\partial t} = \sum_{i=1}^{N} 2 (R \cdot p_s^i + t - p_t^i) \\ = 2nt + 2R\sum_{i=1}^{N}p_s^i - 2\sum_{i=1}^{N}p_t^i ∂t∂F=i=1∑N2(R⋅psi+t−pti)=2nt+2Ri=1∑Npsi−2i=1∑Npti
当导数为0时,最优,损失最小
t = 1 N ∑ i = 1 N p t i − R 1 N ∑ i = 1 N p s i = p ˉ t − R p ˉ s t = \frac{1}{N} \sum_{i=1}^{N} p_t^i - R \frac{1}{N} \sum_{i=1}^{N} p_s^i \\ = \bar p_t - R \bar p_s t=N1i=1∑Npti−RN1i=1∑Npsi=pˉt−Rpˉs
计算最优旋转
经过最优平移的推导,我们知道无论旋转如何取值,都可以通过计算点云的质心来得到最优平移
因此,为了计算方便,不考虑平移的影响,将源点云和目标点云都转换到质心坐标下,这就是之前为什么让 p ^ s i = p s i − p ‾ s \hat p_s^i = p_s^i-\overline p_s p^si=psi−ps, p ^ t i = p t i − p ‾ t \hat p_t^i = p_t^i-\overline p_t p^ti=pti−pt。
转化之后,我们不考虑平移,损失函数为:
F ( R ) = ∑ i = 1 N ∣ ∣ R ⋅ p ^ s i − p ^ t i ∣ ∣ 2 F(R) = \sum_{i=1}^{N} ||R \cdot \hat p_s^i - \hat p_t^i||^2 F(R)=i=1∑N∣∣R⋅p^si−p^ti∣∣2
化简 ∣ ∣ R ⋅ p ^ s i − p ^ t i ∣ ∣ 2 ||R \cdot \hat p_s^i - \hat p_t^i||^2 ∣∣R⋅p^si−p^ti∣∣2:
∣ ∣ R ⋅ p ^ s i − p ^ t i ∣ ∣ 2 = ( R ⋅ p ^ s i − p ^ t i ) T ( R ⋅ p ^ s i − p ^ t i ) = ( p ^ s i T R T − p ^ t i T ) ( R ⋅ p ^ s i − p ^ t i ) = p ^ s i T R T R p ^ s i − p ^ t i T R p ^ s i − p ^ s i T R T p ^ t i + p ^ t i T p ^ t i = ∣ ∣ p ^ s i ∣ ∣ 2 + ∣ ∣ p ^ t i ∣ ∣ 2 − p ^ t i T R p ^ s i − p ^ s i T R T p ^ t i = ∣ ∣ p ^ s i ∣ ∣ 2 + ∣ ∣ p ^ t i ∣ ∣ 2 − 2 p ^ t i T R p ^ s i ||R \cdot \hat p_s^i - \hat p_t^i||^2 = (R \cdot \hat p_s^i - \hat p_t^i)^T(R \cdot \hat p_s^i - \hat p_t^i) \\ = ({\hat p_s^i}^T R^T - {\hat p_t^i}^T)(R \cdot \hat p_s^i - \hat p_t^i) \\ = {\hat p_s^i}^T R^T R {\hat p_s^i} - {\hat p_t^i}^T R {\hat p_s^i} - {\hat p_s^i}^T R^T {\hat p_t^i} + {\hat p_t^i}^T {\hat p_t^i} \\ = ||{\hat p_s^i}||^2 + ||{\hat p_t^i}||^2 - {\hat p_t^i}^T R {\hat p_s^i} - {\hat p_s^i}^T R^T {\hat p_t^i} \\ = ||{\hat p_s^i}||^2 + ||{\hat p_t^i}||^2 - 2{\hat p_t^i}^T R {\hat p_s^i} ∣∣R⋅p^si−p^ti∣∣2=(R⋅p^si−p^ti)T(R⋅p^si−p^ti)=(p^siTRT−p^tiT)(R⋅p^si−p^ti)=p^siTRTRp^si−p^tiTRp^si−p^siTRTp^ti+p^tiTp^ti=∣∣p^si∣∣2+∣∣p^ti∣∣2−p^tiTRp^si−p^siTRTp^ti=∣∣p^si∣∣2+∣∣p^ti∣∣2−2p^tiTRp^si
拓展:向量的二范数为每个元素平方求和,且||v|| = v^T*v
可以证明对于旋转矩阵R, R T R = I R^TR=I RTR=I
同时,标量的转置等于自身,即 p ^ t i T R p ^ s i = p ^ s i T R T p ^ t i {\hat p_t^i}^T R {\hat p_s^i} = {\hat p_s^i}^T R^T {\hat p_t^i} p^tiTRp^si=p^siTRTp^ti
由于点的坐标都是确定的,也就是 ∣ ∣ p ^ s i ∣ ∣ 2 和 ∣ ∣ p ^ t i ∣ ∣ 2 ||{\hat p_s^i}||^2 和 ||{\hat p_t^i}||^2 ∣∣p^si∣∣2和∣∣p^ti∣∣2不变,所以最小化Loss就是最小化带R的那一部分,即:
R ∗ = arg min R ( − 2 ∑ i = 1 N p ^ t i T R p ^ s i ) R^{\ast} = \mathop{\arg\min}_{R} (-2 \sum_{i=1}^{N} {\hat p_t^i}^T R {\hat p_s^i}) R∗=argminR(−2i=1∑Np^tiTRp^si)
即:
R ∗ = arg max R ( ∑ i = 1 N p ^ t i T R p ^ s i ) R^{\ast} = \mathop{\arg\max}_{R} (\sum_{i=1}^{N} {\hat p_t^i}^T R {\hat p_s^i}) R∗=argmaxR(i=1∑Np^tiTRp^si)
我们可以得到:
∑ i = 1 N p ^ t i T R p ^ s i = t r a c e ( P t T R P s ) \sum_{i=1}^{N} {\hat p_t^i}^T R {\hat p_s^i} = trace(P_t^T R P_s) i=1∑Np^tiTRp^si=trace(PtTRPs)
其中 P t T 和 P s P_t^T和P_s PtT和Ps表示所有的点的 p ^ t 或 p ^ s \hat p_t或\hat p_s p^t或p^s,trace表示求矩阵的迹,trace中的三个矩阵为Nx3,3x3,3xN,相乘结果为NxN的矩阵,只有对角线上式对应某点的 p ^ t i T R p ^ s i {\hat p_t^i}^T R {\hat p_s^i} p^tiTRp^si。
所以问题转化为(问题向量化?):
R ∗ = arg max R t r a c e ( P t T R P s ) R^{\ast} = \mathop{\arg\max}_{R} trace(P_t^T R P_s) R∗=argmaxRtrace(PtTRPs)
根据trace(AB)=trace(BA):
t r a c e ( P t T R P s ) = t r a c e ( R P s P t T ) trace(P_t^T R P_s) = trace(R P_s P_t^T) trace(PtTRPs)=trace(RPsPtT)
之前令 H = ∑ i = 1 ∣ P s ∣ p ^ s i p ^ t i T H=\sum_{i=1}^{|P_s|}\hat p_s^i{\hat p_t^i}^T H=∑i=1∣Ps∣p^sip^tiT,即 H = P s P t T H=P_sP_t^T H=PsPtT,并对H进行SVD分解可以得到
t r a c e ( P t T R P s ) = t r a c e ( R P s P t T ) = t r a c e ( R H ) = t r a c e ( R U Σ V T ) = t r a c e ( Σ V T R U ) trace(P_t^T R P_s) = trace(R P_s P_t^T) \\ = trace(R H) \\ = trace(R U \Sigma V^T) \\ = trace(\Sigma V^T R U) trace(PtTRPs)=trace(RPsPtT)=trace(RH)=trace(RUΣVT)=trace(ΣVTRU)
其中V、R、U都是正交矩阵,所以 V T R U V^TRU VTRU也是正交矩阵。
令 M = V T R U = [ m 11 m 12 m 13 m 21 m 22 m 23 m 31 m 32 m 33 ] M = V^T R U = \left[ \begin{array}{cccc} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array} \right] M=VTRU=⎣⎡m11m21m31m12m22m32m13m23m33⎦⎤,则:
t r a c e ( Σ V T R U ) = t r a c e ( Σ M ) = σ 1 m 11 + σ 2 m 22 + σ 1 m 33 trace(\Sigma V^T R U) = trace(\Sigma M) \\ = \sigma_1 m_{11} + \sigma_2 m_{22} + \sigma_1 m_{33} trace(ΣVTRU)=trace(ΣM)=σ1m11+σ2m22+σ1m33
SVD拓展:一个mxn的矩阵A,分解为 A = U Σ V T A = U\Sigma V^T A=UΣVT,
SVD分解之后, Σ = [ σ 1 0 0 0 0 0 σ 2 0 0 0 0 0 ⋱ 0 0 0 0 0 ⋱ 0 ] m × n \Sigma = \left[ \begin{matrix} \sigma_1 & 0 & 0 & 0 & 0\\ 0 & \sigma_2 & 0 & 0 & 0\\ 0 & 0 & \ddots & 0 & 0\\ 0 & 0 & 0 & \ddots & 0\\ \end{matrix} \right]_{m\times n} Σ=⎣⎢⎢⎡σ10000σ20000⋱0000⋱0000⎦⎥⎥⎤m×n
UV均为单位正交阵
根据奇异值非负的性质和正交矩阵的性质,容易证得只有当 M 为单位阵时 trace(ΣM) 最大,即:
V T R U = I R = V U T V^T R U = I \\ R = V U^T VTRU=IR=VUT
所以最优的R为:
R ∗ = V U T R^{\ast} = V U^T R∗=VUT
最后还需要进行 Orientation rectification,即验证 R∗ 是不是一个旋转矩阵(检查是否有 |R|=1)
因为存在 |R|=−1 的可能,此时 R 表示的不是旋转而是一个 reflection,所以我们还要给上述优化求解加上一个 |R|=1 的约束。
在该约束下,M的行列式为:
∣ M ∣ = ∣ V T ∣ ∣ U ∣ ∣ R ∣ = ∣ V T ∣ ∣ U ∣ = ± 1 |M| = |V^T| |U| |R| \\ = |V^T| |U| = \pm 1 ∣M∣=∣VT∣∣U∣∣R∣=∣VT∣∣U∣=±1
如果 ∣ V U T ∣ = 1 |VU^T|=1 ∣VUT∣=1,则 ∣ M ∣ = 1 |M|=1 ∣M∣=1,此时 R ∗ = V M U T = V E U T = V U T R^{\ast} = VMU^T = VEU^T = V U^T R∗=VMUT=VEUT=VUT就是最优解。
如果 ∣ V U T ∣ = − 1 |VU^T|=-1 ∣VUT∣=−1,则 ∣ M ∣ = − 1 |M|=-1 ∣M∣=−1,我们需要求解此时的R,也就是求解 ∣ M ∣ = − 1 |M|=-1 ∣M∣=−1时 什么样的M能让trace(ΣM)最大。 https://www.math.pku.edu.cn/teachers/yaoy/Fall2011/arun.pdf(详细讨论),链接中的结论为:让trace(ΣM)最大的M为:
M = [ 1 0 0 0 1 0 0 0 − 1 ] M = \left[ \begin{array}{cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{array} \right] M=⎣⎡10001000−1⎦⎤
将上面两种情况综合起来:
R ∗ = V [ 1 0 0 0 1 0 0 0 ∣ V U T ∣ ] U T R^{\ast} = V \left[ \begin{array}{cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & |V U^T| \end{array} \right] U^T R∗=V⎣⎡10001000∣VUT∣⎦⎤UT
可以保证最优的R*行列式始终为1
总结:最优变换步骤
- 计算源点云和目标点云质心;
- 将源点云和目标点云转换到质心坐标系;
- 计算矩阵 H(形式类似“协方差矩阵”);
- 对 H 求 SVD 分解,根据公式求得 R∗;
- 根据公式计算 t∗。
ICP算法关键点:
(1)原始点集的采集
均匀采样、随机采样和法矢采样
(2)确定对应点集
点到点、点到投影、点到面
(3)计算变化矩阵
四元数法、SVD奇异值分解法
迭代
每一次迭代都会得到当前的最优变换参数 R k , t k R_k,t_k Rk,tk
然后把这个变换作用于源点云,产生新的临时变换目标点云 P t _ k P_{t\_k} Pt_k,继续找源点云和目标点云之间的最近对应点
“找最近对应点”和“求解最优变换”这两步不停迭代进行,
直到满足迭代终止条件(阈值判断),常用的终止条件有:
- R k , t k R_k,t_k Rk,tk 的变化量小于一定值
- loss 变化量小于一定值
- 达到最大迭代次数
优缺点和改进
ICP 优点:
- 简单,不必对点云进行分割和特征提取
- 初值较好情况下,精度和收敛性都不错
ICP 缺点:
- 找最近对应点的计算开销较大
- 只考虑了点与点距离,缺少对点云结构信息的利用
原始的 ICP 算法采用最小二乘估计变换矩阵,原理简单,精度较好,但是由于采用迭代计算,计算开销大,速度较慢,对初始变换敏感(依赖于初始的变换,初始变换找的好坏,会很大程度影响结果),容易陷入局部最优解。
原始的ICP可以看做为Point-to-Point ICP
自 ICP 提出以来,有相当多的 ICP 改进算法
- Point-to-Plane ICP,原始 ICP 算法的代价函数中使用的 point-to-point 距离,point-to-plane 则是考虑源顶点到目标顶点所在面的距离,比起直接计算点到点距离,考虑了点云的局部结构,精度更高,不容易陷入局部最优;但要注意 point-to-plane 的优化是一个非线性问题,速度比较慢,一般使用其线性化近似;
- Plane-to-Plane ICP,point-to-plane 只考虑目标点云局部结构, plane-to-plane 顾名思义就是也考虑源点云的局部结构,计算面到面的距离;
- Generalized ICP (GICP),综合考虑 point-to-point、point-to-plane 和 plane-to-plane 策略,精度、鲁棒性都有所提高;
- Normal Iterative Closest Point (NICP),考虑法向量和局部曲率,更进一步利用了点云的局部结构信息,其论文中实验结果比 GICP 的性能更好。
注意事项
- ICP 比较依赖于变换初值,平移比较简单,直接用点云质心来估计;旋转初值的话可以手动调一个粗略值,或者沿每个轴的旋转进行采样、组合来尝试(不适合实时性应用);
- 点太多的话可以先降采样;
- 找到一些 anchor 点对(比如先用特征点匹配),可以帮助加速收敛;
- 对应用场景引入一些合理假设,比如限制旋转、平移的范围,变换自由度数量等。
ICP变种
普通的ICP在计算点与点之间的误差、代价函数时,使用点对点的距离作为误差。
PL-ICP(Point-to-Line):
相对于PP-ICP最大的区别就是改进了误差方程。
将点对点的距离 改成 点到其最近两个点连线的距离。精度更高。
Point-to-Plane ICP
误差方程中考虑的是源顶点到目标顶点所在面的距离,考虑目标点云的局部结构
Plane-to-Plane ICP,
point-to-plane 只考虑目标点云局部结构, plane-to-plane 顾名思义就是也考虑源点云的局部结构,计算面到面的距离;
GICP(Generalized ICP )
综合考虑 point-to-point、point-to-plane 和 plane-to-plane 策略,精度、鲁棒性都有所提高;
NICP(Normal)
考虑在误差方程中加入法向量和曲率
粗配准
ICP算法的基本原理。它需要一个旋转平移矩阵的初值。这个初值如果不太正确,那么由于它的greedy优化的策略,会使其目标函数下降到某一个局部最优点(当然也是一个错误的旋转平移矩阵)。因此,我们需要找到一个比较准确的初值,这也就是粗配准需要做的。
粗配准目前来说还是一个难点。针对于不同的数据,有许多不同的方法被提出。
配准的评价标准:
比较通用的一个是LCP(Largetst Common Pointset)
给定两个点集P,Q,找到一个变换T§,使得变换后的P与Q的重叠度最大。
在变换后的P内任意一点,如果在容差范围内有另外一个Q的点,则认为该点是重合点。
重合点占所有点数量的比例就是重叠度。
解决上述LCP问题,最简单粗暴的方法就是遍历。
假设点集P,Q的大小分别为m,n。
而找到一个刚体变换需要3对对应点。那么brute force 搜索的需要 O ( m 3 n 3 ) O(m^3n^3) O(m3n3)的复杂度。对于动辄几百万个点的点云,这种时间复杂度是不可接受的。
因此,许多搜索策略被提出。
搜索策略
比较容易想到的是RANSAC之类的搜索方法。而对于不同的场景特点,可以利用需配准点云的特定信息加快搜索。(例如知道点云是由特定形状的面构成的)这里先介绍一个适用于各种点云,不需要先验信息的搜索策略,称为4PC(4 Point Congruent)。
4PC(4 Point Congruent):
4PC搜索策略是在P,Q中找到四个共面的对应点。

四个共面的点相交于e
有两个比例在刚体变化下是不变的。 ∣ a e ∣ / ∣ e b ∣ = ∣ a ′ e ′ ∣ / ∣ e ′ b ′ ∣ |ae|/|eb|=|a'e'|/|e'b'| ∣ae∣/∣eb∣=∣a′e′∣/∣e′b′∣ 和 ∣ d e ∣ / ∣ e c ∣ = ∣ d ′ e ′ ∣ / ∣ e ′ c ′ ∣ |de|/|ec|=|d'e'|/|e'c'| ∣de∣/∣ec∣=∣d′e′∣/∣e′c′∣(实际上在仿射变换下也是不变的。)
4PC将对于三个点的搜索转换为对e,e’的搜索,从而将复杂度降低到了 O ( n 2 + k ) O(n^2+k) O(n2+k)。这四个点的距离越远,计算得到的转换越稳健。但是这里的四个点的搜索依赖于两个点云的重叠度。
4PC算法通用性较好,但是对于重叠度较小、或是噪声较大的数据也会出现配准错误或是运行时间过长的问题。
具体的算法:4-Points Congruent Sets for Robust Pairwise Surface Registration
参考:
https://www.zhihu.com/question/34170804