神经网络裁剪技术 ------ 显著性(Distinctiveness)
前言
随着深度学习技术的不断发展,其逐步应用到愈发复杂的现实背景当中。为了处理复杂的现实问题,人们所使用的神经网络模型变得越来越深(隐藏层 hidden layer 数目增加),亦或者是越来越大(单个隐藏层内包含的隐藏神经元 hidden unit 的数量增加),从而导致了计算量增加,计算时间增加,以及参数占用的内存增加。为了控制模型的大小,人们使用各种方法尽可能减少参数的使用,比如减少隐藏层数目或者减少单个隐藏层中隐藏神经元的数目,但隐藏单元的减少意味着减少该模型可能从输入数据中提取到的特征数目(每一个隐藏神经元的作用可认为是提取一个独立的特征)。
一开始选择适当的模型结构以及隐藏单元的数目往往取决于设计者的经验,并没有固定准确的方法可供参考。因此,人们通常会将神经网络设计成稍大一点,以保证拥有足够或者过多的参数提取必要的特征,即便这种方法存在着过拟合的风险。本文将介绍一种网络裁剪技术,可用于除去已训练深度神经网络的冗余参数,从而得到规格相对较小,又能保证特征提取的模型,该方法也可用于预实验,为深度神经网络模型的结构设计提供参考。
需要说明的是,本文的实验是根据 T. Gedeon 和 D. Harris 的论文 Network reduction techniques 介绍的方法进行的,有兴趣的朋友可以阅读文末提供的参考文献。
原理说明
要介绍如何利用显著性(Distinctiveness)对神经网络进行裁剪,我们先简单复习以下神经网络的基本内容。
神经网络结构
上图是一个简单的三层神经网络(3-layer Neural Network)或者也叫两层神经网络(2-hidden-layer Neural Network)。它有三个网络层,分别是输入层(input layer)、隐藏层(hidden layer)和输出层(output layer),其大小分别为3、5和2。对于这个模型,我们可以简单的理解就是,它有一个隐藏层,可以提取输入样本中简单的或者说低维度的特征,比如直线、曲线之类的。隐藏层中具有5个隐藏神经元,可以认为它们分别提取不同的简单特征。
但是,如果输入层接收到样本是一个极其简单的对象,隐藏层中可能只需2个或者3个神经元,模型就能得到很好的结果,而5个隐藏单元则会导致冗余,可能某两个或三个单元提取了同一个特征,增加了运算量和运算时间,甚至还会造成过拟合。那在这种情况下,我们就可以参考每个隐藏单元的显著性(Distinctiveness)来决定,如何确定模型的大小,以及保留哪些隐藏层的神经元。
向量角分析
向量角分析是判断隐藏单元显著性(Distinctiveness)的方法之一。多个输入样本在隐藏层的输出结果可构成一个矩阵,本文所设计的神经网络在隐藏层使用 Sigmoid 作为激活函数,该激活函数的输出值在 0 ~ 1的范围内,为了便于后面的向量角分析,我们对其输出结果添加一个 -0.5 的偏移量,使其范围变成 -0.5 ~ 0.5,原因会在后文进行解释。下表是输入5个样本在同一隐藏层得到的输出结果:
| 神经元1 | 神经元2 | 神经元3 | 神经元4 | 神经元5 | |
| 1 |
0.499895692 | 0.481001914 | -0.436968148 | -0.300517321 | -0.365247995 |
| 2 | 0.411050916 | 0.057419121 | 0.4929986 | 0.030264854 | 0.262811184 |
| 3 |
-0.094105452 | 0.15255636 | 0.476602495 | -0.10142675 | 0.128765941 |
| 4 | 0.056025863 | -0.176585108 | 0.457032502 | 0.103210866 | 0.494007826 |
| 5 | -0.350434244 | 0.456910014 | -0.498010606 | -0.348486006 | 0.499998927 |
根据前文对神经网络隐藏单元的介绍,同一个隐藏神经元在不同的样本中会提取相同的特征,不同的隐藏单元针对同一个输入样本,应该提取的是不同的特征。向量角分析就是分析不同隐藏神经元对在相同输入样本时输出结果的相似性,也就是分析上表中每一列数据的向量角大小,从而判断其相似性。相似的两列数据说明对应的两个隐藏神经元提取类似的特征,其作用的相似的,因此可以将他们合并;完全相反的两列数据说明对应的两个隐藏神经元的结果相互抵消,因此可以同时将它们删去。
向量角的计算公式为:angle(u, v) = arccos (u ⋅ v / (∥ u ∥ ⋅ ∥ v ∥)
u 和 v 分别代表两个向量,对应上表中某两列的数据。根据反余弦函数的定义(arccos),其输出结果范围是 0 ~ 180 度。由于 Sigmoid 的输出范围是 0 ~ 1,因此所有值都为整数的两个向量间的向量角必然在 0 ~ 90 度之间,为了得到 90 ~ 180 度的结果,我们给激活函数 Sigmoid 的结果添加一个 -0.5 的偏移量,这样才会出现负数值,计算得到的向量角才会覆盖 90 ~ 180 度的范围。
计算出向量角后,一般的处理规则是:向量角小于15度的两个向量,我们认为其作用的相似的,也就是说它们满足线性相关,所以可以删去其中一个隐藏单元,并把它的参数(weight 和 bias)加到另一个隐藏单元中;向量角大于165度的两个向量,我们认为其作用是相斥的,其作用在计算过程中相互抵消,所以可以直接删去这两个隐藏神经元。
当一个隐藏层较大时,也是一个隐藏层包含很多隐藏神经元时,可以会出现多个隐藏神经元两两之间满足向量角小于15度的条件。在这种情况下,可以优先选择向量角最小的两组进行合并。另一种比较严谨的处理方法是,依次尝试合并任意两个隐藏神经元,再对比每一个裁剪后模型的结果,选择结果最优的那一组隐藏神经元进行合并。而对于多个隐藏神经元两两之间满足向量角大于165度的情况,可以选择向量角最大的两组进行合并。
实验结果
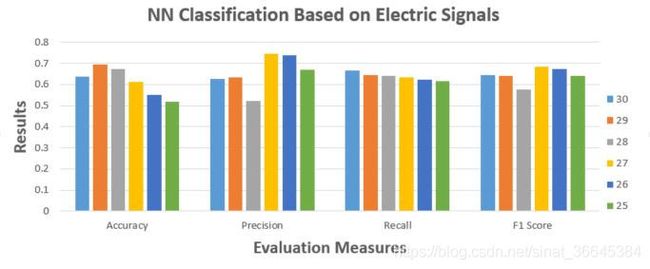
本文的实验采用论文 Melodious Micro-frissons: Detecting Music Genres From Skin Response 提供的数据和模型进行裁剪,针对两组不同的数据集得到分别得到以下的结果:
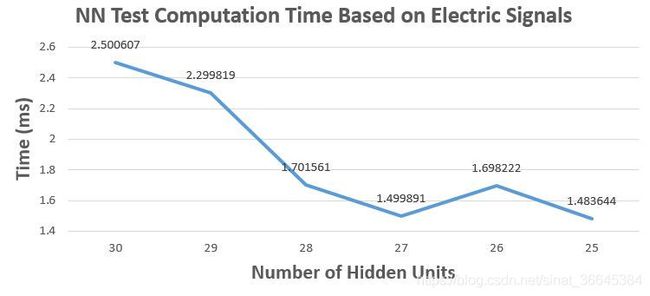
上述实验是将一个三层神经网络(输入层大小为11, 隐藏层大小为30, 输出层大小为3)通过分析 Distinctiveness 后合并隐藏单元,对模型进行裁剪过程中,计算各种指标的结果。第一个图分别对比了裁剪后模型的准确率(Accuracy)、精确率(Precission)、召回率(Recall)和 F1 分值,第二个图展示了裁剪后模型计算相同测试集所花费的时间。可以看出,裁剪后的模型在各个指标上基本能保持和原始模型相似的结果,一个明显的改善是,随着模型的裁剪,计算时间基本在逐步减小。
总结
通过上述的方法,我们可以看出,裁剪后的模型能基本保持原来的性能,并在此基础上减少了参数的数量,节省了存储空间以及减少了计算的时间。该技术既能在原有模型的基础上去除冗余的隐藏神经元,又可以在设计神经网络过程中针对给定数据集提供参考的隐藏单元设计。值得指出的是,隐藏神经元的处理是局限于同一个隐藏层的所有神经元,不是同一层的隐藏单元不能用于上述方法。而上文提及的处理过程中,并未对裁剪后得到的新模型进行重训练。在实际应用中,可以使用相同的训练集对裁剪后的模型进行重训练,一般来说可以使模型对数据的拟合度稍微得到提升。
参考文献
J. Rahman, T. Gedeon, S. Caldwell, R. Jones, M. Hossain, and X. Zhu, "Melodious Micro-frissons: Detecting
Music Genres From Skin Response," in In 2019 International Joint Conference on Neural Networks (IJCNN),
2019: IEEE, pp. 1-8.
T. Gedeon and D. Harris, "Network reduction techniques," in Proceedings International Conference on Neural
Networks Methodologies and Applications, 1991, vol. 1, pp. 119-126.