pytorch稀疏张量模块torch.sparse详解
torch.sparse是一个专门处理稀疏张量的模块。通常,张量会按一定的顺序连续地进行存取。但是,对于一个存在很多空值的稀疏张量来说,顺序存储的效率显得较为低下。因此,pytorch推出了稀疏张量的处理模块。在这里,有意义的值被称为specified elements,而无意义的值(空值,通常为0,但是也可以是其他值)则被称为fill value。只有足够稀疏的张量使用这种方式进行存储才能获得更高的效率。稀疏张量的表示方式有多种,比如COO、CSR/CSC、LIL等,下面介绍COO和CSR两种格式。
1 Sparse COO Tensor
1.1 Coordinate format
这种格式的稀疏矩阵是通过indices和values两个张量共同存储的,其中indices张量存储的是specified elements的坐标值,维度为(ndim, nse),类型为torch.int64;values张量存储的是specified elements的值,维度为(nse,)。其中,ndim是张量的维度,nse是specified elements的个数。
下面举个例子演示如何使用torch.sparse_coo_tensor()函数来构造一个COO稀疏矩阵,以及通过to_dense()方法将其变为一般的张量。其中3位于(0, 2)位置,4位于(1, 0)位置,5位于(1, 2)位置。
>>> i = [[0, 1, 1],
[2, 0, 2]]
>>> v = [3, 4, 5]
>>> s = torch.sparse_coo_tensor(i, v, (2, 3))
>>> s
tensor(indices=tensor([[0, 1, 1],
[2, 0, 2]]),
values=tensor([3, 4, 5]),
size=(2, 3), nnz=3, layout=torch.sparse_coo) # nnz指specified elements个数
>>> s.to_dense()
tensor([[0, 0, 3],
[4, 0, 5]])
上述例子中,i的第一行表示第一维坐标值,第二行表示第二维坐标值。i也可以使用坐标对来表示,但是在构造稀疏矩阵时,需要将i进行转置,如下:
>>> i = [[0, 2], [1, 0], [1, 2]]
>>> v = [3, 4, 5 ]
>>> s = torch.sparse_coo_tensor(list(zip(*i)), v, (2, 3))
>>> # Or another equivalent formulation to get s
>>> s = torch.sparse_coo_tensor(torch.tensor(i).t(), v, (2, 3))
>>> torch.sparse_coo_tensor(i.t(), v, torch.Size([2,3])).to_dense()
tensor([[0, 0, 3],
[4, 0, 5]])
一个空的稀疏COO张量可以通过如下方式进行构造:
>>> torch.sparse_coo_tensor(size=(2, 3))
tensor(indices=tensor([], size=(2, 0)),
values=tensor([], size=(0,)),
size=(2, 3), nnz=0, layout=torch.sparse_coo)
1.2 Hybrid sparse COO tensors
上面的例子中,每个坐标下的值都是一个标量(零维数据)。但其实也可以是一个多维的数据,这一拓展的数据被称为Hybrid sparse COO tensors。在这里,indices张量的维度为(sparse_dims, nse),values张量的维度为(nse, dense_dims)。记sparse_dims的大小为M,dense_dims的大小为K,则这个hybrid张量的维度为N=M+K。
举个例子,下面构造一个sparse_dims为2、dense_dims为1的三维hybrid张量。其中[3, 4]位于(0, 2),[5, 6]位于(1, 0),[7, 8]位于(1, 2)。
>>> i = [[0, 1, 1],
[2, 0, 2]]
>>> v = [[3, 4], [5, 6], [7, 8]]
>>> s = torch.sparse_coo_tensor(i, v, (2, 3, 2))
>>> s
tensor(indices=tensor([[0, 1, 1],
[2, 0, 2]]),
values=tensor([[3, 4],
[5, 6],
[7, 8]]),
size=(2, 3, 2), nnz=3, layout=torch.sparse_coo)
>>> s.to_dense()
tensor([[[0, 0],
[0, 0],
[3, 4]],
[[5, 6],
[0, 0],
[7, 8]]])
记M = s.sparse_dim(),K = s.dense_dim(),有如下关系成立:
M + K == len(s.shape) == s.ndim
s.indices().shape == (M, nse)
s.values().shape == (nse,) + s.shape[M : M + K]
s.values().layout == torch.strided
1.3 Uncoalesced sparse COO tensors
COO稀疏张量又可以分为两种:uncoalesced和coalesced。其中uncoalesced允许同一个索引下存在多个不同的值,而coalesced则不行。它们之间可以相互转换,例子如下:
>>> i = [[1, 1]]
>>> v = [3, 4]
>>> s=torch.sparse_coo_tensor(i, v, (3,))
>>> s
tensor(indices=tensor([[1, 1]]),
values=tensor( [3, 4]),
size=(3,), nnz=2, layout=torch.sparse_coo)
>>> s.is_coalesced()
False
>>> s.coalesce()
tensor(indices=tensor([[1]]),
values=tensor([7]),
size=(3,), nnz=1, layout=torch.sparse_coo)
>>> s.is_coalesced()
True
上述例子说的是,在索引1处存在3和4两个值,而将其coalesce后,则相同索引的值会被相加合并,它们可以通过is_coalesced()方法进行判断。这两种形式并不存在优劣之分,通常也不必太在意它们是哪种方式。在有些情况下uncoalesced效率高,而在有些情况下coalesced效率高。但是,如果你在重复进行一些会产生重复值的操作(比如torch.Tensor.add())时,需要时常将稀疏张量进行coalesce,不然结果会变得非常大。
1.4 Working with sparse COO tensors
下面是COO稀疏张量运算的示例。首先,构建一个如下稀疏张量:
>>> i = [[0, 1, 1],
[2, 0, 2]]
>>> v = [[3, 4], [5, 6], [7, 8]]
>>> s = torch.sparse_coo_tensor(i, v, (2, 3, 2))
对张量类型进行判断:
>>> isinstance(s, torch.Tensor)
True
>>> s.is_sparse
True
>>> s.layout == torch.sparse_coo
True
获得其sparse_dim和dense_dim()的值:
>>> s.sparse_dim(), s.dense_dim()
(2, 1)
获得indices和values张量,coalesced和uncoalesced的方式不一样:
# coalesced
>>> s.indices()
tensor([[0, 1, 1],
[2, 0, 2]])
>>> s.values()
tensor([[3, 4],
[5, 6],
[7, 8]])
# uncoalesced
>>> s._indices()
tensor([[0, 1, 1],
[2, 0, 2]])
>>> s._values()
tensor([[3, 4],
[5, 6],
[7, 8]])
也就是说uncoalesced需要前面加一个_,否则会报错。
切片操作。COO稀疏张量仅支持dense维度上的切片操作,也即其实是将稀疏表示的张量转换成一般表示的张量之后再执行的切片操作的结果。举个例子:
>>> s[1]
tensor(indices=tensor([[0, 2]]),
values=tensor([[5, 6],
[7, 8]]),
size=(3, 2), nnz=2, layout=torch.sparse_coo)
>>> s[1, 0, 1]
tensor(6)
>>> s[1, 0, 1:]
tensor([6])
下面分析一下上述代码的输出结果,只要将s转成dense表示的张量,就明白了:
>>> s.to_dense()
tensor([[[0, 0],
[0, 0],
[3, 4]],
[[5, 6],
[0, 0],
[7, 8]]])
其中,s[1]的values输出结果也即to_dense()之后结果的下半部分,当然是不包括空值的。然后indices输出结果0和2则是:(1, 0)对应值[5, 6]的坐标,(1, 2)对应值[7, 8]的坐标。
2 Sparse CSR Tensor
CSR (Compressed Sparse Row)格式只支持二维张量的存取,不支持多维张量。但是,与COO格式相比,它有更高的空间存储效率以及更快的运算速度。它由三个一维张量组成:crow_indices、col_indices和values。其中,crow_indices用于存储行索引,它的大小为size[0]+1,其中最后一个数字记录了稀疏矩阵中包含多少个specified elements;col_indices记录了每个specified elements的列索引,其大小为nnz(即specified elements个数);values记录的则是每个specified elements的具体值,大小也为nnz。
可以通过torch.sparse_csr_tensor()方法来构造一个CSR稀疏张量,需要给出crow_indices、col_indices和values三个张量,其中crow_indices最后一个指示specified elements个数的数字可以省略,将被自动计算。一个示例:
>>> crow_indices = torch.tensor([0, 2, 4])
>>> col_indices = torch.tensor([0, 1, 0, 1])
>>> values = torch.tensor([1, 2, 3, 4])
>>> csr = torch.sparse_csr_tensor(crow_indices, col_indices, values, dtype=torch.double)
>>> csr
tensor(crow_indices=tensor([0, 2, 4]),
col_indices=tensor([0, 1, 0, 1]),
values=tensor([1., 2., 3., 4.]), size=(2, 2), nnz=4,
dtype=torch.float64)
>>> csr.to_dense()
tensor([[1., 2.],
[3., 4.]], dtype=torch.float64)
此外,也可以通过tensor.to_sparse_csr()方法将一个普通张量或者是COO稀疏张量转换为一个CSR稀疏张量,其中的0值将被视为fill elements,如下所示:
>>> a = torch.tensor([[0, 0, 1, 0], [1, 2, 0, 0], [0, 0, 0, 0]], dtype = torch.float64)
>>> sp = a.to_sparse_csr()
>>> sp
tensor(crow_indices=tensor([0, 1, 3, 3]),
col_indices=tensor([2, 0, 1]),
values=tensor([1., 1., 2.]), size=(3, 4), nnz=3, dtype=torch.float64)
目前pytorch仅支持CSR稀疏张量的tensor.matmul()运算:
>>> vec = torch.randn(4, 1, dtype=torch.float64)
>>> sp.matmul(vec)
tensor([[0.9078],
[1.3180],
[0.0000]], dtype=torch.float64)
3 Appendix
3.1 Supported Linear Algebra operations
下表总结了稀疏矩阵上支持的线性代数运算。这里,T[layout]表示具有给定布局的张量。类似地,M[layout]表示矩阵(2-D PyTorch张量),V[layout]表示向量(1-D PyTorch张量)。此外,f表示标量(float或0-D PyTorch张量),*表示元素乘法,@表示矩阵乘法。下表中,Sparse grad?一列指示了该运算是否支持稀疏张量的反向传播梯度计算。
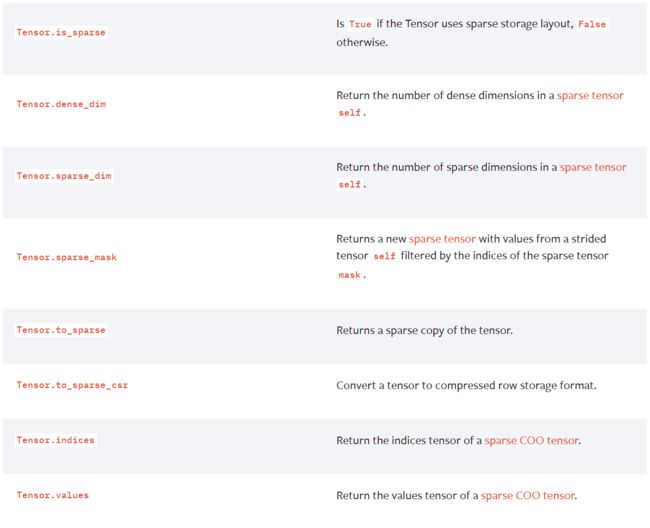
3.2 Tensor methods and sparse
下表是与稀疏张量相关的方法:
3.3 Torch functions specific to sparse Tensors
下表是只支持稀疏张量的方法: