深度学习-----学习笔记（一）（修仙~~~ing）

---

前言

凡我不能创造的，我就不能理解。 ----------理查德.费曼

一、机器学习、深度学习及神经网络的简单概述及关系

机器学习、深度学习和神经网络都是人工智能的子领域。而深度学习是机器学习的一个子领域，神经网络则是深度学习的一个子领域。
##########################################################################################################

1. 机器学习

  机器学习是一门人工智能的科学，该领域的主要研究对象是人工智能，特别是如何在经验学习中改善具体算法的性能。是用数据或以往的经验，以此优化计算机程序的性能标准。

  机器学习针对两类问题：“分类问题”与“回归问题”。

   (1). 分类问题： 数据属于哪个类别的问题。 eg：一张人像，判断这张照片中这个人是男是女。
   (2). 回归问题： 根据一个输入预测一个数值。eg：一张人像，判断他的体重、身高。

  机器学习问题步骤可分为两个阶段：“学习（训练）” 与 “推理”。首先，在学习阶段进行模型的学习（得到合适的参数，eg：权重、偏置等。），之后在推理阶段用学习到的模型对未知的数据进行处理。
##########################################################################################################

2. 深度学习

   深度学习是学习样本数据的内在规律和表示层次，这些学习过程中获得的信息对诸如文字，图像和声音等数据的解释有很大的帮助。它的最终目标是让机器能够像人一样具有分析学习能力，能够识别文字、图像和声音等数据。 深度学习是一个复杂的机器学习算法，在语音和图像识别方面取得的效果，远远超过先前相关技术。深度学习在搜索技术，数据挖掘，机器学习，机器翻译，自然语言处理，多媒体学习，语音，推荐和个性化技术，以及其他相关领域都取得了很多成果。深度学习使机器模仿视听和思考等人类的活动，解决了很多复杂的模式识别难题，使得人工智能相关技术取得了很大进步。
（上段来自百度百科定义。）
   最近十几年来，随着NVIDIA 推出 CUDA 这一通用并行计算架构使 GPU 能够解决复杂的计算问题。在利用分布式学习可以更快的缩短学习时间。例如Google的TensorFlow、微软的CNTK这些支持多GPU或者多机器的分布式学习框架。自此后我们就有能力处理庞大的数据量，斯坦福大学教授李飞飞为了解决机器学习中过拟合和泛化的问题而牵头构建的ImageNet数据集更是一大助力。自从2012年举办的大规模图像识别大赛ILSVRC(ImageNet Large Scale Visual Recognition Challenge)中基于深度学习的方法（AlexNet）以压倒性的优势胜出后，以往的图像识别方法就被颠覆了。深度学习开始活跃在舞台中央。
##########################################################################################################

3. 神经网络

  简单来说神经网络就是一个函数。它们都是将某些输入变换为输出的变换器。神经网络是深度学习的基础，如图1所示就是一个简单的3层神经网络。它分为三层，输入层、隐藏层（中间层）、输出层。又因为所有相邻的神经元之间都存在由箭头表示的连接，所以图一也可称为全连接网络（相邻的所有神经元之间都有连接称为全连接）。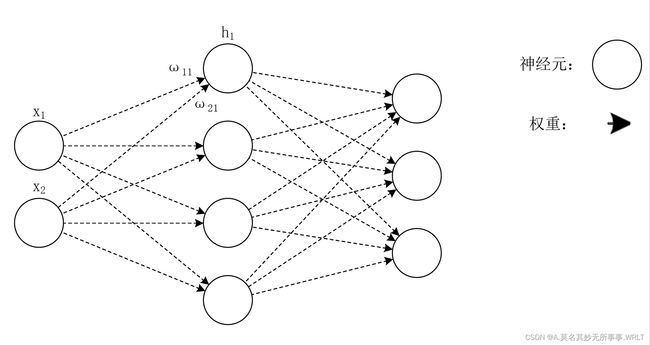
                              图1
  在图一中我们使用O来表示神经元（人工神经网络中最基础的计算单元），而箭头表示它们之间的连接。箭头上有权重设为ω。这个权重和对应的神经元的值分别相乘，其和（严格来说，是经过激活函数变换后的值）作为下一个神经元的输入。此外还需要加上一个不受迁移层神经元影响的常数，这个常数称为偏置设为b。（图上没标注出来）
  数学式表示为： $$\ast \ast h_1=x_1{\omega }_{11}+x_2{\omega }_{21}+b_1\ast \ast$$

  式子中h1代表隐藏层中第一个神经元，x1则是输入层的第一个神经元，ω11和ω21分别是输入层的两个神经元连接的权重（箭头），b1是加上的常数偏置。这样就可以求出所有隐藏层神经元的值。
  此式子可以简化为$$\ast \ast h=xW+b\ast \ast$$
  全连接层的变换是线性变换。而激活函数赋予它“非线性”的效果。严格来讲，使用非线性的激活函数可以增强神经网络的表现力。简单来说，就是非线性的激活函数插入到线性的全连接层中去可以让网络更为贴合实际。但是全连接层(Affine层)没有考虑到数据传输时数据的形状，它把3维的图像数据通过仿射变换（矩阵相乘）拉平为1维数据进行运算。这样做无法使用形状的某些空间信息。eg:空间上邻近的像素为相似的值、相距较远的像素没什么关联等。但在原有的全连接层(Affine层)的基础上加入卷积层和池化层就可以解决这种问题。而加入了“卷积层”和“池化层”的网络被称为CNN（卷积神经网络）。在图像处理领域，使用的多是CNN。
  CNN上个世纪就被提了出来，自2012年ILSVRC后，有越来越多，错误识别率越来越低的优秀算法。几种典型的如下：

（1）.LeNet (1998)它是CNN元祖，进行手写数字识别的网络。它有连续的卷积层和池化层，最后由全连接层输出结果。激活函数使用的是Sigmoid函数。使用子采样缩小中间数据大小。
（2）. Alex Net（2012）Alex Net有多个卷积层和池化层，最后由全连接层输出结果。使用ReLU作为激活函数使用了局部正规化的LRN层和Dropout(一种在学习的过程中随即删除神经元的方法。在学习过程中随即删除神经元。从而让每个不同的模型进行学习，然后在推理时，通过对神经元的输出乘以删除比例取模型的平均值)。16.4%的错误识别率。
（3）. VGG（2014）结构简单、应用性强。它由卷积层和池化层构成的基础的CNN，特点是将有权重的层（卷积层或全连接层）叠至16层（19层），具备了深度。卷积层使用3X3的小型滤波器，插入池化层逐步减小中间数据的空间大小。激活函数使用ReLu函数。大约7.3%的错误识别率。
（4）. GoogLeNet（2014）GoogleNet不仅在纵向上有深度，在横向上还有‘宽度’，称为Inception结构，加入了1X1的卷积运算。大约6.7%的错误识别率。
（5）. ResNet（2015）过度加深层数也会导致很多学习不能进行。为了解决这个问题，导入了“快捷结构”来跳过一定数量的层避免层数过多引起的梯度变化。大约3.5%的错误识别率。
  以上几种网络都不断加深层的深度，随着层次加深，神经元从简单的形状向‘高级’信息变化，响应的对象也在逐渐变化。这样做有以下几个好处：

（1）. 减少参数的网络数量。（用更小的参数达到同等水平的表现力）
（2）. 使学习更加高效。（分层解决问题）
但与此同时，也不能一昧的增加神经网络的深度，否则会导致很多学习无法正常进行。

神经网络的推理所进行的处理相当于神经网络的正向传播。（正向推理（利用学习得到的合适的参数进行对未知的模型的推理。））
神经网络的学习所进行的处理相当于神经网络的反向传播。（反向学习（利用梯度来选取合适的参数（权重、偏置等））
  在开始学习时，权重、偏置等初始值的设定也需要考虑到，一般Sigmoid激活函数和tanh函数选用Xavier初始值（√1/n），ReLu函数选用He初始值（√2/n）。并且虽然我们的最终目的是提高识别精度，但在学习的过程中，我们却引入了另一个判断的依据----损失函数（损失函数是用来表示神经网络性能的“恶劣程度”的指标，这个损失函数可以使用任意函数，但一般使用均方误差和交叉熵误差等。），那为什么用损失函数，而不直接使用识别精度呢？
  因为为了提高识别精度，就要通过梯度来更新参数（权重、偏置）的值。而识别精度却对微小参数值的变化没反应。就是说使用识别精度，其参数的导数在绝大多数地方会变为0。所以神经网络中使用Sigmoid等非线性激活函数（导数在任何地方都不为0），而不像感知机使用阶跃函数。
  而为了寻找合适的参数（权重、偏置），有很多方法，几种如下：
（1）.SGD（随机梯度下降法）
（2）.Momentum（动量）
（3）.AdaGrad(学习率)
（4）.Adam
  而误差反向传播法可以高效求参数的梯度。
  同时我们在处理庞大的数据量时，通常采用“多批量”的方法。就是通过关注输入数据和权重参数的“形状”，通过矩阵相乘来一次性处理多张照片。这样做可以大幅缩短每张图像的处理时间。
  就笔者现在所学而言，神经网络的目的就是不断贴合实际，通过叠加或者变换层数等手段以求得到智能。
##########################################################################################################

二、从感知机开始

  感知机由美国学者FrankRosenblatt在1957年提出。是神经网络的起源算法。

1.感知机是什么？

  感知机接收多个输入信号，输出一个输出信号。它的信号只有1/0两种取值。
  我们将多个输入信号设为x1、x2等，将输出信号记为y。在设有权重ω1、ω2，用输入分别乘以权重，再相加。这个数学式就可以判断出输出y的值。如下式：

$$y=\{\begin{array}{rl}0(& \omega x_1+\omega x_2\le \Theta )\\ 1(& \omega x_1+\omega x_2>\Theta )\end{array}$$
  在这个式子中，Θ被称为阈值，就是说只有在输入信号乘上权值后的值相加>阈值后，才会输出1，此时神经元被激活。
  所以说，权重越大，对输入信号影响就越大，输出信号就越大。

2.我们人要做什么？我们又需要让机器学习什么？

  如二.1所言，我们需要确定权重参数ω，而机器学习的课题就是让计算机去算出ω。学习是确定合适的参数的过程，而人要做的是思考感知机的构造（模型），并把训练数据交给计算机。

3.感知机的实现

  如下，定义一个接受参数x1和x2的AND函数（此时人为设定了权值）

def AND(x1, x2):
	w1, w2, theta = 0.5, 0.5, 0.7
	tmp = x1*w1 + x2*w2
	if tmp <= theta:
		return 0
	elif tmp > theta:
		return 1

  上面的代码其实就是求输出信号y。
  接下来我们可以将Θ用-b替换，就可以得到如下的式子：
$$y=\{\begin{array}{rl}0(& \omega x_1+\omega x_2+b\le 0)\\ 1(& \omega x_1+\omega x_2+b>0)\end{array}$$
  此时，称x为权重，b为偏置。感知机会计算输入信号与权重的乘积，再加上偏置，如果这个值>0输出1，否则输出0。
按这个思路可以通过改变权重实现简单逻辑电路与、与非、或、或非门（其实就是对着这几种门电路的真值表设计）。但异或门却无法完成（异或门的真值表按照00、01、10、11的顺序是0、1、1、0。在图2里X\Y轴上的坐标就是两个输入信号，而输出就是异或后的值。）。
因为对于与、与非、或门、或非而言，图形具是线性（可以用一根直线将输出0、1完全隔开），而对于异或而言，需要用曲线（非线性）来隔开。如下图2

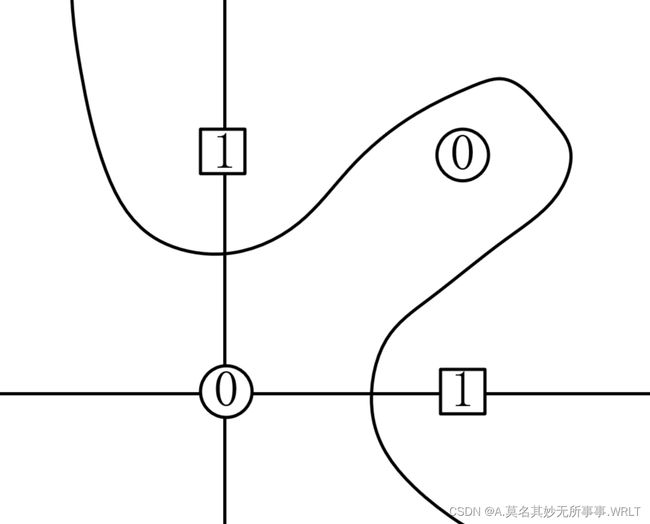
                              图2

---

  那么如何解决这个问题呢？
  换个思路，我们可以在我可用些数电的知识，异或门的结果其实就是与非门和或门的与门。
  所以接下来我们可以这么定义：

def XOR(x1, x2):
	s1 =NAND(X1,X2)
	s2 =OR(X1,X2)
	y = AND(s1,s2)
	return y

  那么这种做法是不是相当于在X（输入）和Y（输出）中间又加了一层（与非门和或门）。此时，异或门的实现其实就是一个三层的神经网络。
  我们也得到一个概念：叠加了多层的感知机称为多层感知机，也可以叫做神经网络。
  所以，单层感知机只能表示线性空间，多层感知机可以表示非线性空间；多层感知机（理论上）也可以表示计算机。

总结

  修仙记录第一刻。（练气）
ps：1.作品一旦产生作家就已经死了，互相探讨，笔者还在学习中，有错误会及时改正。
  2.本节参考于斋藤康毅的两部作品。
  持续更新中~~~♪（＾∀＾●）ﾉｼ （●´∀｀）♪