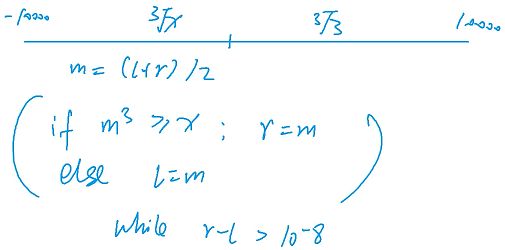习题 --- 快排、归并、浮点数二分

第 k 个数

给定一个长度是 n 的整数数列，以及一个整数 k，要求用快速选择算法求出数列的第 k 小的数是多少？

输入样例，表示一共有 5 个数，求第 3 小的数，数列为 2、4、1、5、3，也就是 1、2、3、4、5，第 3 小的数是 3，答案是 3

这道题目如果用快排来做，首先需要先把所有数排序，如果排序的话，时间复杂度就是 O(nlogn)，采用快选的原因就是它的时间复杂度比较低，时间复杂度为 O(n)

首先回忆一下快排 快排、归并、浮点数二分、高精度加、减法

以上就是快排的三个步骤，需要求从 l 到 r 这个区间里面第 k 小的数，快排的前两步会把整个区间划分成左右两段，由于左边所有数都是严格 ≤ 右边所有数，因此左边这半段里的所有数就是整个区间最小的那些数，可以统计左边这些数一共有多少个，假设左边所有数的个数为 SL，右边所有数的个数为 SR

分情况讨论

看 k 和 SL 的关系：如果 k ≤ SL，k ≤ 左半边区间数的个数，左边的数一定 ≤ 右边所有的数，整个区间第 k 小的数一定在左半边区间，因此只需要递归处理左边，k 一定不会在右边

第二种情况，k ＞ SL，k 大于左边数的个数，第 k 小的数一定在右半边，只需要递归处理右边

注意

k 表示整个区间第 k 小的数，左半边一共有 SL 个数比 k 小，所以整个区间第 k 小的数应该是右半边区间第 k - SL 小的数

快排需要递归左边、递归右边，快选每次不需要递归两边，只要选择一边递归就可以了

时间复杂度分析

第一层整个区间长度是 n，需要处理 0 ~ n - 1，第一层区间处理需要 O(n) 的时间，计算量是 n，第二层会递归到左边或者递归到右边，区间长度期望会缩小一半，第二层需要处理的区间长度变成 n / 2，同理第三层会把第二层的区间长度再除以 2，变成 n / 4，整理得，快速选择算法的时间复杂度为 O(2n)，也就是 O(n)

注意

在 c++ 中，如果局部变量和全局变量重名，优先使用局部变量

处理边界，如果 l 等于 r 说明区间里面只有一个数，返回当前这个数。递归的时候与二分类似，时时刻刻保证第 k 小的数在区间 [l，r] 里面，时时刻刻保证了区间里面至少有一个数，所以判断条件既可以是等于或者大于等于。当区间长度是 1 的时候，并且答案是在区间里面，那么这个数就一定是答案

#include 
#include 

using namespace std;

const int N = 100010;

//n表示所有数的个数 k表示第k小的数 
int n,k;
//存储所有数 
int q[N];
//lr表示区间左右端点 k表示第k小的数 
int quick_sort(int l,int r,int k)
{
	//处理边界
	if(l == r/* >=r 时刻保证第k小的数一定是在区间中 时刻保证区间中至少有一个数 快排区间中可能没有数可能会出现l>r的情况*/) return q[l];
	int x = q[l],i = l - 1,j = r + 1;
	while(i < j)
	{
		while(q[++i] < x);
		while(q[--j] > x);
		if(i < j) swap(q[i], q[j]);
	}
	//sl表示左半边区间中有多少个数,左半边区间的右边界是j-> 从l到j一共有多少个数? 
	int sl = j - l + 1;
	//如果k <= sl递归到左边 
	if(k <= sl) return quick_sort(l, j, k);
	//否则递归到右边 k变成k-sl
	return quick_sort(j + 1, r, k - sl);
}
int main()
{
    //读入每个数
	cin >> n >> k;
	for(int i = 0;i < n;i++ ) cin >> q[i];
	//传入一个k 直接返回第k小的数 
	cout << quick_sort(0, n - 1, k) << endl;
	return 0;
}

逆序对的数量

逆序对是一个数对，例如 5 2 2 1 4

从这个数对里面选两个数，满足前面一个的数比后面一个数大，就被称为逆序对，第一个 5 和第二个 2 就是一个逆序对，因为前面一个比后面一个大，同样第一个 5 和第三个 2 也是一个逆序对，. . . 以此类推，5 和 2、4、1 都满足逆序对，4 和 1 不满足逆序对，2 和 2 不满足逆序对【由于两个数相等，所以不满足逆序对，只有前一个数比后面一个数大才满足逆序对】

可以用分治的思路，回顾一下归并排序的过程 快排、归并、浮点数二分、高精度加、减法

第一步把整个区间一分为二，第二步递归排序两个子区间，第三步归并：将左右两个有序的序列合并成一个有序的序列

以上就是归并排序的基本流程，接下来看一下如何用归并排序去求逆序对

首先基于分治的思想，将所有的逆序对分成三大类：

①两个数同时出现在左半边

②两个数同时出现在右半边

③一个数在左半边，一个数在右半边

假定归并排序的函数可以把整个区间排好序，并且同时可以返回整个区间内部所有逆序对的个数

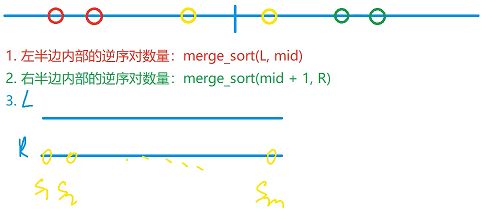
分三种情况来看，整个区间所有逆序对的个数应该是这三类之和，第一种是红色的情况，也就是全部在左半边的情况；第二种情况是绿色的情况，也就是全部在右半边的情况，关键是第三种逆序对的个数，左边这个数在左半边，右边这个数在右半边，假设左半边和右半边都已经排好序了，接下来考虑如何统计这样的情况？

假设左半边和右半边都已经排好序了，如何去统计黄色数对的个数呢？对于第二个序列的第一个数，我们可以先求在 L 里面有多少个数大于它，假设有 s1 个数大于这个数，那么和黄色这个点能构成逆序对的，并且另外在上面一个序列里面的这样的数对的个数是 s1，再看第二个点，看 L 这个序列里面有多少个数比第二个数大，假设为 s2，那么和这个点构成的逆序对的数量就是 s2，. . . 以此类推，一共有 m 个点，统计一下在 L 里面有多少个数比最后一个点要大，假设是 sm，说明第一个序列里面和这个点能构成逆序对的数的数量就是 sm，总共的黄色的逆序对的数量就是 s1 + . . . + sm，接下来看一下如何快速地计算出 s1 ~ sm？

这里就需要回顾一下归并排序的第三步，归并的过程：在归并的时候，其实用了两个指针来做，上面这个序列里面有一个红色指针，下面这个序列里面有一个绿色指针，都是从前往后指，每次选择把两个序列里面较小的那个数拿出来当作整个序列的当前最小的数。当绿色指针比红色指针要小的时候，即 qi ＞ qj 的时候，可以发现从 i 开始一直到最后，这个区间里面的所有数就是比 qj 大的所有上的数

首先从 qi 开始，后面的数都大于等于 qi，qi 之后的数都是严格大于 qj，那么 qi 之前的数是不是一定小于等于 qj 呢？

这是一定的，因为 qi 之前的数如果不小于等于 qj 的话就不会放到 tmp 数组中，这样红色的部分就不用考虑了，同理，绿色的部分也是如此，求逆序对的数量其实就是求黄色数对的数量

总结

qi 之前的数都是小于等于 qj，qi 后面的数都大于 qj，此时从 i 开始到最后，区间里面所有的数就是全部比 qj 大的数了，那么就可以求出来 sj 了，sj 就等于从 i 开始到上面区间最后一个数的个数，上面区间的左端点是 l，右端点是 mid，因此 sj = mid - l + 1，求黄色的数对的个数其实就是归并的过程，当我们要把 qj 输出出来的时候，就在答案里面加上 mid - l + 1 就可以了

数据范围为 10w，逆序对的数量最多是多少呢？首先，当我们整个序列是倒序的时候，逆序对的数量是最多的，n、n - 1、n - 2、. . . 1，n 与后面所有数都构成逆序对数量为 n - 1，n - 1 与后面所有的数都构成逆序对数量为 n - 2，一直加到 1，总共的数量为 n × (n - 1) / 2，也就是 5 × ，大于 int 的最大值，需要用 long long 存储

加号的优先级比右移运算符的优先级高，右移 1 等价于整除以 2，define 是宏定义，typedef 就是类型的宏定义

扫尾的时候虽然写了两重循环，但是这两重循环一定最多只会执行一个

#include 
#include 

using namespace std;

typedef long long LL;

const int N = 100010;

int n;
int q[N];
//归并排序需要一个临时数组存储中间排序的结果
int tmp[N];

LL merge_sort(int l, int r)
{
    if(l >= r) return 0;
    //取中间值
    int mid = l + r >> 1;
    LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);
    //归并过程
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
        if(q[i] <= q[j]) tmp[k++ ] = q[i++ ];
        //sj = mid - i + 1
        else     
        {
            tmp[k++ ] = q[j++ ];
            res += mid - i + 1;
        }
    //注意扫尾的时候不需要加上 由于一边已经扫完了 需要两个数对才能构成逆序对 '一个巴掌拍不响'
    while(i <= mid) tmp[k++ ] = q[i++ ];
    while(j <= r)   tmp[k++ ] = q[j++ ];
    //把临时数组排好序的结果放回原数组 i循环原数组 j循环临时数组
    for(i = l,j = 0;i <= r;i++, j++ ) q[i] = tmp[j];
    
    return res;
}

int main()
{
    cin >> n;
    for(int i = 0; i < n;i++ ) cin >> q[i];

    //merge_sort可以返回区间l到r里面所有逆序对的数量
    cout << merge_sort(0, n - 1) << endl;

    return 0;
}

数的三次方根

二分的第一步是确定边界，n 的范围是 -1w ~ 1w，所以答案的范围就是 -1w ~ 1w，注意：如果求的是数的二次方根，假设输入一个数 x ＞ 0，在定义边界的时候，让 l 等于 0，r 等于 x，注意这个是有问题的，当 x ＜ 1 的时候，例如 x = 0.01，如果我们要是按照这种方式来二分的话，就会在 0 ~ 0.01 里面去找答案，但是 等于 0.1，不在这个区间里面，所以答案的范围一定不能取 0 ~ x，如果想精确一点的话可以取 max(1，x)，右边界不能小于 1

这道题目的 一定是在范围 -1w ~ 1w 之间，接下来就是二分的步骤了，二分的判断条件是什么呢？

假设 m 是当前的中间点 m = (l + r) / 2，如果 ≥ x，说明 一定在 m 的左半边，把整个区间更新成左边的子区间，把当前区间从 l 到 r 更新成从 l 到 mid 就可以了 。否则 ＜ x，说明 一定在右半边子区间里面，把当前区间从 l 到 r 更新成从 mid 到 r 就可以了

如果题目要求保留四位小数：1e-6  保留五位小数：1e-7 保留六位小数：1e-8

至少要比要求的有效位数多 2

#include 
#include 

using namespace std;

int main()
{
    double x;
    cin >> x;
    double l = -10000, r = 100000;
    while(r - l  > 1e-8)
    {
        double mid = (l + r) / 2;
        if(mid * mid * mid >= x) r = mid;
        else l = mid;
    }
    //默认保留6位小数
    printf("%lf\n", l);
    return 0;
}