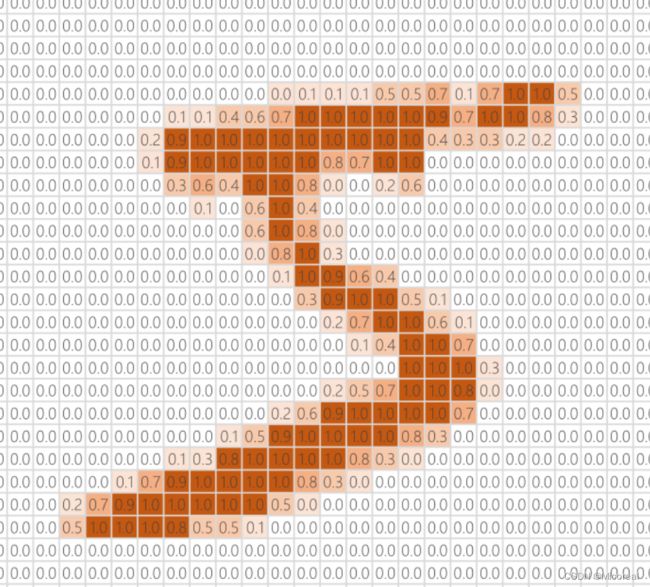9 多分类问题

课程内容来源： 链接
课程文本借鉴： 链接
以及Birandaの

突然发现的也挺好：链接

问题引入

前篇中，对糖尿病数据集的问题是一个二分类问题，但实际问题中，二分类问题较少，更多的是以MINIST、CIFAR为例的多分类问题。

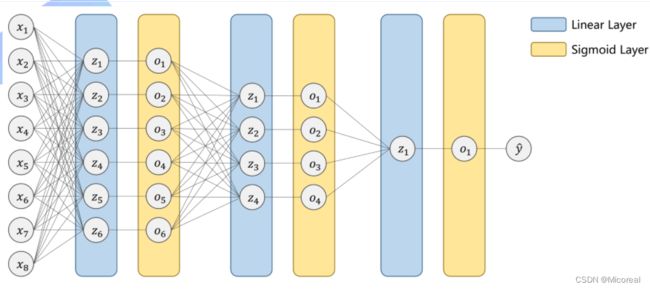
网络设计

把每一个分类作为二分类进行判断。

eg：当输出为1时，对其他的非1输出都规定为0，以此来进行判断。

但这种情况下，类别之间所存在的互相抑制的关系没有办法体现，当一个类别出现的概率较高时，其他类别出现的概率仍然有可能很高。
换言之，当计算输出为1的概率之后，再计算输出为2的概率时，并不是在输出为非1的条件下进行的，也就是说，所有输出的概率之和实际上是大于1的。
即对于一个多分类问题，其解决方案应该基于如下要求：

每个分类的出现概率大于等于0
$$P(y=i)\ge 0$$

各个分类出现概率之和为1
$$\sum _{i=0}^{n}P(y=i)=1$$
综上，多分类输出之间是需要有竞争性的

改进网络方法

改最后的sigmod层为softmax层，来实现多分类问题的基本要求。

softmax层

假定$Z^l$为最后一层线性层的输出,$Z_i$为第i类的输出。则最终的softmax层函数应为
$$P(y=i)=\frac{e^{z_i}}{{\sum }_{j=0}^{K-1}{e}^{z_i}},i\in \{0,\cdots ,K-1\}$$

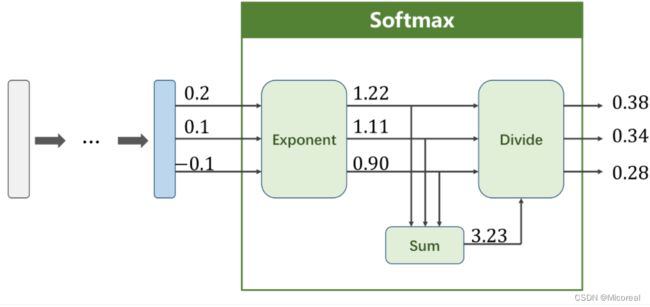
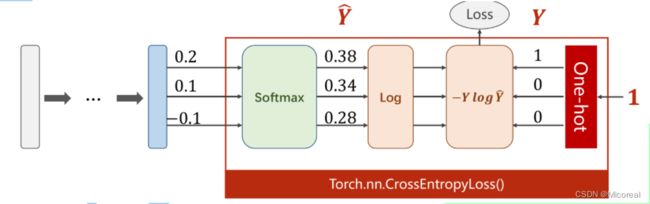
事实上，对于多分类问题输出，Softmax会先对所有输出进行指数运算，以满足（1）式要求，再对结果进行归一化处理，以满足（2）式要求。

loss

依照前篇所提及的交叉熵相关理论可知，交叉熵的计算公式如下
$$H(P,Q)=-\sum _{i=1}^{n}P(X_i)log(Q(X_i))$$
在多分类问题中，该公式可扩展为
$$H(P,Q)=-\sum _{i=1}^n\sum _{j=1}^{m}P(X_{ij})log(Q(X_{ij}))$$

由于上述计算过程中$P(X_{ij})$非0即1，且有且只能有一个1，因此一个样本所有分类的loss计算过程可以简化为
$$Loss=-log(P(X))=-YlogY$$
其中，$X$表示事件预测值与实际值相同，$Y$表示非0即1的指示变量，$Y$表示Softmax的输出。
此时$Y$其实是作为独热编码（One-hot）输入的，以对离散的变量进行分类。即只在实际值处为1，其他均为0.

MINIST引入

MINIST数据集中每个数字都是一个$28\ast 28=784$大小的灰度图，将灰度图中的每个像素值映射到$(0,1)$区间内，可以进行映射。

代码实现

包引入

import torch
#组建DataLoader
from torchvision import transforms #图像
from torchvision import datasets
from torch.utils.data import DataLoader
#激活函数和优化器
import torch.nn.functional as F
import torch.optim as optim

数据准备

#Dataset&Dataloader必备
bacth_size = 64
#pillow（PIL）读的原图像格式为W*H*C，原值较大
# 转为格式为C*W*H值为0-1的Tensor
transform = transforms.Compose([
    #变为格式为C*W*H的Tensor
    transforms.ToTensor(),
    #第一个是均值，第二个是标准差，变值为0-1
    transforms.Normalize((0.1307, ), (0.3081, ))
])

train_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=True,
                               download=True,
                               transform = transform)

train_loader = DataLoader(train_dataset,shuffle=True,batch_size=bacth_size)

test_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=False,
                               download=True,
                               transform = transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=bacth_size)

模型设计

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 线性层1，input784维 output512维
        self.l1 = torch.nn.Linear(784, 512)
        # 线性层2，input512维 output256维
        self.l2 = torch.nn.Linear(512, 256)
        # 线性层3，input256维 output128维
        self.l3 = torch.nn.Linear(256, 128)
        # 线性层4，input128维 output64维
        self.l4 = torch.nn.Linear(128, 64)
        # 线性层5，input64维 output10维
        self.l5 = torch.nn.Linear(64, 10)
    
    def forward(self, x):
        # 改变张量形状view\reshape
        # view 只能用于内存中连续存储的Tensor，transpose\permute之后的不能用
        # 变为二阶张量（矩阵），-1用于计算填充batch_size
        x = x.view(-1, 784)
        # relu 激活函数
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        # 第五层不再进行relu激活
        return self.l5(x)

model = Net()

Loss&Optimizer

#交叉熵损失
criterion = torch.nn.CrossEntropyLoss()
#随机梯度下降，momentum表冲量，在更新时一定程度上保留原方向
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

模型训练及测试

def train(epoch):
    running_loss = 0.0
    #提取数据
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        #优化器清零
        optimizer.zero_grad()
        #前馈+反馈+更新
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()
        #累计loss
        running_loss += loss.item()

        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
            running_loss = 0.0

def test():
    correct = 0
    total = 0
    #避免计算梯度
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            #取每一行（dim=1表第一个维度）最大值（max）的下标(predicted)及最大值(_)
            _, predicted = torch.max(outputs.data, dim=1)
            #加上这一个批量的总数（batch_size），label的形式为[N,1]
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
        print('Accuracy on test set: %d %%' % (100 * correct/total))
        
if __name__=='__main__':
    for epoch in range(10):
        train(epoch)
        test()