蓝桥杯：算法很美 笔记 3.查找和排序（Python实现）

1.分治法介绍以及关键点解析

• 分治法(divide and conquer, D&C)∶将原问题划分成若干个规模较小而结构与原问题一致的子问题﹔递归地解决这些子问题，然后再合并其结果，就得到原问题的解。

• 容易确定运行时间，是分治算法的优点之一。

• 分治模式在每一层递归上都有三个步骤一分解(Divide) :

• 将原问题分解成一系列子问题;

• 解决(Conquer):递归地解各子问题。若子问题足够小,则直接有解;

• 合并(Cpmbine);将子问题的结果合并成原问题的解。

分治法关键点

• 原问题可以一直分解为形式相同子问题，当子问题规模较小时，可自然求解，如一个元素本身有序

• 子问题的解通过合并可以得到原问题的解

• 子问题的分解以及解的合并—定是比较简单的，否则分解和合并所花的时间可能超出暴力解法，得不偿失

2.快速排序

快速排序算法：

1. 分解︰数组A[p..r]被划分为两子数组A[p..q-1]和A[ q+1,r]，使得A[q]为大小居中的数，左侧A[p..q-1]中的每个元素都小于等于它，而右侧A [ q+1,r]中的每个元素都大于等于它。其中计算下标q也是划分过程的一部分。

2. 解决:通过递归调用快速排序，对子数组A[p ..q-1]和A[ q+1,r]进行排序

3. 合并:因为子数组都是原址排序的，所以不需要合并，数组A[p..r]已经有序

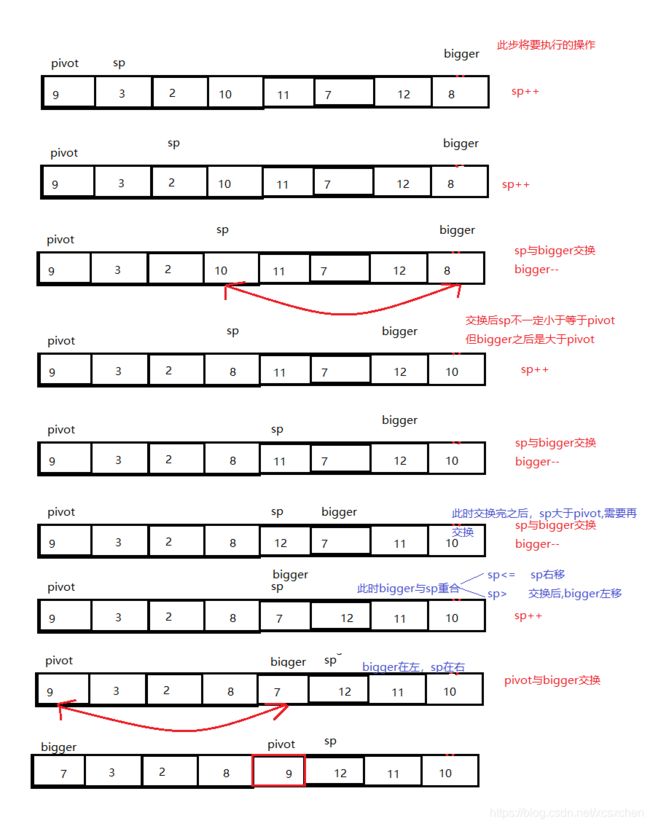
1. • 一遍单向扫描法:

• 一遍扫描法的思路是，用两个指针将数组划分为三个区间

• 扫描指针(scan_pos)左边是确认小于等于主元的

• 扫描指针到某个指针(next_bigger_pos)中间为未知的，因此我们将第二个指针(next_bigger_pos) 称为未知区间末指针，末指针的右边区间为确认大于主元的元素

伪码实现

QuickSort
    quickSort(A,p,r)
        if(p

nums = [5, 6, 4, 5, 3, 1, 8, 9, 7]
 
def QuickSort(num):
    # 若列表长度为1，直接输出不用排序  
    if len(num) <= 1:                        
        return num
    # 取数组的第一个数作为基值
    key = num[0]  
    # 定义空列表用来储存大于/小于/等于基准值的元素                          
    llist, mlist, rlist = [], [], []  
    # 定义空列表用来储存大于/小于/等于基准值的元素     
    for i in range(0, len(num)):            # 遍历列表，把元素归类到三个列表中
        if num[i] < key:
            llist.append(num[i])
        elif num[i] > key:
            rlist.append(num[i])
        else:
            mlist.append(num[i])
    # 对左右两个列表进行快排，拼接三个列表并返回
    return QuickSort(llist) + mlist + QuickSort(rlist)  
 
 
print(QuickSort(nums))

2. • 双向扫描法:

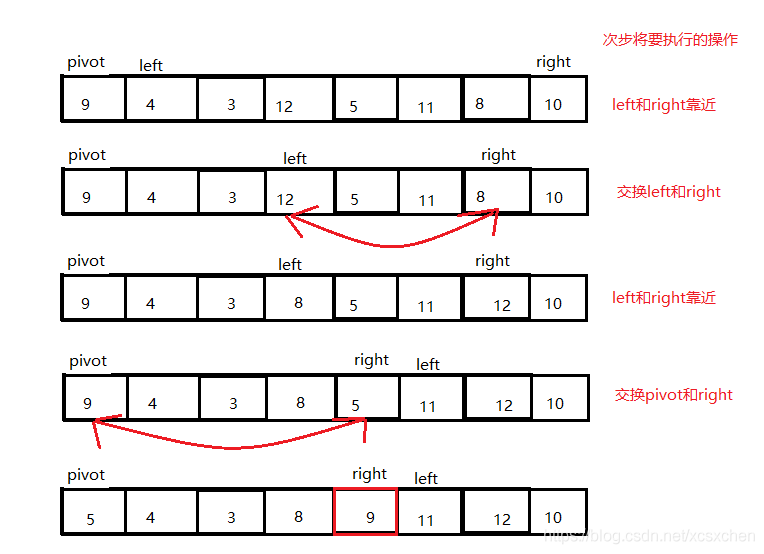
双向扫描的思路是,头尾指针往中间扫3描,从左找到大于主元的元素,从右找到小于等于主元的元素二者交换,继续扫描,直到左侧无大元素,右侧无小元素

QuickSort2
    pivot = A[p]
    left = p + 1 // 扫描指针
    right = r // 右侧指针
    while (left <= right):
        {  //left不停往右走，直到遇到大于主元的元素
        while(left <= right && A[left]<=pivot)left++;  //循环退出时，left一定是指向第一个大于主元的位置
        while(left <= right && A[right]>pivot)right--;   //循环退出时，right一定是指向最后一个小于等于主元的位置
        if(left <= right)
            swap(A,left,right);
        }
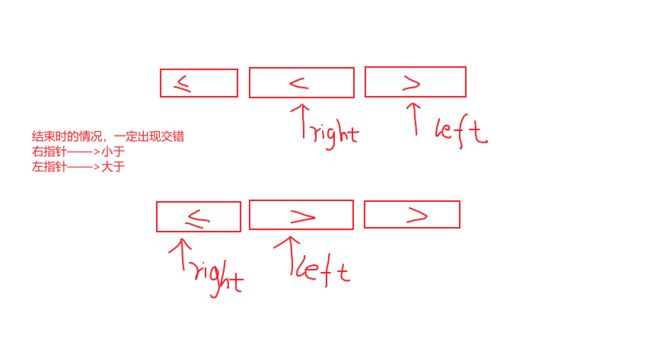
        // while退出时，两者交错，且right指向的是最后一个小于等于主元的位置，也就是主元应该呆的位置
        swap(A, p, right);
        return right;

# QSort
nus = [4, 5, 1, 2, 3, 5, 4, 1]
 
# left,right分别为子数组中第一个元素和最后一个元素在原数组中的位置
def QSort(left, right):
    # 边界条件               
    if left >= right:                
        return
    # 初始化左右指针的初始值
    l, r, key = left, right, nus[left] 
    # 调整元素的位置 
    while l < r:                     
        while l < r and nus[r] >= key:
            r -= 1
        nus[l] = nus[r]
        while l < r and nus[l] <= key:
            l += 1
        nus[r] = nus[l]
    # 把基准值赋给左右指针共同指向的位置
    nus[r] = key 
    # 对左侧数组排序                   
    QSort(left, l-1)  
    # 对右侧数组排序              
    QSort(l+1, right)               
QSort(0, len(nus) - 1)
print(nus)

3.工程实践中的其他优化

• 三点中值法

• 绝对中值法

• 待排序列表较短时,用插入排序 (n≤8)

3.归并排序

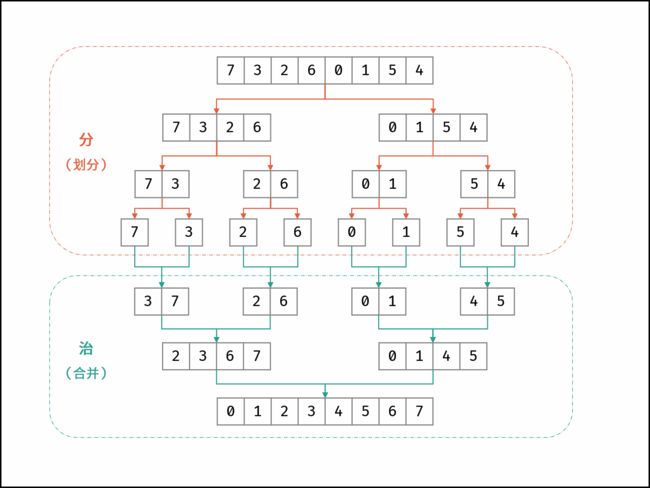
• 归并排序(Merge Sort)算法完全依照了分治模式

• 分解:将n个元素分成各含n/2个元素的子序列;

• 解决:对两个子序列递归地排序;

• 合并:合并两个已排序的子序列以得到排序结果

• 和快排不同的是

• 归并的分解较为随意

• 重点是合并、

归并过程分析

'''归并排序'''

def merge_sort(arr, left, right):
    if left == right:
        return
    mid = left + ((right - left) >> 1)
    merge_sort(arr, left, mid)
    merge_sort(arr, mid + 1, right)
    merge(arr, left, mid, right)


def merge(arr, left, mid, right):
    help = []
    p1 = left
    p2 = mid + 1
    while p1 <= mid and p2 <= right:
        if arr[p1] <= arr[p2]:
            help.append(arr[p1])
            p1 += 1
        else:
            help.append(arr[p2])
            p2 += 1
    while p1 <= mid:
        help.append(arr[p1])
        p1 += 1
    while p2 <= right:
        help.append(arr[p2])
        p2 += 1
    arr[left:right + 1] = help

ls = [7, 3, 2, 6, 0 , 1 , 5 , 4]
merge_sort(ls, 0, len(ls) - 1)
print(ls)

4.解题

题1:调整数组顺序使奇数位于偶数前面

1.新建一个整数数组，利用二分思想，遍历原数组，遇到奇数从首天剑，偶数从尾部添加，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。要求时间复杂度为O(n)。

2.快排思想，左指针位于首元素，右指针位于末元素，找到第一个奇，偶就对调位置，不需要额外空间。

3.遍历，依次寻找奇偶元素

def exchange(nums):
        low=0
        high=len(nums)-1

        while low

class Solution:

    def fun1(self, array):
        """奇数在前，偶数在后，相对位置保持不变"""
        new_arry = []

        for i in range(len(array)):
            if array[i] & 1 == 1:  # 二进制与操作，奇数（***1(奇数) & 0001 = 0001）
                new_arry.append(array[i])
        for j in range(len(array)):
            if array[j] & 1 == 0:
                new_arry.append(array[j])

        return new_arry

    def fun2(self, array):

        # sorted 默认降序排列
        return sorted(array, key=lambda x: x % 2, reverse=True)

    def fun3(self, array):
        """冒泡排序"""

        for i in range(len(array) - 1):
            flag = False
            for j in range(len(array) - 1 - i):
                if array[j] % 2 == 0 and array[j + 1] % 2 == 1:
                    # change position
                    array[j], array[j + 1] = array[j + 1], array[j]
                    flag = True
            if flag is False:
                break
        return array

        return array

题2:第k个元素

以尽量高的效率求出一个乱序数组中按数值顺序的第K个元素值

利用快速排序的分区思想，执行完partition之后，左边元素小于q，右边大于q，q的位置为实际排序后的位置，如果它的序列为k，则p为所求元素，大于k，继续在左半部分查找，小于k，在右半部分查找

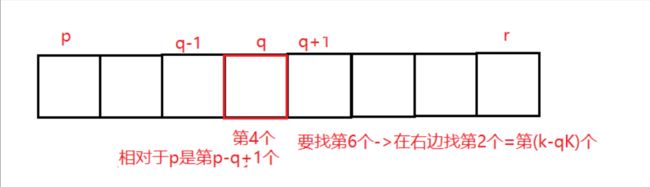
def selectK(A, p, r, k):# k为要找第k个
        q=QSort(A,p,r)
        qK=q-p+1   # 在p~r中第几个
        if(k==qK):
            return A[q]
        elif(k

输入n个整数，找出其中最小的K个数。

class Solution:
    def GetLeastNumbers_Solution(self, a, k):
        def partition(a, low, high):
            pivot = a[low] #枢轴为第一个元素
            while low < high:
                #从右向左找比枢轴元素小的数，移到左边（枢轴整好空一个位置出来，所以放到左边）
                while low < high and a[high] >= pivot:
                    high -= 1
                a[low] = a[high]

                #从左向右找比枢轴大的数，移到右边的空位上（上一步右边一个数移到左边，空出一个位置）
                while low < high and a[low] <= pivot:
                    low += 1
                a[high] = a[low]

            a[low] = pivot #最后low=high，枢轴就在这个位置
            return low #返回枢轴位置
        
        def find_k_small(a, low, high):
            pos = k-1
            if low < high:
                index = partition(a, low, high)
                
                if index < pos:
                    index = find_k_small(a, index+1, high)
                if index > pos:
                    index = find_k_small(a, low, index)
                return index
        
        if len(a) < k:
            return []
        if k-1 < 0:
            return []
        if k == len(a):
            a.sort()
            return a
        index = find_k_small(a, 0, len(a)-1)
        sub = a[:index+1]
        sub.sort()
        return sub

题3:超过一半的数字

数组中有一个数字出现的次数超过了数组长度的一半，找出这个数字。

def over_half_list(list):
    # 数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字
    len_list = len(list)
    dict = {}
    #转字典，方遍统计字数
    for i in list:
        dict[i] = list.count(i)
    #判断哪个key的value>len_list/2
    for k,v in dict.items():
        if v > len_list/2:
            print('所得到的数字是：%d，他的次数是%d，数组长度是%d'%(k,v,len_list))

list = [2,3,4,56,7,4,4,5,4,4,3,4,4,23,4,2,4,4]
over_half_list(list)-

方法二：

'''
>该题目就是要找到数组中的超过一半的数字
>其实有一种最简单得方法就是将数组进行排序
>数组中间的值一定是超过一半的数字
>还有一种方法就是摩尔选票，什么意思？
>就是一种不断抵消选票的原理
>先假设第一个是最终的结果，
>遍历第二个元素时，如果与第一个相同就将选票+1
>否则将第一个人的选票抵消
>最终有票数的就是最多的人

'''
class Solution:
    def majorityElement(self, nums):
        res = 0
        tickets = 0

        for num in nums:
            if tickets == 0:
                res = num
            if num == res:
                tickets += 1
            else:
                tickets -= 1

        return res
nums=[1,2,3,4,5,7,7,7,7,7,7]
a=Solution()
print(a.majorityElement(nums))

题3扩展:寻找发帖“水王”

Tango是微软亚洲研究院的-一个试验项目。研究院的员工和实习生们都很喜欢在Tango上面交流灌水。传说，Tango 有一大“水王”，他不但喜欢发贴，还会回复其他ID发的每个帖子。**坊间风闻该“水王”发帖数目超过了帖子总数的一半。**如果你有一个当前论坛上所有帖子(包括回帖)的列表，其中帖子作者的ID也在表中，你能快速找出这个传说中的Tango水王吗?

与题三解法相同

水王增强

出现次数恰好为个数的一半，求出这个数

'''
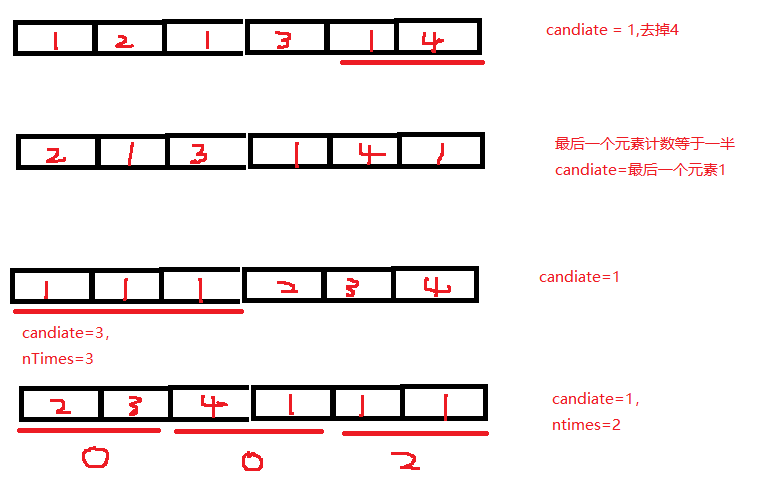
  水王占总数的一半，说明总数必为偶数；
  不失一般性，假设隔一个数就是水王的id，两两不同最后一定会消减为0
  水王可能是最后一个元素，每次扫描的时候，多一个动作，和最后一个元素做比较，单独计数，计数恰好等于一半
  如果不是，计数不足一半，那么去掉最后一个元素，水王就是留下的那个candidate
'''
def  solution(arr):
    candidate = arr[0]
    nTimes = 0
    countOfLast = 0 #统计最后这个元素出现的次数
    N = len(arr)
    i=0
    while(i

题4:最小可用ID

在非负数组(乱序)中找到最小的可分配的id (从1开始编号),数据量1000000

# O(N²) 暴力解法:从1开始依次探测每个自然数是否在数组中
def find1(arr):
  i = 1
  while (i<=len(arr)):  # [1,2,3] len=3
    if (i not in arr):
      return i
    i+=1
  return i



# NlogN
def find2(arr):
  arr.sort()  # NlogN  先排序
  i = 0;
  while (i < len(arr)):   # [1,2,3]
    if (i + 1 != arr[i]):   # 不在位的最小的自然数
      return i + 1;
    i+=1
  return i + 1;

''''**
 * 改进1：
 * 用辅助数组
 * 遍历数组,如果对应值有，将辅助数组的值赋值为1，大于数组长度的值可以不管
 * 查找辅助数组，返回第一个0值
 '''
def find3(arr):
  n = len(arr)
  helper =[0 for i in range(n+1)]
  i=0
  while(i r):
#     return l + 1
#   midIndex = l + ((r - l) >> 1)  #中间下标
#   q = Qsort(arr, l, r, midIndex - l + 1)  #实际在中间位置的值
#   t = midIndex + 1  #期望值
#   if (q == t):  #左侧紧密
#     return find4(arr, midIndex + 1, r)
#   else:   #左侧稀疏
#     return find4(arr, l, midIndex - 1)
  

arr=[1,2,3]
print(find1(arr))
print(find2(arr))
print(find3(arr))

题5:合并有序数组

给定两个排序后的数组A和B，其中A的末端有足够的缓冲空间容纳B。编写一个方法，将B合并入A并排序

一种简易方法：用arr2直接覆盖arr1中的0元素，然后进行排序

class Solution:
    def merge(self, nums1, m, nums2, n):
        p1 = m - 1   # 两个数组指针都指向尾部
        p2 = n - 1
        p = m + n - 1   # 计算合并后总长度，尾指针指向位置，总共有3个指针
        while p1 >= 0 and p2 >= 0:
            if nums1[p1] < nums2[p2]:
                nums1[p] = nums2[p2]
                p2 -= 1
            else:
                nums1[p] = nums1[p1]
                p1 -= 1
            p -= 1
        nums1[:p2+1] = nums2[:p2+1]   
        # P1为空，直接将P2剩下的粘过去
        # P2为空，不进行操作，P1元素不动
a=Solution()
arr1=[1,2,2,3,7,0,0,0]
arr2=[3,4,5]
a.merge(arr1,5,arr2,3)
print(arr1)

题6:逆序对个数

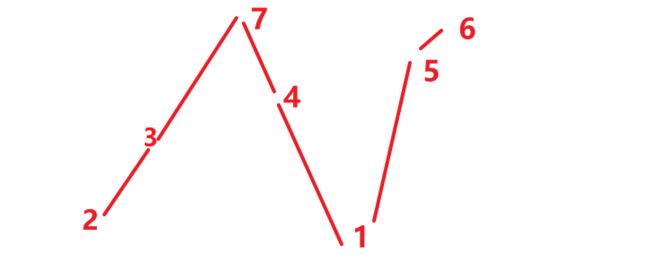
一个数列，如果左边的数大，右边的数小，则称这两个数位一个逆序对。求出一个数列中有多少个逆序对。例如 5 2 就是一个逆序对

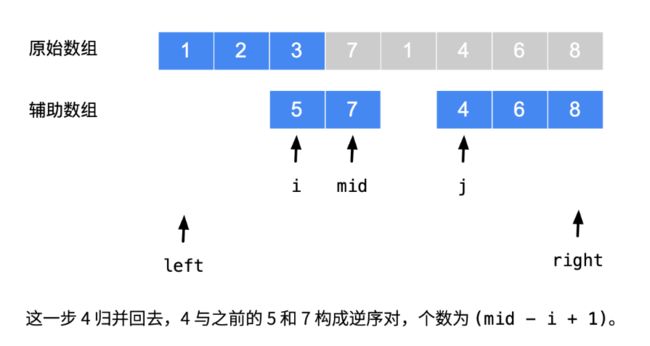
解题思路为二分归并排序，如果选左边第一个，说明左边第一个比右边第一个小，所以左边第一个比右半部都小，类似，如果选右边第一个，说明右边第一个比左边第一个小，所以右边第一个比左半部都小，此时产生逆序对，个数为左边剩余全部的个数 ，即mid - left + 1 [1,2,3,4,5] 个数为5-1+1=5

方法一：暴力

# -*- coding:utf-8 -*-
class Solution:
    def InversePairs(self, data):
        # write code here
        # 思路一：暴力解，两个循环
        # 运行超时，暴力解不行哦
        length = len(data)
        if(length == 0):
            return 0
        else:
            num = 0
            for i in range(length-1):
                point = data[i]
                for j in range(i,length):
                    if(data[i]>data[j]):
                        num += 1
            return num
a=Solution()
data=[5,3,2,1]
print(a.InversePairs(data))

方法二：二分归并

# -*- coding:utf-8 -*-
class Solution:
    def InversePairs(self, data):
        # write code here
        num, new_list = self.mergeSort(data)
        return num%1000000007

    def mergeSort(self, data):
        # 逆序对个数
        InversePairsNum = 0
        # 归并过程
        def merge(left,right):
            # 合并时发现的逆序对个数
            InversePairsNum = 0
            result = [] # 保存归并后的结果
            i = j = 0
            while(i

5.树、二叉树介绍

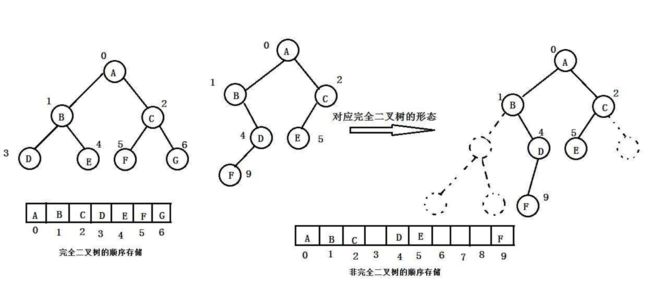
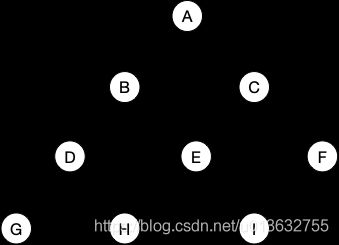
1.用数组表示二叉树：

根结点为0

左儿子 2i+1

右儿子 2i+2

父节点(i-1)/2

2.三种遍历方式

1.先序遍历（根左右）

若二叉树为空，则空操作；否则：

（1）访问根结点

（2）先序遍历左子树

（3）先序遍历右子树

2.中序遍历（左根右）

若二叉树为空，则空操作；否则：

（1）中序遍历左子树

（2）访问根结点

（3）中序遍历右子树

3.后序遍历（左右根）

若二叉树为空，则空操作；否则：

（1）后序遍历左子树

（2）后序遍历右子树

（3）访问根结点

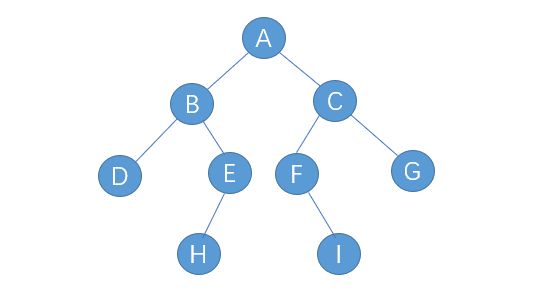
先序：ABDEHCFIG

中序：DBHEAFICG

后序：DHEBIFGCA

class TreeNode:

    def __init__(self, data) -> None:
        self.data = data  # 数据
        self.left = None  # 左子节点
        self.right = None  # 右子节点


def fixed_tree():
    """
    返回固定二叉树结构
    :return:
    """
    a = TreeNode('A')
    b = TreeNode('B')
    c = TreeNode('C')
    d = TreeNode('D')
    e = TreeNode('E')
    f = TreeNode('F')
    g = TreeNode('G')
    h = TreeNode('H')
    i = TreeNode('I')
    a.left = b
    a.right = c
    b.left = d
    c.left = e
    c.right = f
    d.left = g
    d.right = h
    e.right = i
    return a


def pre_order_traverse(_binary_tree):
    """
    前序遍历
    :param _binary_tree: 二叉树
    :type _binary_tree: TreeNode
    """
    if _binary_tree is None:
        return
    print(_binary_tree.data, end=',')
    pre_order_traverse(_binary_tree.left)
    pre_order_traverse(_binary_tree.right)


def in_order_traverse(_binary_tree):
    """
    中序遍历
    :param _binary_tree: 二叉树
    :type _binary_tree: TreeNode
    """
    if _binary_tree is None:
        return
    in_order_traverse(_binary_tree.left)
    print(_binary_tree.data, end=',')
    in_order_traverse(_binary_tree.right)


def post_order_traverse(_binary_tree):
    """
    后序遍历
    :param _binary_tree: 二叉树
    :type _binary_tree: TreeNode
    """
    if _binary_tree is None:
        return
    post_order_traverse(_binary_tree.left)
    post_order_traverse(_binary_tree.right)
    print(_binary_tree.data, end=',')


def layer_order_traverse(_layer_nodes):
    """
    按层遍历
    :param _layer_nodes: 当前层节点集合
    :type _layer_nodes: list
    """
    if _layer_nodes is None or len(_layer_nodes) == 0:
        return
    _childs = []  # 子集
    for _node in _layer_nodes:  # 遍历传入的当前层所有节点
        print(_node.data, end=',')
        if _node.left:
            _childs.append(_node.left)
        if _node.right:
            _childs.append(_node.right)
    layer_order_traverse(_childs)


if __name__ == '__main__':
    binary_tree = fixed_tree()
    print('前序遍历：', end='')
    pre_order_traverse(binary_tree)
    print()
    print('中序遍历：', end='')
    in_order_traverse(binary_tree)
    print()
    print('后序遍历：', end='')
    post_order_traverse(binary_tree)
    print()
    print('按层遍历：', end='')
    layer_order_traverse([binary_tree])
    print('\b' * 1, end='')

3.堆的概念

• 二叉堆是完全二叉树或者是近似完全二叉树。

• 二叉堆满足二个特性:
  1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
  2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。

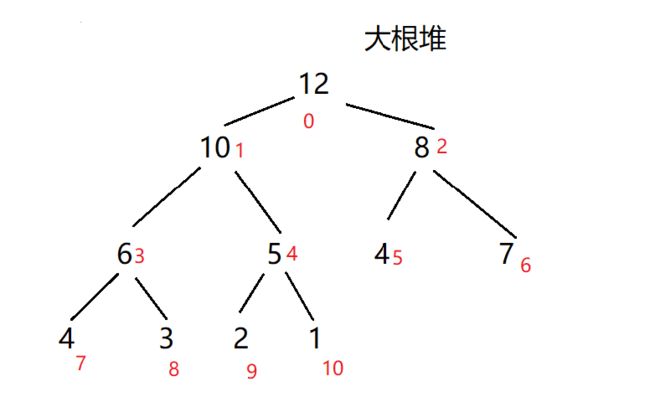
• 任意节点的值都大于其子节点的值—大顶堆

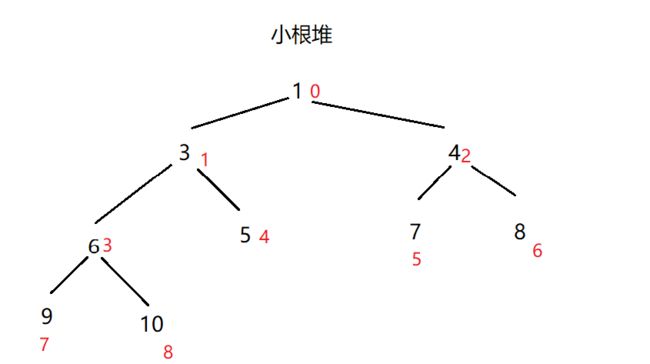
• 任意节点的值都小于其子节点的值—小顶堆

6.堆排序

排序思想

1.首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

注意:升序用大根堆，降序就用小根堆(默认为升序)

通过该步骤得到从大到小的排序顺序

7.计数排序

用辅助数组对数组中出现的数字计数,元素转下标,下标转元素

思路：开辟新的空间，空间大小为max(source)扫描source，将value作为辅助空间的下标，用辅助空间的改位置元素记录value的个数如：9 7 5 3 1 ，helper=arr(10)一次扫描，value为9，helper[9]++，value为7，将helper[7]++……如此这般之后，我们遍历helper，如果该位（index）的值为0，说明index不曾在source中出现如果该位（index)的值为1，说明index在source中出现了1次，为2自然是出现了2次，遍历helper就能将source修复为升序排列

时间复杂度： 扫描一次source，扫描一次helper，复杂度为N+k

空间复杂度：辅助空间k，k=maxOf(source)

计数有缺陷，数据较为密集或范围较小时，适用。

static void CountSort(int[] a) {
    int max = a[0];
    for (int e : a) {
        if (e > max) {
            max = e;
        }
    }
    int[] helper = new int[max + 1];
    for (int e : a) {
        helper[e]++;
    }
    int current = 0;//数据回填的位置
    for (int i = 1; i < helper.length; i++) {
        while (helper[i] > 0) {
            a[current++] = i;
            helper[i]--;
        }
    }
}

8、桶排序

• 一句话:通过"分配”和"收集”过程来实现排序

• 思想是:设计k个桶( bucket) ( 编号0~k-1 ) ,然后将n个输入数分布到各个桶中去,对各个桶中的数进行排序,然后按照次序把各个桶中的元素列出来即可。

• 计数是不是有点桶的味道?

• 由于实现需要链表,我们再讲到链表的时候再回来写这个代码

类似计数排序（一个数一个桶），桶排序（多个数一个桶），桶内要有序，再依次遍历桶

9、基数排序

思路：是一种特殊的桶排序

(1)假设有欲排数据序列如下所示:

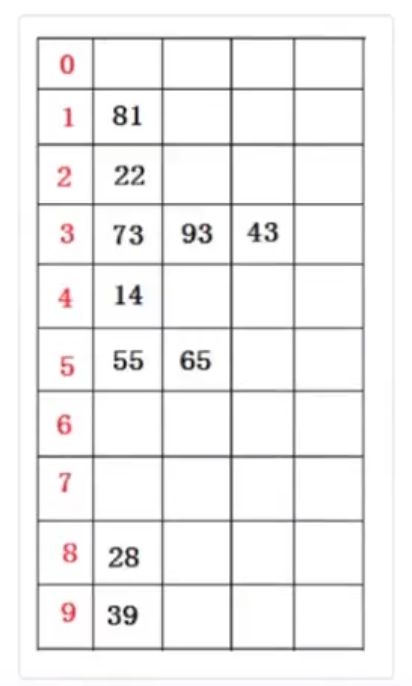
77 22 93 43 55 14 28 65 39 81

首先根据个位数的数值，在遍历数据时将它们各自分配到编号0至9的桶（个位数值与桶号一―对应)中。

81 22 73 93 43 14 55 65 28 39

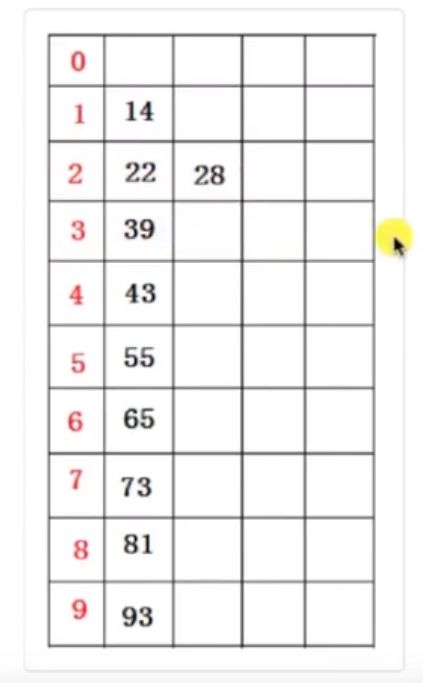
(2)接着，再进行一次分配，这次根据十位数值来分配（原理同上)，分配结果(逻辑想象）如下图

所示:

14 22 28 39 43 55 65 73 81 93

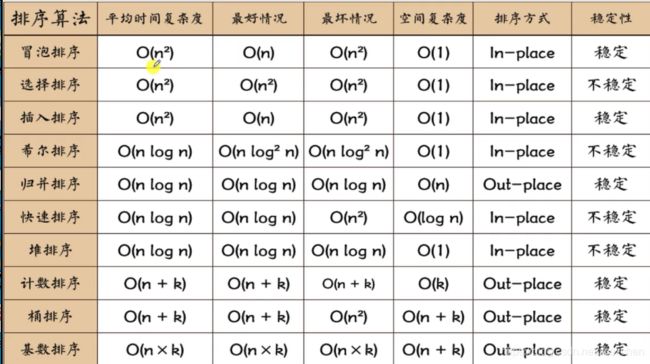
排序算法的总结：

#基础排序

a.冒泡

谁大谁上，每一轮都把最大的顶到天花板

效率太低O(n²)——掌握swap

b.选择排序，效率较低，但经常用它内部的循环方式来找最大值和最小值——怎么一次性求出数组的最大值和最小值

O(n²)

c.插排，虽然平均效率低，但是在序列基本有序时，它很快，所以也有其适用范围

Arrays这个工具类在1.7里面做了较大改动

d.希尔（缩小增量排序），是插排的改良，对空间思维训练有帮助

#分治法

1.子问题拆分

2.递归求解子问题

3.合并子问题的解

e.快排是软件工业中最常见的常规排序法，其双向指针扫描和分区算法是核心，

往往用于解决类似问题，特别地partition算法用来划分不同性质的元素，

partition->selectK,也用于著名的top问题

O(NlgN)，但是如果主元不是中位数的话，特别地如果每次主元都在数组区间的一侧，复杂度将退化为N²

工业优化：三点取中法，绝对中值法，小数据量用插入排序

快排重视子问题拆分

f.归并排序，空间换时间——逆序对数

归并重视子问题的解的合并

g.堆排序，用到了二叉堆数据结构，是继续掌握树结构的起手式

=插排+二分查找

上面三个都是NlgN的复杂度，其中快排表现最好，是原址的不用开辟辅助空间；堆排也是原址的，但是常数因子较大，不具备优势。

上面7种都是基于比较的排序，可证明它们在元素随机顺序情况下最好是NlgN的，用决策树证明

---

---

下面三个是非比较排序，在特定情况下会比基于比较的排序要快：

1.计数排序，可以说是最快的：O(N+k),k=maxOf(sourceArr)，

用它来解决问题时必须注意如果序列中的值分布非常广（最大值很大，元素分布很稀疏），空间将会浪费很多

所以计数排序的适用范围是：序列的关键字比较集中，已知边界，且边界较小

2.桶排序：先分桶，再用其他排序方法对桶内元素排序，按桶的编号依次检出。（分配-收集）

用它解决问题必须注意序列的值是否均匀地分布在桶中。

如果不均匀，那么个别桶中的元素会远多于其他桶，桶内排序用比较排序，极端情况下，全部元素在一个桶内

还是会退化成NlgN

其时间复杂度是：时间复杂度： O(N+C)，其中C=N*(logN-logM)，约等于N*lgN

N是元素个数，M是桶的个数。

3.基数排序，kN级别（k是最大数的位数）是整数数值型排序里面又快又稳的，无论元素分布如何，

只开辟固定的辅助空间（10个桶）

对比桶排序，基数排序每次需要的桶的数量并不多。而且基数排序几乎不需要任何“比较”操作，而桶排序在桶相对较少的情况下，

桶内多个数据必须进行基于比较操作的排序。

因此，在实际应用中，对十进制整数来说，基数排序更好用。

期望水准：

1、准确描述算法过程

2、写出伪代码

3、能分析时间复杂度

4、能灵活应用（知道优缺点和应用场景）

在查找算法中，基于比较的查找算法最好的时间复杂度也是O(logN)。

比如折半查找、平衡二叉树、红黑树等。

但是Hash表却有O©线性级别的查找效率(不冲突情况下查找效率达到O(1))。

大家好好体会一下：Hash表的思想和桶排序是不是有异曲同工之妙呢?

排序算法可视化网站 Data Structure Visualization (usfca.edu)

题7 :排序数组中找和的因子

• 给定已排序数组arr和k ,不重复打印arr中所有相加和为k的不降序二元组

• 如输入arr={-8,-4,-3,0,2,4,5,8,9,10},k=10

• 输出(0,10)(2,8)

1.左右两个指针，首尾相加，如果小于10，左指针右移动，大于10，右指针左移动。

2.遍历，二分法查找加起来等于10的元素。

• 扩展:三元组呢?

题8:需要排序的子数组

给定一个整数数组，你需要寻找一个连续的子数组，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

你找到的子数组应是最短的，请输出它的长度。

示例 1:

输入: [2, 6, 4, 8, 10, 9, 15]

输出: 5

解释: 你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

说明 :

输入的数组长度范围在 [1, 10,000]。

输入的数组可能包含重复元素 ，所以升序的意思是<=。

##

//扩展右端点：更新历史最高，只要右侧出现比历史最高低的，就应该将有边界扩展到此处

//找左端点：更新历史最低，只要左侧出现比历史最低高的，就应该将左边界扩展到此处

题9 :前k个数

• 求海量数据（正整数）按逆序排列的前k个数（topK），因为数据量太大，不能全部存储在内存中，只能一个一个地从磁盘或者网络上读取数据，请设计一个高效的算法来解决这个问题。 第一行用户输入K，代表要求得topK 随后的N（不限制）行，每一行是一个整数代表用户输入的数据，直到用户输入-1代表输入终止，请输出topK，空格分割。

• **思路：**先开辟一个K大小的数组arr，然后读取K个数据存储到数组arr，读到K+1的时候，如果arr[K+1]小于arr中最小的值，那么就丢掉不管，如果arr[K+1]大于arr中最小的值，那么就把arr[K+1]和数组中最小的值进行交换，然后再读取K+2个数。这样就能解决这个问题。但是这个算法复杂度为K+(N-K)*K，K可以忽略不计，所以时间复杂度为O(KN)。那这个代码很容易就写出来。假如题目要求用到NlgK的时间复杂度，那么这里就需要使用堆这种数据结构来解决问题，而且还是小顶堆。具体思想还是和数组一样.

题10 :所有员工年龄排序

• 公司现在要对几万员工的年龄进行排序,因为公司员1工的人数非常多,所以要求排序算法的效率要非常高,你能写出这样的程序吗

• 输入:输入可能包含多个测试样例,对于每个测试案例,

• 输入的第一行为-一个整数n(1<= n<=1000000) :代表公司内员工的人数。

• 输入的第二行包括n个整数:代表公司内每个员工的年龄。其中，员工年龄age的取值范围为(1<=age<=99)。

• 输出:对应每个测试案例，

• 请输出排序后的n个员工的年龄，每个年龄后面有-一个空格。

采用计数排序，计数排序适用于数据范围小且已知

题11 :数组能排成的最小数(特殊排序)

思路： 这题本质上，竟然是一个排序题，只是在排序时，需要重新制定排序规则
例如 "3" 和 "30" 303 < 330
排序规则可得：
如果x + y > y + x, 那么 x 的权值就大于y
反之亦然

思想冒泡排序，两两组合比较

例子：{3 32 321}

3 32 比较 332 323 ——》 32 3 321

3 321 比较 3321 3213 ——》32 321 3

32 321 比较 32321 32132——》321 32 3

"""
剑指offer题1，关于数组排成最小数
其实这是一个排序问题，相比大家都知道答案，根据AB和BA比较，谁小以谁的顺序为升序，
即[A,B,C,D]进行组合，若已知ABCD升序排列，即AB

题12 :数组的包含

输入两个字符串str1和str2 ,请判断str1中的所有字符是否都存在与str2中

1.遍历查找是否存在，有一个不存在就return -1

2.排序后二分查找