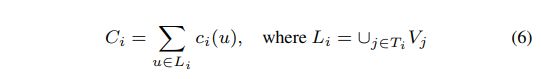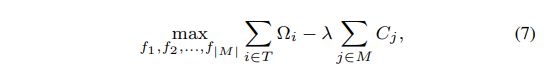PPI数据集示例项目学习图神经网络

PPI数据集：

参考：https://blog.csdn.net/weixin_43580130/article/details/116449062

PPI(生物化学结构) 网络是蛋白质相互作用（Protein-Protein Interaction,PPI）网络的简称，在GCN中主要用于节点分类任务
PPI是指两种或以上的蛋白质结合的过程，通常旨在执行其生化功能。一般地，如果两个蛋白质共同参与一个生命过程或者协同完成某一功能，都被看作这两个蛋白质之间存在相互作用。多个蛋白质之间的复杂的相互作用关系可以用PPI网络来描述。

PPI数据集共24张图，每张图对应不同的人体组织，平均每张图有2371个节点，共56944个节点818716条边，每个节点特征长度为50，其中包含位置基因集，基序集和免疫学特征。基因本体基作为label(总共121个)，label不是one-hot编码。

valid_feats.npy文件保存节点的特征，shape为(56944, 50)(节点数目，特征维度)，值为0或1，且1的数目稀少；
ppi-class_map.json为节点的label文件，shape为(121, 56944),每个节点的label为121维；
ppi-G.json文件为节点和链接的描述信息，节点：{“test”: true, “id”: 56708, “val”: false}, 表示节点id为56708的节点是否为test集或者val集，链接：“links”: [{“source”: 0, “target”: 372}, {“source”: 0, “target”: 1101}, 表示节点id为0的节点和为1101的节点之间有links。
ppi-walks.txt文件中为链接信息
ppi-id_map.json文件为节点id信息

PPI数据集代码的理解

    def __init__(
        self,
        root: str,
        split: str = 'train',
        transform: Optional[Callable] = None,
        pre_transform: Optional[Callable] = None,
        pre_filter: Optional[Callable] = None,
    ):

        assert split in ['train', 'val', 'test']

        super().__init__(root, transform, pre_transform, pre_filter)

        if split == 'train':
            self.data, self.slices = torch.load(self.processed_paths[0])
        elif split == 'val':
            self.data, self.slices = torch.load(self.processed_paths[1])
        elif split == 'test':
            self.data, self.slices = torch.load(self.processed_paths[2])

1、PPI数据集使用三个pt文件分别保存train val test，这一点值得学习。

2、使用图的库networkx处理图数据；

3、使用mask的思路处理数据集的，这一点在其他数据集的处理中也可以观察到，可以节约内存，减少数据的拷贝

data = Data(edge_index=edge_index, x=x[mask], y=y[mask])

算法原理：

参考：https://arxiv.org/abs/1707.04638

OhmNet的伪码在算法1中给出。

在第一阶段，OhmNet应用Node2vec算法（Grover和Leskovec，2016）为每个层中的每个节点构建网络邻居。给定层Gi和节点u∈Vi，该算法模拟用户定义的从节点u开始的固定长度随机游动数（算法1中的步骤4）。

在第二阶段，OhmNet使用了一种迭代方法，在该方法中，与层次结构中的每个对象相关的特征通过固定其余的特征来迭代更新。迭代方法的优点在于，它可以容易地合并为层次结构的内部对象开发的封闭形式更新（算法1中的步骤11），从而加速OhmNet算法的收敛。对于每个叶对象i，OhmNet隔离了等式（7）中优化问题中的项，这些项取决于定义函数fi的模型参数。OhmNet然后通过对fi模型参数执行一个时期的随机梯度下降（SGD1）来优化等式（6）（算法1中的步骤15）。OhmNet的两个阶段依次执行。OhmNet算法可扩展到大型多层网络，因为每个阶段都可并行化并异步执行。使用分层模型对网络层之间的依赖性进行建模的选择需要$O(|M|N)$时间，而不是需要$O(K^{2}N)$时间的完全成对模型。

等式6：

等式7：

代码实现：

参考：PyG

import os.path as osp

import torch
import torch.nn.functional as F
from sklearn.metrics import f1_score
from torch.nn import Linear

import torch_geometric.transforms as T
from torch_geometric.datasets import PPI
from torch_geometric.loader import DataLoader
from torch_geometric.nn import GCN2Conv

path = osp.join(osp.dirname(osp.realpath(__file__)), '..', 'data', 'GCN2_PPI')
pre_transform = T.Compose([T.GCNNorm(), T.ToSparseTensor()])
train_dataset = PPI(path, split='train', pre_transform=pre_transform)
val_dataset = PPI(path, split='val', pre_transform=pre_transform)
test_dataset = PPI(path, split='test', pre_transform=pre_transform)
train_loader = DataLoader(train_dataset, batch_size=2, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=2, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=2, shuffle=False)


class Net(torch.nn.Module):
    def __init__(self, hidden_channels, num_layers, alpha, theta,
                 shared_weights=True, dropout=0.0):
        super().__init__()

        self.lins = torch.nn.ModuleList()
        self.lins.append(Linear(train_dataset.num_features, hidden_channels))
        self.lins.append(Linear(hidden_channels, train_dataset.num_classes))

        self.convs = torch.nn.ModuleList()
        for layer in range(num_layers):
            self.convs.append(
                GCN2Conv(hidden_channels, alpha, theta, layer + 1,
                         shared_weights, normalize=False))

        self.dropout = dropout

    def forward(self, x, adj_t):
        x = F.dropout(x, self.dropout, training=self.training)
        x = x_0 = self.lins[0](x).relu()

        for conv in self.convs:
            h = F.dropout(x, self.dropout, training=self.training)
            h = conv(h, x_0, adj_t)
            x = h + x
            x = x.relu()

        x = F.dropout(x, self.dropout, training=self.training)
        x = self.lins[1](x)

        return x


device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(hidden_channels=2048, num_layers=9, alpha=0.5, theta=1.0,
            shared_weights=False, dropout=0.2).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
criterion = torch.nn.BCEWithLogitsLoss()


def train():
    model.train()

    total_loss = total_examples = 0
    for data in train_loader:
        data = data.to(device)
        optimizer.zero_grad()
        loss = criterion(model(data.x, data.adj_t), data.y)
        loss.backward()
        optimizer.step()
        total_loss += loss.item() * data.num_nodes
        total_examples += data.num_nodes
    return total_loss / total_examples


@torch.no_grad()
def test(loader):
    model.eval()

    ys, preds = [], []
    for data in loader:
        ys.append(data.y)
        out = model(data.x.to(device), data.adj_t.to(device))
        preds.append((out > 0).float().cpu())

    y, pred = torch.cat(ys, dim=0).numpy(), torch.cat(preds, dim=0).numpy()
    return f1_score(y, pred, average='micro') if pred.sum() > 0 else 0


for epoch in range(1, 2001):
    loss = train()
    val_f1 = test(val_loader)
    test_f1 = test(test_loader)
    print(f'Epoch: {epoch:04d}, Loss: {loss:.4f}, Val: {val_f1:.4f}, '
          f'Test: {test_f1:.4f}')

代码理解

GCN2Conv：

论文：Simple and Deep Graph Convolutional Networks (arxiv.org)

图卷积网络（GCN）是一种针对图结构数据的强大的深度学习方法。最近，GCN及其后续变体在真实世界数据集上的各个应用领域表现出了优异的性能。**尽管图卷积网络（GCN）取得了成功，但由于过度平滑的问题（ over-smoothing problem），目前的GCN模型大多是浅层网络。GCNII是普通GCN模型的扩展，具有两种简单而有效的技术：初始残差和直接映射（Initial residual and Identity mapping）。**提供了理论和经验证据，证明这两种技术有效地缓解了过度平滑的问题。实验表明，深度GCNII模型在各种半监督和全监督任务上优于最先进的方法。代码可从https://github.com/chennnM/GCNII获取。

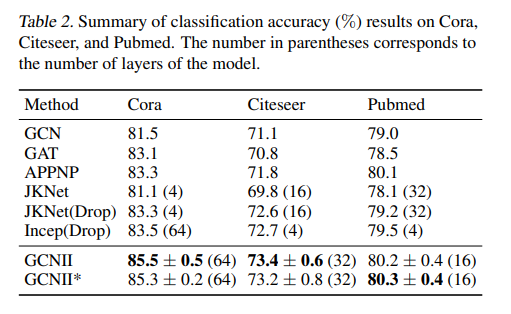
而且，在PPI数据集上面实现SOTA水平：

GCN2Conv的接口：

def __init__(self, channels: int, alpha: float, theta: float = None,
               layer: int = None, shared_weights: bool = True,
               cached: bool = False, add_self_loops: bool = True,
               normalize: bool = True, **kwargs):

‘’’
channels 输入和输出样本的size
alpha 初始的残差连接的强度
theta 超参数，用于计算直接映射的强度
layer 模型被运行的\ell层
shared_weights 是否共享权重，False：会使用不同的权重矩阵到平滑的表示和初始残差
cached True:缓存计算结果D，transductive learning scenarios下必须设置True
add_self_loops： False则不添加自环
normalize：是否添加自环和归一化
‘’’

def forward(self, x: Tensor, x_0: Tensor, edge_index: Adj,
            edge_weight: OptTensor = None) -> Tensor:
    if isinstance(edge_index, Tensor):
		...
	elif isinstance(edge_index, SparseTensor):
		...

需要注意的是：
edge_index可以接受两种形式的表示，稀疏表示和稠密表示;其中的SparseTensor可以由T.ToSparseTensor()，转变成稀疏张量，注意放在transform的最后。并且可以结合T.GCNNorm()：图归一化。pre_transform = T.Compose([T.GCNNorm(), T.ToSparseTensor()])作为PPI数据集的预处理步骤。

训练过程

Epoch: 0001, Loss: 1.9191, Val: 0.4088, Test: 0.4114
Epoch: 0002, Loss: 0.6159, Val: 0.4249, Test: 0.4259
Epoch: 0003, Loss: 0.5772, Val: 0.4379, Test: 0.4397
Epoch: 0004, Loss: 0.5610, Val: 0.4301, Test: 0.4313
Epoch: 0005, Loss: 0.5526, Val: 0.4385, Test: 0.4401
Epoch: 0006, Loss: 0.5474, Val: 0.4469, Test: 0.4491
Epoch: 0007, Loss: 0.5423, Val: 0.4494, Test: 0.4520
Epoch: 0008, Loss: 0.5371, Val: 0.4595, Test: 0.4623
Epoch: 0009, Loss: 0.5318, Val: 0.4723, Test: 0.4763
Epoch: 0010, Loss: 0.5275, Val: 0.4933, Test: 0.4979
Epoch: 0011, Loss: 0.5246, Val: 0.4837, Test: 0.4884
Epoch: 0012, Loss: 0.5214, Val: 0.4830, Test: 0.4877
Epoch: 0013, Loss: 0.5189, Val: 0.4987, Test: 0.5044
Epoch: 0014, Loss: 0.5172, Val: 0.5008, Test: 0.5068
Epoch: 0015, Loss: 0.5158, Val: 0.5069, Test: 0.5133
Epoch: 0016, Loss: 0.5133, Val: 0.4901, Test: 0.4964
Epoch: 0017, Loss: 0.5116, Val: 0.4744, Test: 0.4807
Epoch: 0018, Loss: 0.5089, Val: 0.4992, Test: 0.5062
Epoch: 0019, Loss: 0.5067, Val: 0.5103, Test: 0.5185
Epoch: 0020, Loss: 0.5045, Val: 0.5130, Test: 0.5212
807
Epoch: 0018, Loss: 0.5089, Val: 0.4992, Test: 0.5062
Epoch: 0019, Loss: 0.5067, Val: 0.5103, Test: 0.5185
Epoch: 0020, Loss: 0.5045, Val: 0.5130, Test: 0.5212
Epoch: 0021, Loss: 0.5022, Val: 0.5113, Test: 0.5198