用模型拟合New Haven市年平均气温变化并预测未来三年的温度

一、导入数据

num<-read.csv("D:\\nhtemp.csv",header = T)
num

二、画出时序图

number<-ts(num[,2],start = 1912)
number
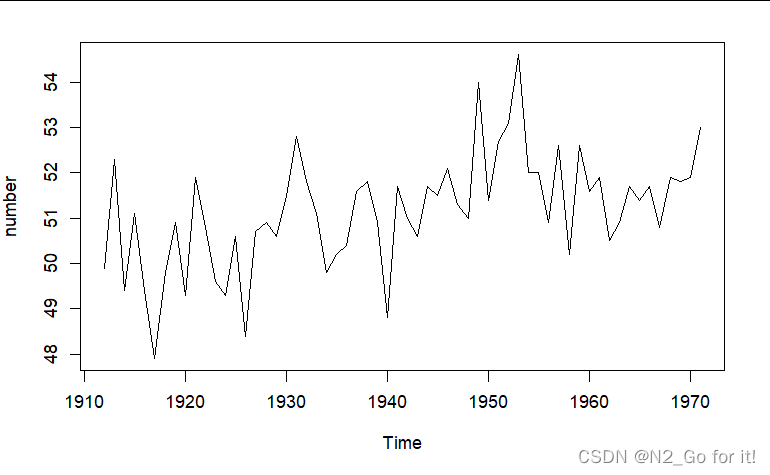
plot(number)

三、平稳性检验和白噪声检验

ADF检验

library(aTSA)
adf.test(number, nlag = 2)

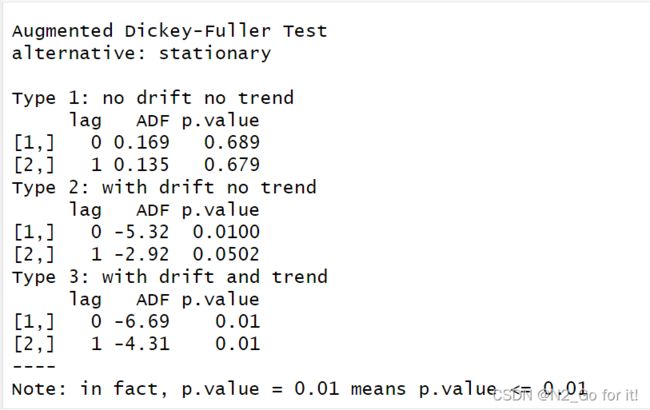从ADF检验结果上看，在95%的显著性水平下，P<0.05，拒绝原假设，该序列为平稳性序列。

白噪声检验（纯随机性检验）

lag=c()
Q.value=c()
p.value=c()
for(i in 1:6){
  test=Box.test(number,lag=i,type="Ljung-Box")
  lag[i]=i
  Q.value[i]=test$statistic
  p.value[i]=test$p.value
}  
data.frame(lag=lag,Q.value=Q.value,p.value=p.value)

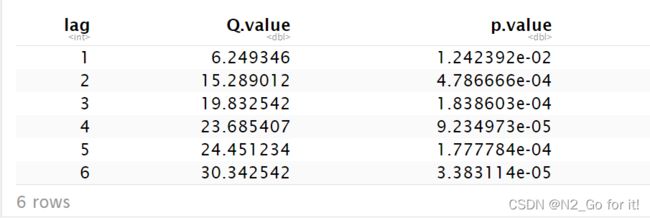
从纯随机性结果上看，p值均小于0.05，拒绝原假设，该时间序列为非白噪声序列。
从以上检验可以确认，该时间序列为平稳非白噪声序列。

四、计算ACF和PACF

par(mfrow=c(1,2))
acf(number)
pacf(number)

根据自相关图，判断该自相关图五阶拖尾或截尾，偏自相关图二阶截尾拖尾，尝试拟合AR(2)或MA(5)模型

五、模型拟合–估计模型中未知参数的值

1、AR(2)模型

fit_xAR=arima(number,order=c(2,0,0),include.mean = T,method="CSS-ML")
fit_xAR

根据上述输出结果可以得出，
φ0=51.1908*(1-0.2191-0.3178)
Xt=23.70646 + 0.2191Xt-1 + 0.3178Xt-2 + et

2、MA(5)模型

fit_xMA <- arima(number, order = c(0, 0, 5))
fit_xMA

根据上述输出结果可以得出，
xt - 51.1694 = et/(1 - 0.2737B-0.3975B^2 - 0.2655B^3 -0.0612B^4 + 0.1770B^5)

六、模型检验

一、参数显著性检验

AR(2)

t = abs(fit_xAR$coef)/sqrt(diag(fit_xAR$var.coef))
pt(t, length(number) - length(fit_xAR$coef), lower.tail = F)

结论：AR(2)模型的两个系数检验p值均很小，拒绝原假设，两个参数显著非零，保留

MA(5)

t = abs(fit_xMA$coef)/sqrt(diag(fit_xMA$var.coef))
pt(t, length(number) - length(fit_xMA$coef), lower.tail = F)

结论：MR(6)模型的系数检验p值均很小，拒绝原假设，两个参数均显著非零，保留

二、模型显著性检验

1、AR(2)

library(aTSA)
ts.diag(fit_xAR)

结论：由检验结果可知，AR（2）模型的残差序列p值均很大，不拒绝原假设，所以该模型的残差序列是白噪声序列，检验结果为拟合模型显著成立。

2、MA(5)

library(aTSA)
ts.diag(fit_xMA)

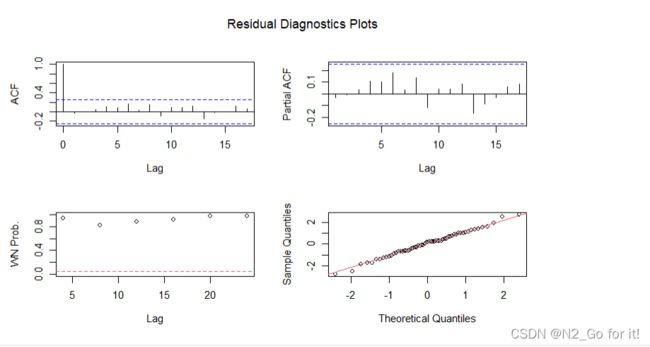
结论：由检验结果可知，MA(5)模型的残差序列p值均很大，不拒绝原假设，所以该模型的残差序列是白噪声序列，检验结果为拟合模型显著成立。
根据上述输出结果可以得出，残差序列均属于白噪声序列，则认为MA(5)模型和AR(2)模型拟合显著有效

七、用AIC准则和BIC准则评判模型的相对优劣

data.frame(AIC(fit_xMA), AIC(fit_xAR), BIC(fit_xMA), BIC(fit_xAR))

结论：根据上述结果得出，AR(2)模型的AIC和BIC值比MA(5)模型的值小，所以可以认为AR(2)模型相对最优。

八、预测未来三年温度

library(forecast)
fore_AR <- forecast(fit_xAR, h = 3)
fore_AR

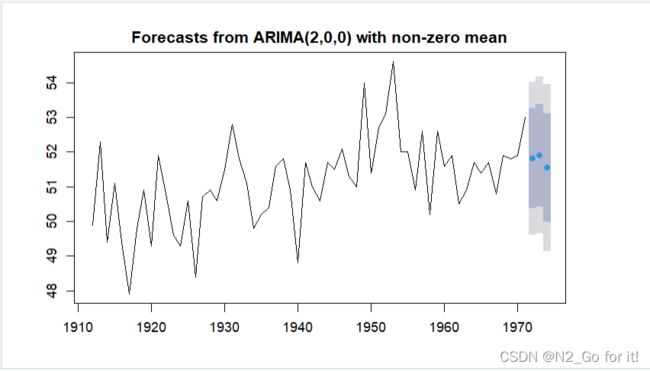
plot(fore_AR)

手动预测：Xt=23.70646+0.2191Xt-1+0.3178Xt-2+ et

当t=1972时，Xt=23.70646+0.2191*53+0.317851.9=51.81258

当t=1973时，Xt=23.70646+0.219151.81258+0.317853=51.902

当t=1974时，Xt=23.70646+0.219151.902+0.317851.81258=51.54423

模型预测未来三年的温度分别为：

1972：51.81253

1973：51.90197

1974：51.54419

比较上述两个预测结果，可以发现结果相查不大。