【深度学习】Layer Normalization

【深度学习】Batch Normalization_littlemichelle-CSDN博客

与BN的原理一致，只是归一化的对象不同。

目录

Normalization

Batch Normalization

Batch Normalization的优势、劣势

Layer Normalization

---

CNN为什么要用BN， RNN为何要用layer Norm？ - 子不语的回答 - 知乎

Normalization

不管是Batch Normalization还是Layer Normalization，Normalization的目的是为了把输入转化成均值为0方差为1的数据。换句话说，这里的Normalization其实应称为Standardization（标准化），而不是Normalization（归一化）。

Normalization一般是在把数据送入激活函数之前进行的，目的是希望输入数据不要落在激活函数的饱和区。

Batch Normalization

Batch Normalization是用来解决“Internal Covariate Shift”问题的，其计算如下图所示：对于神经元 k ，假设某个 Batch 包含 n 个训练实例，那么每个训练实例在神经元 k 都会产生一个激活值，也就是说 Batch 中 n 个训练实例分别通过同一个神经元 k 的时候产生了 n 个激活值，BatchNorm 的集合 S ，选择入围的神经元就是这 n 个同一个神经元被 Batch 不同训练实例激发的激活值。划定集合 S  的范围后，计算其均值与方差，进行标准化即可。

重要的结论：1、ICS不是训练不好的真正原因；2、在更规范的定义下，BN不能减少ICS。

最后一步是进行尺度缩放和偏移操作，目的是实现恒等变换，使其可以变换回原始的分布。此举亦可补偿网络的非线性表达能力，因为经过标准化之后，偏移量丢失。当gamma等于标准差，β等于均值的时候，就实现了恒等变换。

从某种意义上来说，gamma和beta代表的其实是输入数据分布的方差和偏移。对于没有BN的网络，这两个值与前一层网络带来的非线性性质有关，而经过变换后，就跟前面一层无关，变成了当前层的一个学习参数，这更加有利于优化并且不会降低网络的能力。

• Batch Normalization在CNN中的使用

BN层是对于每个神经元做归一化处理，甚至只需要对某一个神经元进行归一化，而不是对一整层网络的神经元进行归一化。既然BN是对单个神经元的运算，那么在CNN中卷积层上怎么办??

假如某一层卷积层有6个特征图，每个特征图的大小是100*100，这样就相当于这一层网络有100*100*6个神经元，如果采用BN，就会有100*100*6个参数γ、β，这样岂不是太恐怖了。因此卷积层上的BN使用，其实也是使用了类似权值共享的策略，把一整张特征图当做一个神经元进行处理。

CNN经过卷积后得到的是一系列的feature map，如果min-batch sizes为m，那么网络某一层输入数据可以表示为四维矩阵(m,f,p,q)，m为min-batch sizes，f为特征图个数，p、q分别为特征图的宽高。在CNN中我们可以把每个特征图看成是一个特征处理（一个神经元），因此在使用Batch Normalization，mini-batch size 的大小就是：m*p*q，于是对于每个特征图都只有一对可学习参数：γ、β。说白了吧，这就是相当于求取所有样本所对应的一个特征图的所有神经元的平均值、方差，然后对这个特征图神经元做归一化。

• Batch Normalization的优势、劣势

优点：

1. 增加了模型的泛化能力，一定程度上取代了之前的Dropout;
2. 减轻了模型对参数初始化的依赖，且可加快模型训练，提高模型精度。

不足：

1. Batch Normalization中batch的大小，会影响实验结果，主要是因为小的batch中计算的均值和方差可能与测试集数据中的均值与方差不匹配；
2. 难以用于RNN。以 Seq2seq任务为例，同一个batch中输入的数据长短不一，不同的时态下需要保存不同的统计量，无法正确使用BN层，只能使用Layer Normalization。

目前众多的实验结果表明：BN 在 MLP 和 CNN 上表现优异，但在 RNN 上效果不明显。

多提一句，关于Normalization的有效性，主流观点有：

（1）主流观点，Batch Normalization调整了数据的分布，不考虑激活函数，它让每一层的输出归一化到了均值为0方差为1的分布，这保证了梯度的有效性，目前大部分资料都这样解释，比如BN的原始论文认为的缓解了Internal Covariate Shift(ICS)问题。

（2）可以使用更大的学习率，文【3】指出BN有效是因为用上BN层之后可以使用更大的学习率，从而跳出不好的局部极值，增强泛化能力，在它们的研究中做了大量的实验来验证。

（3）损失平面平滑。文【4】的研究提出，BN有效的根本原因不在于调整了分布，因为即使是在BN层后模拟ICS，也仍然可以取得好的结果。它们指出，BN有效的根本原因是平滑了损失平面。之前我们说过，Z-score标准化对于包括孤立点的分布可以进行更平滑的调整。

Layer Normalization

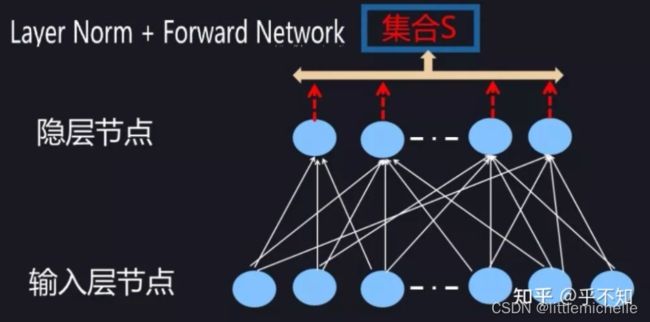
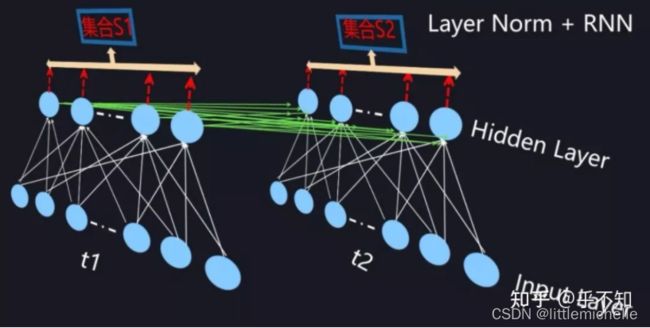
Batch Normalization是针对于在mini-batch训练中的多个训练样本提出的，为了能在只有一个训练样本的情况下，也能进行Normalization，所以有了Layer Normalization。Layer Normalization的基本思想是：用同层隐层神经元的响应值作为集合 S 的范围，来求均值和方差。而RNN的每个时间步的都有隐层，且包含了若干神经元，所以Layer Normalization可直接应用于RNN。下面是Layer Normalization的示意图，注意与之前Batch Normalization的差异，重点在于取集合 ​​​​​​​ S 的方式，得到 ​​​​​​​ S 后，求均值和方差即可。

下面是 Layer Normalization 与 RNN 的结合：

关于pytroch实现LayerNorm：

import torch
import torch.nn as nn

class LayerNorm(nn.Module):
    """亦可见nn.LayerNorm"""
    def __init__(self, features, epsilon=1e-6):
        """features: normalized_shape
            epsilon: 一个很小的数，防止数值计算的除0错误
        """
        super(LayerNorm, self).__init__()
        self.gamma = nn.Parameter(torch.ones(features))
        self.beta = nn.Parameter(torch.zeros(features))
        self.epsilon = epsilon

    def forward(self, x):
        """
        Args:
            x: 输入序列张量，形状为[B, L, D]
        """
        mean = x.mean(-1, keepdim=True)   # 在X的最后一个维度求均值
        std = x.std(-1, keepdim=True)   # 在X的最后一个维度求方差
        return self.gamma * (x - mean) / (std + self.epsilon) + self.beta