DFT的一些基本性质

DFT有许多基本性质，在这里做一个整理，主要介绍了DFT的如下性质：线性性质、平移性质、翻转性质、实数信号的对称性和奇偶性、卷积和DFT的联系、相关和DFT的联系、帕塞瓦尔定理、缩放性质、上下采样和混叠效应，以及这些性质之间的联系。DFT是数字信号处理的基石，这些性质可以帮助我们更深入的理解数字信号处理。另外，还使用了python对这些性质进行了验证，还给出了使用DFT计算相关，以及上下采样算法。

Linearity

两函数之和的傅里叶变换等于各自变换之和
$\alpha x_1+\beta x_2\leftrightarrow \alpha X_1+\beta X_2$
python测试代码如下：

import numpy as np

x1 = np.random.randint(0,10,64)
x2 = np.random.randint(0,10,64)
alpha = np.random.normal()
beta = np.random.normal()
y1 = alpha*x1+beta*x2
X1 = alpha*np.fft.rfft(x1)
X2 = beta*np.fft.rfft(x2)
Y = X1+X2
y2 = np.fft.irfft(Y)
print(np.allclose(y1,y2))

结果如下：

True

Shift Theorem

时域x(n)输入序列的时间偏移表现为与DFT结果相关的角度中的恒定相移，如果我们定义$SHIF{T}_k(x)$表示将信号右移k个样本点，那么偏移后的序列的频谱与偏移前的频谱有如下关系
$SHIF{T}_k(x)=x(n-k)$
$X_{shifted}(m)=e^{j2\pi km/N}X(m)$
即如果时域输入序列x(n)右移k个样本点，那么对应的DFT频谱$X_{shifted}(m)$是$X(m)$乘以一个恒定的相位偏移$e^{j2\pi km/N}$，同样，如果左移k个样本点，那么对应的DFT频谱则是乘以$e^{-j2\pi km/N}$
python测试代码如下：

def shift(x,N):
  p = len(x)-(N%len(x))
  x_s = np.concatenate([x[p:],x[:p]])
  return x_s
  
N = 8
l = 7
x = np.random.randint(0,10,N)
x_shift = shift(x,l)

X = np.fft.fft(x)
X_shift = np.fft.fft(x_s)*np.exp(2j*np.pi*np.arange(N)*l/N)

print(np.allclose(X,X_shift ))

结果如下：

True

Time Reversal

在离散时间系统中，我们需要考虑两种形式的时间反转。考虑六点x（n）时域序列
$x(n)=x(0),x(1),x(2),x(3),x(4),x(5)$

第一种反转是直接时间反转：
$x_s(n)=x(5),x(4),x(3),x(2),x(1),x(0)$

第二种是循环时间反转：
由于FFT的周期性特性，我们可以将x(n)时间序列描绘为一个圆上的采样，如下图所示。我们将逆时针旋转表示为正时间流，因此x(n)等间隔逆时针分布在圆上，与之前我介绍过的循环卷积中的圆的概念一样，那么循环时间反转便是围绕圆的负时间方向(顺时针方向)移动得到反转后的序列

循环时间反转后的序列：
$x_c(n)=x(0),x(5),x(4),x(3),x(2),x(1)$

用X(m)表示x(n)的DFT，反转后的序列有如下性质：
$X_s(m)=X_c(m)e^{-j2\pi m(N-1)/N}=X^{\ast }(m)e^{-j2\pi m(N-1)/N}$
python测试代码如下：

def circular_time_reversal(x):
    x_r = x.copy()
    x_r[1:] = x_r[1:][::-1]
    return x_r

def straight_time_reversal(x):
  x_s = x.copy()
  return x_s[::-1]
  
N = 8
x = np.random.randint(0,10,N)
x_ctr = circular_time_reversal(x)
x_str = straight_time_reversal(x)

X = np.fft.fft(x)
X_ctr = np.fft.fft(x_ctr).conj()
X_str = np.fft.fft(x_str).conj()*np.exp(-2j*np.pi*np.arange(N)*(N-1)/N)

print(np.allclose(X,X_ctr))
print(np.allclose(X,X_str))

结果如下：

True
True

时间反转与位移定理的关系：
将序列x(n)右移N-1个样本点然后直接时间反转等于将序列x(n)循环时间反转
对于序列x(n)，首先右移N-1个样本：
$x(n)=x(1),x(2),x(3),x(4),x(5),x(0)$
然后直接反转：
$x(n)=x(0),x(5),x(4),x(3),x(2),x(1)$

Symmetry for Real Signals

在实际工程中大多数处理的真实信号都是实信号，实信号的傅里叶变换频谱为共轭对称的，其频谱有如下性质：
实部为偶对称，虚部为奇对称：
$re\{X(-\omega )\}=re\{X(\omega )\}$
$im\{X(-\omega )\}=-im\{X(\omega )\}$
幅度为偶对称，相位为奇对称:
$|X(-\omega )=|X(\omega )|$
$\angle X(-\omega )=-\angle X(\omega )$

Real Even (or Odd) Signals

如果一个信号偶对称且为实信号，那么其对应的DTFT频谱也是偶对称且为实数，即虚部为0
与此类似，如果一个信号奇对称且为实信号，那么其对应的DTFT频谱也是奇对称且为纯虚数，即实部为0

Convolution Theorem

卷积与DFT的关系在之前有讲到，这里不再做介绍

Correlation Theorem

对于两个序列x(n)和y(n)，相关定义为：
$r(n)=\sum _{m=0}^{N-1}x(m)y(m-n)$
从相关的定义可以看出，相比卷积，相关只是少了将y反转这一步骤，卷积的计算方式是一样的，因此同样可以使用DFT来计算相关，假设序列x(n)长为M,y(n)长为N，计算相关的结果长为L=M+N-1，计算步骤如下：
1、将序列x(n)补零至L，进行傅里叶变换得到X(m)
2、将序列y(n)反转，然后补零至L，进行傅里叶变换得到Y(m)
3、计算R(m)=X(m)Y(m)，进行傅里叶逆变换得到r(n)

上面这种计算方式需要将y(n)反转，步骤稍显复杂，我们可以使用上面的移位定理和时间反转定理，不做反转，只在频域乘上一个相位偏移，步骤如下：
1、将序列x(n)和y(n)都补零至L，进行傅里叶变换得到X(m)，Y(m)
2、计算$R(m)=X(m)Y^{\ast }(m)e^{-2j\pi m(L-M)/L}$，进行傅里叶逆变换得到r(n)
python代码如下：

M = 8
N = 5
x = np.random.randint(0,10,M)
y = np.random.randint(0,10,N)
r1 = np.correlate(x,y,mode='full')
L = M+N-1
X = np.fft.fft(x,L)
Y = np.fft.fft(y,L)
R = X*Y.conj()*np.exp(-2j*np.pi*np.arange(L)*(L-M)/L)
r2 = np.fft.ifft(R,L)
print(np.allclose(r1,r2))

Parseval’s theorem

序列x(n)与其频谱有如下关系：
$\sum _{n=-\infty }^{\infty }|x[n]{|}^2=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }|X(e^{j\omega }){|}^{2}d\omega$
$\sum _{n=0}^{N-1}|x[n]{|}^2=\frac{1}{N}\sum _{m=0}^{N-1}|X(m){|}^2$

根据帕塞瓦尔定理的表达式可以看出，序列x(n)依时间域t累积的总能量与该波形的傅立叶变换X(f)在频率域f累积的总能量相等。
python测试代码如下：

N = 8
a = np.random.randint(0,10,N)
aa = np.sum(np.abs(a)**2)
A = np.fft.fft(a)
AA = np.sum(np.abs(A)**2)/N
print(np.allclose(aa,AA))

结果如下：

True

Scaling Theorem

我们将序列x(n)拉伸L倍定义为：在序列x(n)的每对样本之间插入L-1个零，以使序列拉长至原序列长度的L倍，如下图所示：

我们将频域的RepeatL次定义为将整个频谱$(-\pi \pi )$映射到$(-\pi /L,\pi /L)$，以$\omega =0$为中心并重复L次，如下图所示：

根据以上两个定义，DFT有如下定理：
$STRETC{H}_L(x)\leftrightarrow REPEA{T}_L(x)$
即时域将序列x(n)拉伸L倍，其对应的频域频谱在$(-\pi ,\pi )$上缩放并重复L次，这就是傅里叶变换的缩放定理

根据缩放定理，对于正整数L，如果我们能够实现一个截止频率为$\pi /L$的理想的低通滤波器，那么我们就实现了一个理想的上采样L倍的系统，对拉伸后的信号x(n)进行滤波，就可以实现将信号x(n)上采样L倍
python实现上采样代码如下：

fs = 16000
L = 2
T = 10
t = np.linspace(0, T, T*fs, endpoint=False)
x = signal.chirp(t, f0=0, f1=fs/2, t1=10, method='linear')

x_stretch = np.zeros(len(x)*L)
x_stretch[::L] = x

ntaps = 4097
cutoff = (1 / L)*fs
lpf = signal.firwin(ntaps,cutoff,window=('kaiser',100),fs=fs*L)
x_upsample = np.convolve(x_stretch,lpf,mode='same')

fig, axes = plt.subplots(nrows=3, ncols=1)
f, t, Sxx = signal.spectrogram(x, fs=fs, nfft=512)
axes[0].set_title("x")
axes[0].pcolormesh(t, f, Sxx)

f, t, Sxx = signal.spectrogram(x_stretch, fs=fs*L, nfft=512)
axes[1].set_title("x_stretch")
axes[1].pcolormesh(t, f, Sxx)

f, t, Sxx = signal.spectrogram(x_upsample, fs=fs*L, nfft=512)
axes[2].set_title("x_upsample")
axes[2].pcolormesh(t, f, Sxx)

plt.show()

结果如图：

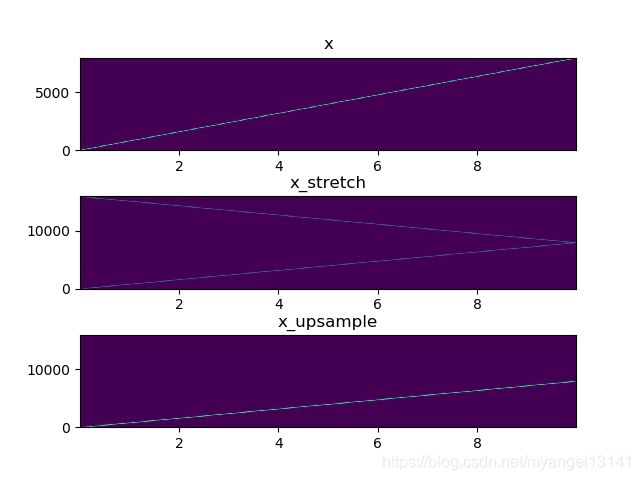
可以看到，补零后的信号x_stretch相比原信号x，在频谱上被缩放了，当通过了低通滤波后，便实现了信号的上采样

Downsampling and Aliasing

我们将信号x(n)下采样M倍定义为：在序列x(n)中只提取M倍时的样本，即
$DOWNSAMPL{E}_{M,n}(x)=x(Mn)$

根据采样定理，采样率必须高于信号最高频率的2倍，否则会发生频域混叠，当我们对信号进行下采样以降低其采样率时，就会发生混叠。

$DOWNSAMPL{E}_M(x)\leftrightarrow \frac{1}{M}ALIA{S}_M(X)$
其中:
$ALIA{S}_{M,\omega }=\sum _{m=0}^{M-1}X(\omega +k\frac{2\pi }{M})$

对于$\omega \in [-\pi ,\pi )$，其中$m\ne 0$为混叠分量
根据混叠定理，如果我们要对一个信号进行M倍下采样并且无混叠，我们必须将信号首先通过一个截止频率为$\pi /M$的理想低通滤波器
python实现下采样代码如下：

fs = 48000
M = 4
T = 10
t = np.linspace(0, T, T*fs, endpoint=False)
x = signal.chirp(t, f0=0, f1=fs/2, t1=10, method='linear')

ntaps = 4097
cutoff = fs/(M*2)
lpf = signal.firwin(ntaps,cutoff,window=('kaiser',100),fs=fs)
x_lp = np.convolve(x,lpf,mode='same')

x_aliasing = x[::M]
x_downsample = x_lp[::M]

fig, axes = plt.subplots(nrows=3, ncols=1)

f, t, Sxx = signal.spectrogram(x, fs=fs, nfft=512)
axes[0].set_title("x")
axes[0].pcolormesh(t, f, Sxx)

f, t, Sxx = signal.spectrogram(x_aliasing, fs=fs/M, nfft=512)
axes[1].set_title("x_aliasing")
axes[1].pcolormesh(t, f, Sxx)

f, t, Sxx = signal.spectrogram(x_downsample, fs=fs/M, nfft=512)
axes[2].set_title("x_downsample")
axes[2].pcolormesh(t, f, Sxx)

plt.show()

结果如图：

可以看到，在不进行低通滤波的情况下直接下采样的信号x_aliasing相比低通滤波后再进行下采样后的信号，x_aliasing出现了混叠

更一般化，任何采样率的转换$\rho =L/M$都可以首先通过时域拉伸L倍，然后经过截止频率为$\pi /MAX(L,M)$的理想低通滤波器，然后再通过下采样M倍来实现