强化学习蘑菇书Easy RL 第四五章

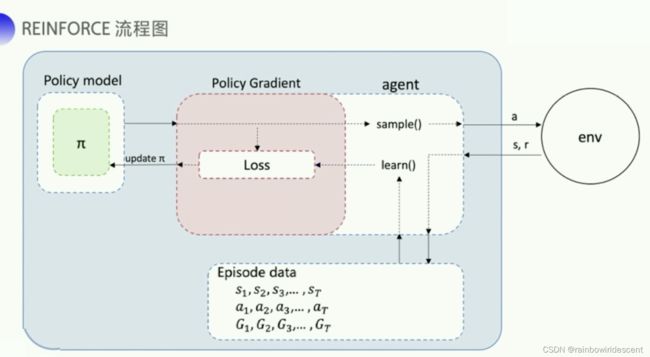
7.20更新，（这两天进度略慢，基本只学了第四章，还没学完，简单记录下吧！）首先我们必须要明确的一个概念，RL有三个组成部分：

• 演员 actor
• 环境 environment
• 奖励函数 reward function

其中，环境和奖励函数是无法控制的，而是开始学习之前给定的，所以，只能做的就是调整演员的policy，使得reward最大。同时，演员的策略决定action。
如果用深度学习来做RL的话，策略π就是一个网络，中间会有一些θ的参数。
智能体看到的就是网络的输入，他也会影响我们训练的结果。输入是智能体看到的画面，通常由像素组成，而输出是可以执行的action，在神经网络里，有几个action，就有几个神经元。

策略梯度

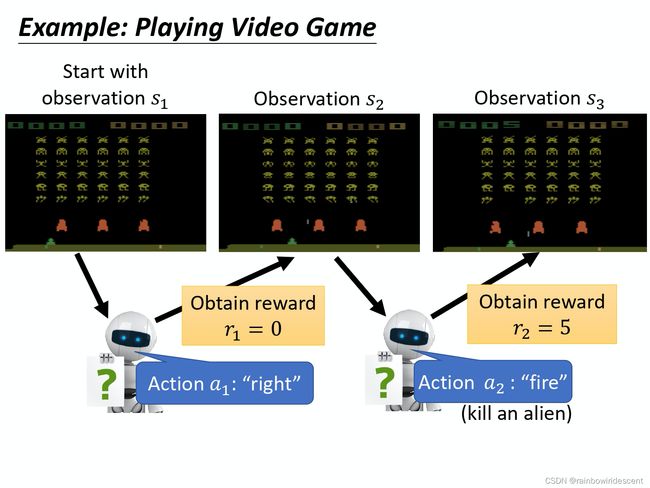
**策略梯度是一个会花很多时间来采样数据的算法，大多数时间都在采样数据。**在一场游戏中，我们把环境输出的s与演员输出的动作a组合起来成为一条轨迹，
可以得到：

$\text{ Trajectory }\tau =\left\{s_1,a_1,s_2,a_2,\cdots ,s_t,a_t\right\}$

给定演员的参数θ，可以计算每一个轨迹发生的概率：

$\begin{array}{rl}{p}_{\theta }(\tau )& =p\left(s_1\right)p_{\theta }\left(a_1\mid s_1\right)p\left(s_2\mid s_1,a_1\right)p_{\theta }\left(a_2\mid s_2\right)p\left(s_3\mid s_2,a_2\right)\cdots \\ & =p\left(s_1\right)\prod _{t=1}^T{p}_{\theta }\left(a_t\mid s_t\right)p\left(s_{t+1}\mid s_t,a_t\right)\end{array}$

通过上面的式子可以知道的事，可以计算某一个episode里面出现这样的轨迹的概率有多大，每一条轨迹出现的概率取决于环境的动作和智能体的动作。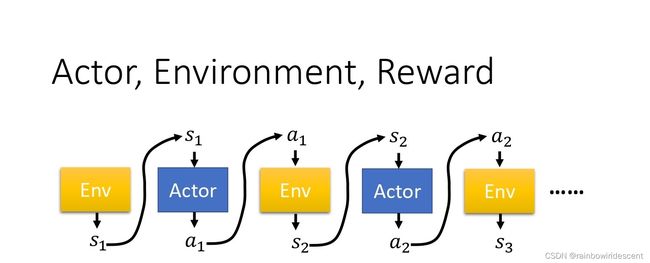
在某一场游戏里面， 某一个回合里面，我们会得到 R。我们要做的事情就是调整演员内部的参数 θ， 使得 R 的值越大越好。 但实际上奖励并不只是一个标量，奖励其实是一个随机变量。R 其实是一个随机变量，因为演员在给定同样的状态会做什么样的行为，这件事情是有随机性的。
这个地方，我们怎么处理呢，我的理解是，轨迹Trajectory的概率是不一样的，这取决于在的某一个episode里面，是不是游戏很快over了，如果over了就说明对应trajectory的p很小，所以每一个轨迹trajectory对应的奖励是不一样的，总的reward必须对于trajectory出现的概率进行加权，也就是期望值。因此，我们得到一个expected reward的总值：

${\bar{R}}_{\theta }={\sum }_{\tau }R(\tau )p_{\theta }(\tau )=E_{\tau \sim p_{\theta }(\tau )}[R(\tau )]$

在这里我们通常使用的方法就是gradient ascent来max这个expected reward。
说一下什么是梯度上升，通常来说，在中学里，我们学的导数是求一个可以写出表达式函数的极值的方法，但是，有时候有些函数即使能够写出表达式，求得的导数依然不是极值，这种情况我们通常就会使用迭代的方法来解，也就是最优化算法，引入一个α作为步长（MACHINE LEARNING中）。通常来说也可以理解为求偏导。
（这地方不放公式了，如果有疑问也可以百度一下）。
组合一下下面几个公式，我们可以把最终的trajectory求和后写成expected value最终的值：

注意一下，上面这张图片的最后一行公式，是怎么推导的呢？

$\begin{array}{rl}& =E_{\tau \sim p_{\theta }(\tau )}\left[R(\tau )\nabla \log p_{\theta }(\tau )\right]\approx \frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)\nabla \log p_{\theta }\left({\tau }^n\right)\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R\left({\tau }^n\right)\nabla \log p_{\theta }\left(a_t^n\mid s_t^n\right)\end{array}$

这里特别要说明的就是，得到的这个期望值是没法计算的，所以需要用采样的方式采样N个trajectory并计算每一个值，然后再把每一个值加起来，得到梯度。用这个updated gradient去更新agent。
（具体公式推导下面还是列一下。。）

$\begin{array}{rl}\nabla \log p_{\theta }(\tau )& =\nabla \left(\log p\left(s_1\right)+\sum _{t=1}^T\log p_{\theta }\left(a_t\mid s_t\right)+\sum _{t=1}^T\log p\left(s_{t+1}\mid s_t,a_t\right)\right)\\ & =\nabla \log p\left(s_1\right)+\nabla \sum _{t=1}^T\log p_{\theta }\left(a_t\mid s_t\right)+\nabla \sum _{t=1}^T\log p\left(s_{t+1}\mid s_t,a_t\right)\\ & =\nabla \sum _{t=1}^T\log p_{\theta }\left(a_t\mid s_t\right)\\ & =\sum _{t=1}^T\nabla \log p_{\theta }\left(a_t\mid s_t\right)\end{array}$

Note: 两个p都来自于env，而一个p_θ来自于环境，由于两个p都与环境无关，所以它们对应的log再取梯度都等于0，上式就可以只化成p_θ的梯度。
如何理解下面？在采样到的数据里面，s和a在某个时刻t应该是trajectory的一个状态动作对，我们根据trajectory得到的奖励来增加or降低该轨迹的概率，如果reward正，就增加；reward负，就减少。

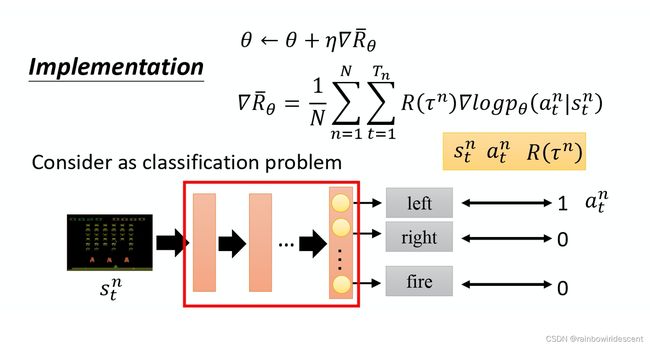
由上图我们也可以知道，为了更新，代入这个总的expected reward的公式里面，我们采样时，要搜集很多的s_t和a_t的动作对。更新参数θ也需要一个对应的learning rate，更新的θ应该是原来的θ加上梯度，而学习率调整可以用Adam方法。（关于Adam再单独出一篇博客。。。。）
你要拿你的 agent，它的参数是θ，去跟环境做互动， 也就是拿你已经训练好的 agent 先去跟环境玩一下，先去跟那个游戏互动一下， 互动完以后，你就会得到一大堆游戏的纪录。同时，和环境的互动有随机性。。。
你就可以把采样到的东西代到这个梯度的式子里面，把梯度算出来。也就是把这边的每一个 s 跟 a 的对拿进来，算一下它的对数概率(log probability)。你计算一下在某一个状态采取某一个动作的对数概率，然后对它取梯度，然后这个梯度前面会乘一个权重，权重就是这场游戏的奖励。 有了这些以后，你就会去更新你的模型。
这就是大概PG的一个流程。。。
注意：一般PG采样的数据，只能用一次，更新参数后，要丢掉原始数据，重新采样，再去更新参数。
说几点注意的实现的细节：

• 类似于一个分类问题，目标函数是最小化交叉熵，我们这里是最大化likelihood
• 强化学习与分类问题不同的地方时姚成一个权重
• 每一次训练数据要进行加权

策略梯度实现技巧

（这部分时间原因，后面会补充上细节）

1. 添加基线
2. 分配合适的credit

REINFORCE 算法

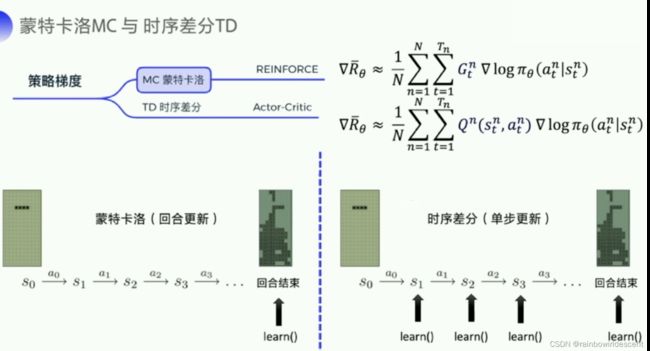
上一章也学习过蒙特卡洛和时序差分的区别，蒙特卡洛一个回合更新一次，时序差分一个步骤更新一次，所以时序差分的更新频率更高，它也使用Q函数来金斯表示未来的总奖励。下图也给出了两种不同的expected reward的式子。

Policy gradient methods can be implemented using the log_prob() method, when the probability density function is differentiable with respect to its parameters. A basic method is the REINFORCE rule:

$\Delta \theta =\alpha r\frac{\partial \log p\left(a\mid {\pi }^{\theta }(s)\right)}{\partial \theta }$

补一个代码：

probs = policy_network(state)
m = Categorical(probs)
action = m.sample()
next_state, reward = env.step(action)
loss = -m.log_prob(action) * reward
loss.backward()

近端策略优化PPO

很重要的一个概念是importance sampling：
概率密度函数提供的概率分部信息来生成随机变量的取值就是采样。
没学完。。。
明天接着补好了（最近三天一直在忙暑期课程）
害，加油吧。

Reference：
【1】https://datawhalechina.github.io/easy-rl/#/chapter4/chapter4
【2】王琦等，Easy RL蘑菇书，强化学习教程
【3】pytorch官方文档