深度学习入门基于python的的理论与实现（学习笔记）.第六章 与学习相关的技巧（第一部分）

6.1 参数的更新：
神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题，解决这个问题的过程称为最优化（optimization）。
在之前的学习中，我们为了找到最优参数，将参数的梯度（导数）作为了线索。使用参数的梯度，沿梯度方向更新参数，并重复这个步骤多次，从而逐渐靠近最优参数，这个过程称为随机梯度下降法（stochastic gradient descent），简称SGD。

• SGD：
  表达式为：
  
  python的实现代码为：

class SGD():
	def __init__(self,lr):
		self.lr = lr
	def updata(self,params,grads):
		for key  in params.key():
			params[key] -= self.lr * grads[key]
		

 - SGD的缺点：
 如果函数的形状非均向（anisotropic），比如呈延伸状，搜索的路径就会非常低效。因此需要一个比单纯朝梯度方向前进的SGD更聪明的方法。SGD低效的根本原因是，梯度的方向并没有指向最小值的方向。
 例如对于下图问题

在俯视图中等间距地标出梯度，

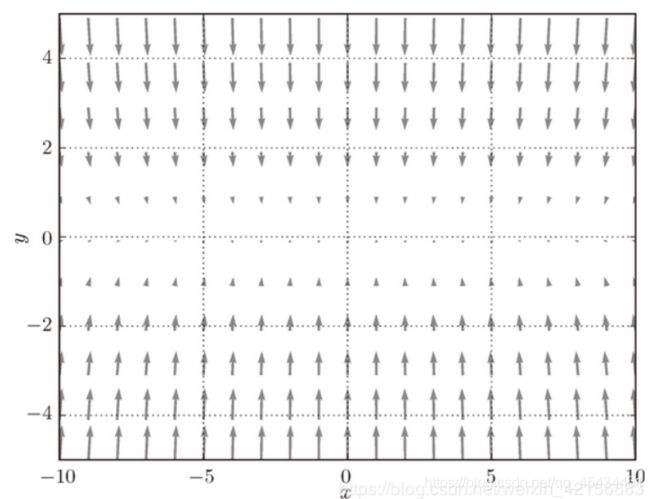
可见，梯度在x方向上的分量非常小，这将导致SGD得花很长时间才能在x方向上移动到原点处。如图

我们对SGD方法进行改进，产生了Momentum，AdaGrad和Adam法。

• Momentum：
  Momentum一词，来自于物理学中的动量。此方法中用数学表示为：
  
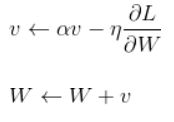
  物理意义为：可见，矩阵v的引入赋予了参数更新一定的惯性。整个过程好像许多初始位置不同的台球在有摩擦有凹陷的台球桌上的运动，可以想象，最后台球都会静止在某个局部极小值处。
  代码实现为

class Momentum():
	def __init__(self,lr,momentum):
		self.lr = lr
		self.v = None
		self.momentum =  momentum
	def updata(self,params,grads):
		if self.v == None:
			for key,val in params.items:
				self.v[key] = np.zeros_like(val)
		for key in params.key():
			self.v[key] = self.momentum * self.v - self.lr * grads[key]
			params[key] += self.v[key]

用此方法最优化路径为：

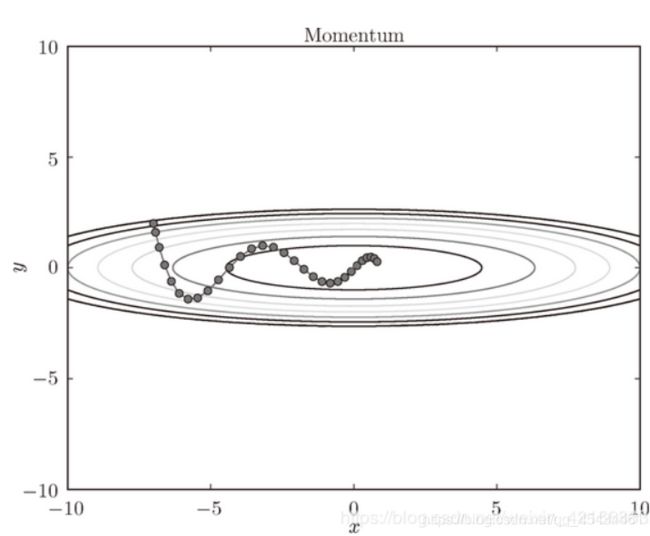
由于x方向的向心速度可以叠加，小球更快地到达了原点。

• AdaGrad

  在神经网络的学习中，学习率的值很重要。学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。
  在设定学习率的技巧中，有一种称为学习率衰减（learningrate decay），即随着学习进行，使学习率逐渐减小。实际上，一开始多学，然后逐渐少学的方法，在神经网络的学习中经常被使用。
  逐渐减小学习率的想法，相当于将”全体“参数的学习率值一起降低。而AdaGrad进一步发展了这个想法，针对”一个一个“的参数，赋予其”定制“的值。
  数学表示为：
  
  和前面的SGD一样，W表示要更新的权重参数，表示损失函数关于W的梯度，表示学习率。这里出现了新变量h，看第一个式子可知，其保存了以前所有梯度的平方和（表示矩阵对应位置相乘）。然后，在更新参数时，通过乘以，就可以调整学习的尺度。这意味着，参数的元素中变动较大（被大幅更新）的元素的学习率将变小。也就是说，可以按照参数的元素进行学习率衰减，使变动大的参数的学习率逐渐减小。

AdaGrad会记录过去所有梯度的平方和。因此，学习越深入，更新的幅度就越小。实际上，如果无止境的学习，h的值会越来越大，导致2式的后一部分趋于0，则参数将不再更新。为了改善这个问题，可以使用RMSProp方法。RMSProp方法不是将过去所有的梯度一视同仁地相加，而是逐渐地遗忘过去的梯度，在做加法运算时将新梯度的信息更多地反映出来。这种操作从专业上讲，称为“指数移动平均”，呈指数函数式地减小过去的梯度的尺度。
python代码实现过程为：

class AdaGrad():
	def __init__(self,lr,h):
		self.lr = lr
		self.h = None
	def updata(self,params,grads):
		if self.h == None:
			self.h = {}
			for key, val in params.items:
				self.h[key] = np.zeros_like(val)
		for key in params.key():
			self.h[key] += params[key] * params[key]
			params[key] -=  self.lr * grads[key]/ np.sqrt(self.h[key] + 1e-7)

关键点在于最后一行加上了微小值1e-7。这是为了防止当self.h[key]中有0时。将0用作除数的情况。在很多深度学习的框架中，这个微小值也可以设定为参数，但这里这个值是个固定值。
尝试用AdaGrad解决前面SGD出现的问题，结果如下：

可以看到，函数的值高效地向着最小值移动。由于y轴方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整，减小更新的步伐。因此，y轴方向上的更新程度被减弱，“之”字形的变动程度进一步衰减。

• Adam
  Momentum参照小球在碗中滚动的物理规则进行移动，AdaGrad为参数的每个元素适当地调整更新步伐。Adam是将这两个方法融合在一起。

通过组合前面两个方法的优点，有望实现参数空间的高效搜索。此外，进行超参数的“偏置矫正”也是Adam的特征。

根据Adam论文中的描述Adam的数学表达如下：

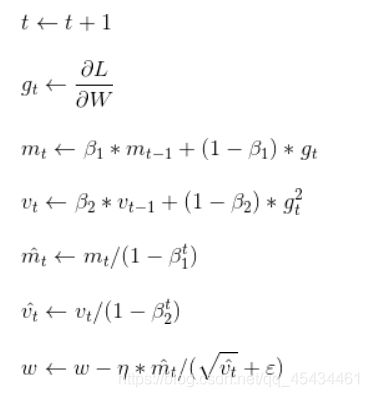
其中就是目标函数对待更新参数w的梯度，就是前面的微小值1e-9。

这里有一个记录更新次数的参数t，表示第几次调用update函数。

原文中提到，Adam会设置3个超参数。一个是学习率，另外两个是一次momentum系数和二次momentum系数。根据论文，标准的设定值是是0.9，是0.999。

根据原书中代码实现方案，Adam的数学表达如下：

上述两种表示乍一看似乎很不一样，不过把第二种进行一下因式分解和参数代换，很容易可以和第一种方式对应上。我亲自推理了下，已经确保没有问题了。不过还是推荐去读下Adam论文，对该方法的解读。
原书中python的实现为：

class Adam:
 
	def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
		self.lr = lr
		self.beta1 = beta1
		self.beta2 = beta2
		self.iter = 0
		self.m = None
		self.v = None
 
	def update(self, params, grads):
		if self.m is None:
			self.m, self.v = {}, {}
			for key, val in params.items():
				self.m[key] = np.zeros_like(val)
				self.v[key] = np.zeros_like(val)
 
		self.iter += 1
		lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
 
		for key in params.keys():
			self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
			self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
 
			params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

然后尝试用Adam参数优化方法解决SGD遇到的问题，效果如下：

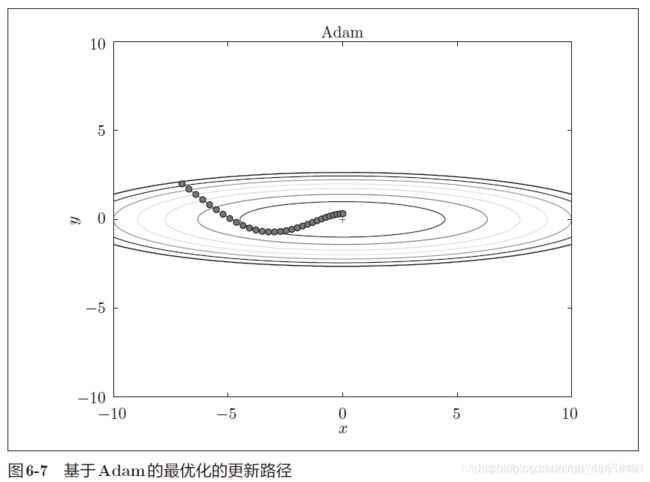
• 四种方法的对比和选择：
  
  如图所示，根据使用的方法不同，参数更新的路径也不同。只看这个图似乎AdaGrad是最好的，但要注意，结果会根据实际问题的变化而变化。而且，超参数的设置不同，结果也会发生变化。目前这4种方法各有各的特点，都有各自擅长解决的问题饿不擅长解决的问题。

还有很多其它参数优化方法，这里暂未提到。