点云 3D 目标跟踪 - AB3DMOT（IROS 2020, ECCVW 2020）

声明：此翻译仅为个人学习记录

文章信息

• 标题1：3D Multi-Object Tracking: A Baseline and New Evaluation Metrics (IROS 2020)
• 链接1：https://arxiv.org/pdf/1907.03961.pdf
• 标题2：AB3DMOT: A Baseline for 3D Multi-Object Tracking and New Evaluation Metrics (ECCVW 2020)
• 链接2：https://arxiv.org/pdf/2008.08063.pdf
• 作者：Xinshuo Weng, Jianren Wang, David Held and Kris Kitani
• 文章代码：https://github.com/xinshuoweng/AB3DMOT

摘要

  3D多目标跟踪（MOT）是自动驾驶和辅助机器人等许多应用的重要组成部分。最近关于3D MOT的工作侧重于开发精确的系统，而不太注重实际考虑，例如计算成本和系统复杂性。相比之下，这项工作提出了一个简单的实时3D MOT系统。我们的系统首先从LiDAR点云获得3D检测。然后，使用3D卡尔曼滤波器和匈牙利算法的直接组合进行状态估计和数据关联。此外，3D MOT数据集（如KITTI）评估2D空间中的MOT方法，标准化的3D MOT评估工具缺失，无法公平比较3D MOT方法。因此，我们提出了一种新的3D MOT评估工具以及三种新的指标，以全面评估3D MOT方法。我们表明，尽管我们的系统采用了经典MOT模块的组合，但我们在两个3D MOT基准（KITTI和nuScenes）上实现了最先进的3D MOT性能。令人惊讶的是，尽管我们的系统不使用任何2D数据作为输入，但我们在KITTI 2D MOT排行榜上取得了竞争性的表现。我们提出的系统在KITTI数据集上以207.4 FPS的速度运行，在所有现代MOT系统中实现了最快的速度。为了鼓励标准化3D MOT评估，我们的系统和评估代码在https://github.com/xinshuoweng/AB3DMOT。

1. 引言

  MOT是许多实时应用的重要组件，如自动驾驶[1]、[2]和辅助机器人[3]、[4]。由于目标检测的进步[5]–[8]，MOT取得了很大进展。例如，对于KITTI[9]2D MOT基准上的汽车类别，MOTA（多目标跟踪精度）在短短两年内从57.03[10]提高到84.04[11]！虽然我们对这一进展感到鼓舞，但我们发现，我们对创新和准确性的关注是以计算效率和系统简单性等实际因素为代价的。最先进的方法通常需要大量的计算成本[12]-[15]，这使得实时性能成为一个挑战。此外，现代MOT系统通常非常复杂，并不总是清楚系统的哪个部分对性能贡献最大。例如，领先的作品[14]–[16]具有实质上不同的系统管线，但性能上只有微小的差异。在这些情况下，模块化比较分析非常具有挑战性。

  为了为比较分析提供标准的3D MOT基线，我们采用了一种设计高效且简单的经典方法——卡尔曼滤波器[17]（1960年）和匈牙利方法[18]（1955年）。具体而言，我们的系统使用现成的3D目标检测器从LiDAR点云获得3D检测[6]。然后，使用3D卡尔曼滤波器（具有恒定速度模型）和匈牙利算法的组合进行状态估计和数据关联。与在2D空间[19]或鸟瞰图[20]中定义滤波器状态空间的其他基于滤波器的MOT系统不同，我们将目标的状态空间扩展到3D空间，包括3D位置、3D大小、3D速度和航向方向。

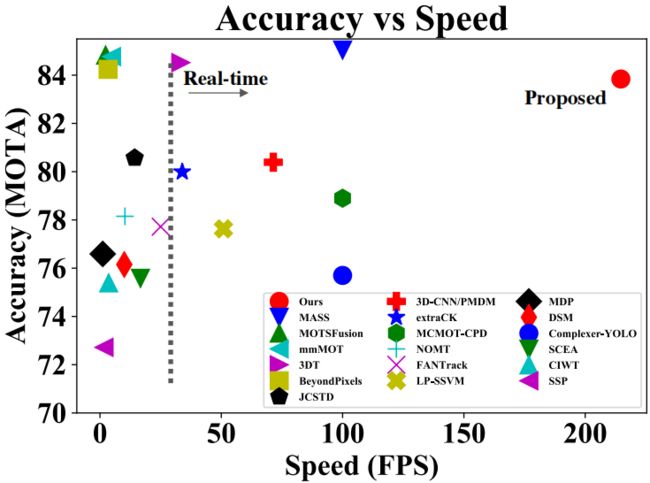
图1. KITTI 2D MOT排行榜上现代2D和3D MOT系统的MOTA。越高越右越好。我们的3D MOT系统在2D MOT评估中实现了具有竞争力的MOTA，同时速度最快。

  我们的实证结果令人担忧。虽然我们系统中的模块组合很简单，但我们在标准3D MOT数据集上实现了最先进的3D MOT性能：KITTI和nuScenes。令人惊讶的是，尽管我们的系统不使用任何2D数据作为输入，但我们在KITTI 2D MOT排行榜上也取得了竞争性的表现，如图1所示。我们假设，我们的3D MOT系统的强大2D MOT性能可能是因为3D中的跟踪比2D中的跟踪能够更好地解决深度模糊，并导致更少的失配。此外，由于我们系统的高效设计，它在KITTI数据集上以207.4 FPS的速度运行，实现了现代MOT系统中最快的速度。很明显，这项工作的贡献不是创新3D MOT算法，而是与最基本但最强大的基线相比，提供了现代3D MOT系统的更清晰的画面，其结果在整个社区都很重要。

  除了3D MOT系统，我们还观察到了3D MOT评估中的两个问题：（1）标准MOT基准（如KITTI数据集）仅支持2D MOT评估，即图像平面上的评估。目前还没有在三维空间中评估3D MOT系统的工具。在KITTI数据集上，评估3D MOT方法的惯例是将3D MOT结果投影到图像平面，然后使用KITTI 2D MOT评估工具。然而，我们认为，这将阻碍3D MOT系统的未来进展，因为在图像平面上的评估不能提供3D MOT方法的公平比较，例如，在3D中实现更好跟踪的系统不一定在2D MOT评估中具有更高的性能。为了克服这个问题，我们提出了一种MOT评估工具，该工具使用3D度量直接评估3D空间中的MOT系统；（2） MOTA和MOTP等常用MOT度量不考虑被跟踪目标的置信度得分。因此，用户必须手动选择阈值，并筛选出分数较低的跟踪目标。然而，选择最佳阈值需要付出不小的努力。此外，单一阈值的评估使我们无法了解MOT系统的全部精度和精度。为了解决这个问题，我们提出了三个新的积分度量来总结MOT方法在多个阈值上的性能。我们希望我们的新评估工具（包括度量）将作为未来3D MOT评估的标准。我们的贡献总结如下：

1） 我们提出了一种用于在线应用的基于3D卡尔曼滤波器的精确实时3D MOT系统；

2） 我们提出了一种新的3D MOT评估工具以及三种新的度量标准，以标准化3D MOT评价；

3） 我们的3D MOT系统在标准3D MOT数据集上实现了S.O.T.A.性能和最快速度。

2. 相关工作

2D多目标跟踪。最近的2D MOT系统可以基于数据关联分为批处理和在线方法。批处理方法试图从整个序列中找到全局最优关联。这些方法通常创建网络流图，并可以通过最小成本流算法[21]、[22]来解决。相比之下，在线方法只需要当前帧的信息，并且适用于在线应用。在线方法通常将数据关联表述为二分图匹配问题，并使用匈牙利算法解决[18]，[19]。除了使用匈牙利算法，现代在线方法还设计了深度关联网络[15]，[23]，可以使用神经网络构建关联。我们提出的系统属于在线方法的范畴。为了简单设计和实时效率，我们不使用神经网络，只采用匈牙利算法。

  为了实现数据关联，设计适当的成本函数来度量相似性对于MOT系统至关重要。早期的工作[21]，[24]采用手工制作的特征，如空间距离和颜色直方图作为成本函数。现代方法通常使用运动模型[19]、[25]、[26]和外观特征[25]、[7]、[28]。为了简化系统，我们只使用最简单的运动模型，即恒定速度，而不使用任何外观提示。

3D多目标跟踪。3D MOT系统通常与2D MOT系统共享相同的组件。区别在于输入检测在3D空间而不是图像平面中。因此，3D MOT系统可以在没有透视失真的情况下获得3D空间中的运动和外观信息。[16] 建议将目标到相机的距离及其在3D空间中的速度估计为运动线索。[20] 使用无迹卡尔曼滤波器估计地面上的线速度和角速度。[29]提出了一种2D-3D卡尔曼滤波器，以利用来自图像和3D世界的观测。除了使用手工制作的特征，[23]、[30]–[32]还使用神经网络从数据中学习3D外观和运动特征。与先前的工作使用各种3D特征和复杂的系统不同，为了简单和高效，我们仅使用3D卡尔曼滤波器来获得3D运动提示，并将滤波器的状态空间扩展到包括3D位置、3D速度、3D大小和航向方向在内的全3D域。

3. 方法

  3D MOT的目标是在序列中关联3D检测。由于我们的系统是一个在线MOT系统，在每个时间戳，我们只需要在当前帧中进行检测，并从先前帧中获取相关轨迹。我们的系统管线如图2所示：（A）使用3D检测模块从LiDAR点云获得3D检测；（B） 3D卡尔曼滤波器预测从先前帧到当前帧的关联轨迹的状态；（C） 数据关联模块匹配来自卡尔曼滤波器的预测轨迹和当前帧中的检测；（D） 3D卡尔曼滤波器基于匹配检测更新匹配轨迹的状态；（E） 出生和废弃记忆创建新目标的轨迹，并删除消失目标的轨迹。除了预先训练的3D检测模块，我们的3D MOT系统不需要任何训练，可以直接用于推理。

A. 3D目标检测

  由于3D目标检测的进步，我们可以获得高质量的检测。在这里，我们在KITTI上使用[6]、[33]和在NuScene上使用[34]进行实验。我们直接在相应的数据集上使用他们的预训练模型。在帧t中，3D检测模块的输出是一组检测$D_t＝\{D_t^1,D_t^2,\cdot \cdot \cdot ,D_t^{nt}\}$（nt是检测次数）。每个检测Dtj，其中j∈{1，2，··，n_t}，表示为一个元组（x，y，z，θ，l，w，h，s），包括目标中心在3D空间中的位置（x，y，z），目标的3D尺寸（l，w，h），航向角θ和置信分数s。我们将在实验中展示不同的3D检测模块如何影响我们的3D MOT系统的性能。

B. 3D卡尔曼滤波器：状态预测

  为了预测从前一帧到当前帧的目标轨迹状态，我们使用与相机自我运动无关的恒定速度模型来近似目标的帧间位移。这意味着我们不明确地估计自我运动，而是依靠我们的运动模型来适应自我运动和其他目标的运动。我们将目标轨迹的状态表示为11维向量T=（x，y，z，θ，l，w，h，s，v_x，v_y，v_z），其中附加变量v_x，v_y，v_z表示三维空间中的目标速度。注意，为了简单起见，我们没有在状态空间中包括角速度v_θ，因为我们经验发现，包括角速度并不能真正提高性能。在每一帧中，前一帧$T_{t-1}＝\{T_{t-1}^1,T_{t-1}^2,\cdot \cdot \cdot ,T_{t-1}^{m_{t-1}}\}$（m_t−1是帧t-1中的轨迹数）的相关轨迹状态将根据恒定速度模型传播到帧t作为T_est：

结果，对于$T_{t-1}$中的每个轨迹$T_{t-1}^i$，其中i∈{1，2，··，m_t−1}，帧t中的预测状态为$T_{est}^i$=（x_est，y_est，z_est，θ，l，w，h，s，v_x，v_y，v_z）。

图2. 提议的系统管道：（A）3D检测模块从LiDAR点云获得3D检测D_t；（B） 3D卡尔曼滤波器在状态预测步骤期间预测到当前帧t的轨迹T_t−1的状态作为T_est；（C） 使用匈牙利算法关联检测D_t和预测轨迹T_est；（D） 基于D_match中的对应匹配检测，通过3D卡尔曼滤波器更新T_match中每个匹配轨迹的状态，以获得最终轨迹T_t；（E） 出生和废弃记录将不匹配的检测D_unmatch和不匹配的轨迹T_unmatch作为输入，并创建新的轨迹T_new。

C. 数据关联

  为了将预测的轨迹T_est与检测D_t相匹配，我们首先通过计算每对轨迹$T_{est}^i$和检测$D_t^j$之间的3D交并比（IoU）或负中心距离来构建维度为m_t−1×n_t的亲和矩阵。然后，数据关联成为一个二分图匹配问题，可以使用匈牙利算法在多项式时间内解决[18]。此外，如果3D IoU小于阈值IoU_min（或者如果使用中心距离来计算亲和矩阵，则中心距离大于阈值dist_max），我们拒绝匹配。数据关联的输出如下：

其中T_match和D_match是匹配的轨迹和检测，w_t表示匹配的数量。此外，T_unmatch和D_unmatch是不匹配的轨迹和检测。注意，T_unmatch是T_est中T_match的互补集合。类似地，D_unmatch是D_t中D_match的互补集合。

D. 3D卡尔曼滤波器：状态更新

  为了解决状态预测的不确定性，我们基于D_match中的每个轨迹的相应检测来更新T_match中每个轨迹的状态。结果，我们获得了帧t中的最终关联轨迹，$T_t=\{T_t^1，T_t^2，\cdot \cdot ，T_t^{wt}\}$。根据贝叶斯规则，每个轨迹的更新状态$T_t^k$=（x’，y’，z’，θ’，l’，w’，h’，s’，v’_x，v’_y，v’_z），其中k∈{1，2，··，w_t}是$T_{match}^k$和$D_{match}^k$状态之间的加权平均值。权重由匹配轨迹$T_{match}^k$和检测$D_{match}^k$的状态不确定性确定（详情请参考卡尔曼滤波器[17]）。

  此外，我们观察到，直接将贝叶斯更新规则应用于方向θ并不能很好地工作。例如，可能存在检测方向$D_{match}^k$与相应轨迹$T_{match}^k$的方向几乎相反的情况，即相差π。虽然我们知道这是不可能的，因为目标应该平滑移动，并且不能在一帧内改变π的方向（即，KITTI中的0.1s），但是在检测或轨迹中对方向的预测可能是错误的，这使得这种情况成为可能。因此，如果我们遵循正常状态更新规则，在这种情况下，最终轨迹$T_t^k$的方向将位于$D_{match}^k$和$T_{match}^k$方向中间的某个位置，这将导致相关轨迹和地面真相之间的低3D IoU。为了防止这个问题，我们提出了一种定向校正技术。当$D_{match}^k$和$T_{match}^k$之间的方向θ_d之差大于π/2时，我们在$T_{match}^k$中的方向上添加一个π，使得θ_d始终小于π/2，即$D_{match}^k$和$T_{match}^k$的方向大致一致，没有实质性变化。

E. 出生和废弃记录

  由于被跟踪的目标可能会离开场景，新目标可能会进入场景，因此需要一个模块来管理目标的出生和废弃。一方面，我们将所有未匹配的检测$D_{unmatch}$视为进入场景的潜在新目标。然而，为了避免创建假阳性轨迹，将不会为未匹配的检测$D_{unmatch}^p$创建新的轨迹$T_{new}^p$，直到在下一个$Bi{r}_{min}$帧中连续匹配$D_{unmatch}^p$ ，其中p∈{1，2，··，n_t−w_t}。一旦创建了新的轨迹$T_{new}^p$，我们将其状态初始化为与v_x、v_y和v_z的速度为零的最近检测$D_{unmatch}^p$相同。

  另一方面，我们将所有不匹配的轨迹$T_{unmatch}$视为离开场景的潜在目标。然而，为了防止删除仍然存在于场景中但由于缺少检测而无法找到匹配的真实正轨迹，我们在确保$T_{unmatch}^q$是消失轨迹$T_{lost}^q$之前，继续跟踪$Ag{e}_{max}$帧的每个不匹配轨迹$T_{unmatch}^q$，其中q∈{1，2，··，m_t−1−w_t}，并将其从关联轨迹集合中删除。理想情况下，我们的3D MOT系统可以在不删除的情况下插入具有缺失检测的真实正轨迹，并且只删除离开场景的轨迹。

4. 新型3D MOT评估工具

  作为开创性的3D MOT基准，KITTI[9]数据集对3D MOT系统的进展至关重要。尽管KITTI数据集提供了3D目标轨迹，但它仅支持2D MOT评估，即图像平面上的评估，并且目前还没有直接在3D空间中评估3D MOT系统的工具。在KITTI数据集上，评估3D MOT系统的当前惯例是将3D跟踪结果投影到图像平面，然后使用KITTI 2D MOT评估工具，该工具使用2D IoU作为成本函数，将投影的跟踪结果与图像平面上的真值轨迹相匹配。然而，我们认为这将阻碍3D MOT系统的未来发展，因为在图像平面上进行评估无法提供3D MOT的公平比较。例如，输出具有错误深度估计和低3D IoU以及真值的3D轨迹的系统仍然可以在2D MOT评估中获得高性能，只要3D轨迹输出在图像平面上的投影与图像平面上的真值具有高2D IoU。

  为了提供3D MOT系统的公平比较，我们对KITTI 2D MOT评估工具进行了扩展，用于3D MOT评估。具体而言，我们将成本函数从2D IoU修改为3D IoU，并将3D跟踪结果与3D空间中的3D真值轨迹直接匹配。这样，我们就不再需要将3D跟踪结果投影到图像平面上进行评估。对于每个被跟踪的目标，其与真值的3D IoU必须高于阈值IoU_thres（或中心距离必须低于阈值Dist_thres），才能被视为成功匹配。虽然我们的3D MOT评估工具的扩展很简单，但我们希望它可以作为评估未来3D MOT系统的标准。

5. 新的MOT评估指标

A. CLEAR指标的限制

  传统的MOT评估基于CLEAR指标[35]，如MOTA（详见第VI-A节）、MOTP、FP、FN、精度、F1得分、IDS、FRAG。然而，这些度量中没有一个明确考虑目标的置信度分数s。换句话说，CLEAR度量考虑具有相同置信度s=1的所有目标轨迹，这是一个不合理的假设，因为可能存在许多具有低置信度分数的假阳性轨迹。因此，为了减少误报的数量并实现较高的MOTA（MOTA是大多数MOT基准中排名的主要指标。），用户必须手动选择阈值，并在提交结果进行评估之前过滤掉置信分数低于阈值的跟踪目标。我们对上述评估的观察结果有两个方面：（1）为3D MOT系统选择最佳阈值需要用户付出不小的努力，如果3D MOT改变其输入检测或在不同的数据集上进行评估，则置信阈值可能会显著不同。因此，用户必须对验证集进行大量实验，以调整置信阈值；（2） 使用单个置信阈值进行评估阻止了我们理解3D MOT系统的性能如何作为阈值的函数而变化。事实上，我们观察到不同的置信阈值会显著影响CLEAR度量的性能。例如，我们使用KITTI MOT数据集的汽车子集的数据，在图3中显示了我们的系统在不同阈值下的三个指标上的性能。为了生成结果，我们首先基于置信度得分s（我们将目标轨迹的置信分数定义为其在所有帧中的置信分数的平均值。）对跟踪结果进行排序。然后，我们定义了一组基于0到1之间的系统召回的置信阈值，间隔为0.025。这导致40个置信阈值，不包括对应于召回0的置信阈值。对于每个置信阈值，我们仅使用置信度高于阈值的轨迹来评估结果。我们表明，在图3（a）中，置信阈值不应该很小（召回率不是很高），因为误报的数量会急剧增加，特别是当召回率达到0.95时。此外，在图3（b）中，置信阈值不应该很大，即召回不应该很小，因为它会导致大量的假阴性。结果，在图3（c）中，我们观察到，只有当我们选择与0.9的召回相对应的置信阈值时，才能获得最高的MOTA值，该阈值平衡了假阳性和假阴性。

  基于上述观察结果，我们认为，使用单一置信阈值进行评估需要用户付出不小的努力，更重要的是，这会妨碍我们理解MOT系统的全方位准确性。一个结果是，一个MOT系统在单个阈值上具有高MOTA，而在其他阈值上具有低MOTA，仍然可以在排行榜上排名靠前。但理想情况下，我们应该致力于开发在多个阈值上实现高MOTA的MOT系统，即在使用不同检测作为输入时实现高性能的3D MOT系统。先前的工作[36]与我们有着相同的精神，因为[36]也认为了解MOT系统在许多操作点的性能非常重要。具体而言，[36]在不同的召回和精度值下计算MOTA矩阵，类似于我们的MOTA-over-recall曲线。区别在于，我们还提出了积分度量（见第V-B节），将多个操作点的性能汇总为单个标量，以便于比较。

图3. （a）（b）（c）置信阈值对CLEAR度量的影响：MOTA、FN和FP。我们使用所提出的3D MOT评估工具在KITTI数据集上评估了我们的3D MOT系统。我们表明，为了实现最高的MOTA，需要选择适当的置信阈值，否则由于大量的假阳性或假阴性，MOTA的性能将显著降低。（d） MOTA中尺度调整的效果：所提出的尺度精度sMOTA在任何召回值下都具有100%的上限。

B. 积分指标：AMOTA和AMOTP

  为了解决当前MOT评估指标不考虑置信度，仅在单个阈值进行评估的问题，我们提出了两个综合指标——AMOTA和AMOTP（平均MOTA和MOTP）——以总结MOTA和MOTP在多个阈值上的表现。AMOTA和AMOTP是通过在所有召回值上整合MOTA和MOTP值来计算的，例如，用于计算AMOTA的MOTA-over-recal曲线下的面积。与其他积分度量（如目标检测中使用的平均精度）类似，我们使用离散召回值集合的总和来近似积分。具体而言，给定[35]中MOTA度量的原始定义：

其中num_gt是所有帧中的真值目标的数量。AMOTA的定义如下：

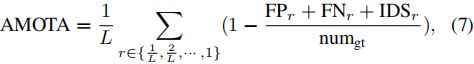
其中FPr、FNr和IDSr是在特定召回值r下计算的假阳性、假阴性和身份切换的数量。此外，L是召回值的数量（积分的置信阈值的数量）。L越高，近似积分就越精确。然而，大L需要在评估期间进行大量计算。为了平衡准确度和速度，我们使用了40个召回值（即，从0%到100%，间隔为2.5%，不包括0%），即L=40。对于最大召回率小于100%的3D MOT系统，超过r_m的集成MOTA值为0。因此，我们提出的指标偏向于高召回率系统。我们认为，这种偏差是可以接受的，因为在实践中，具有高召回率对于防止自动系统的碰撞至关重要。注意，我们提出的AMOTA度量类似于独立工作[37]中提出的PR-MOTA度量。

C. 缩放精度度量：sAMOTA

  传统上，诸如平均精度的积分度量是从0%到100%的百分比，因此很容易测量系统的绝对性能。为了确保积分度量的范围在0%和100%之间，在每个操作点用于计算积分度量的度量也应在0%到100%之间。然而，我们在图3（c）中观察到，在许多召回值下，MOTA可能具有低于100%的严格上限。事实上，特定召回值r下的MOTA上限如下：

第一个不等式是真的，因为假阳性FPr和身份切换IDSr总是非负的。此外，第二个不等式使用了FNr≥num_gt×（1−r）的事实，因为如果召回是r，则意味着至少（1−r）的总目标（num_gt）没有被跟踪。如果r是MOTAr上的上界，则积分度量AMOTA的上界为50%（即，上界r在MOTA vs Recall曲线中创建三角形）。

  为了使积分度量AMOTA的值从0%到100%，我们需要缩放MOTAr的范围。从等式8中，我们发现MOTAr具有严格的r上界的原因是FNr≥num_gt×（1−r）。为了调整MOTAr，我们提出了两个新的度量，称为sMOTA（缩放MOTA）和sAMOTA（缩放AMOTA），其定义如下：

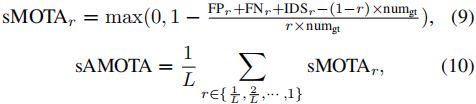
通过从分子中的FNr中减去目标数num_gt×（1−r），所提出的sMOTAr现在上限为100%，导致sAMOTA也上限为100%。注意，我们还在分母中添加了标量因子r，因为我们认为使用召回值为r（即，r×num_gt）时可用的真值目标的实际数量比使用目标总数num_gt更有意义，其中一些甚至在召回值为r时无法跟踪。此外，我们在等式9中添加了一个超过零的最大运算，这是将sMOTAr的下限调整为零。否则，如果存在许多误报或身份切换，sMOTAr可能接近负值。结果，如图3（d）所示，等式9中提出的sMOTAr的范围可以在0%和100%之间，这也导致相应的积分度量sAMOTA的范围在0%到100%之间。总之，我们认为，提出的新积分度量——sAMOTA、AMOTA、AMOTP——能够总结MOT系统在所有阈值上的性能。

6. 实验

A. 设置

评估指标。除了提出的sAMOTA、AMOTA和AMOTP，我们还评估了标准的CLEAR度量，如MOTA、MOTP（多目标跟踪精度）、IDS（身份切换数量）、FRAG（轨迹碎片数量）、FPS（每秒帧数）。

表I. 使用所提出的具有新指标的三维MOT评估工具，在KITTI-VAL集合上对汽车的性能进行评估。

表II. 行人和骑车人在KITTI VAL集合的性能。

表III. NUSCENES VAL集合上所有类别的性能。

数据集。我们对KITTI和nuScenes 3D MOT数据集进行了评估，这些数据集提供了LiDAR点云和3D边界框轨迹。由于KITTI测试集仅支持2D MOT评估，且其真值未向用户发布，因此我们必须使用KITTI val集进行3D MOT评估。此外，我们正在与nuTomony合作，使用我们提出的指标在nuScenes数据集上构建3D MOT评估。然而，第一个nuScenes 3D MOT挑战在本作品开发时尚未完成。因此，我们使用评估工具在nuScenes val集上评估3D MOT系统，以进行临时比较。对于nuScene数据集的未来评估，我们建议用户使用nuScene提供的评估代码，并主要评估nuScene测试集上的3D MOT系统进行比较，尽管我们在val集上开发的临时比较仍然可以用于参考。

  在数据划分方面，我们在KITTI上遵循[16]，使用序列1、6、8、10、12、13、14、15、16、18、19作为val集合，使用其他序列作为train集合，通过我们的3D MOT系统不需要训练。对于nuScene，我们使用其默认数据划分。关于目标类别，我们遵循KITTI惯例，并显示每个类别（汽车、行人、骑车人）的结果。对于nuScene，我们首先获得每个类别的结果，然后通过对7个类别（汽车、卡车、拖车、行人、自行车、摩托车、公共汽车）进行平均来计算最终性能。对于匹配标准，我们遵循KITTI 3D目标检测基准中的惯例，并使用3D IoU来确定成功的匹配。具体来说，我们对行人和骑车人使用0.25，0.5的3D IoU阈值IoU_thres，对汽车使用0.25，0.5，0.7的IoU_thres。在nuScene上，我们遵循nuScene挑战中定义的标准，使用2米的中心距离Dist_thres。

基线。我们与现代开源3D MOT系统（如FANTrack[15]和mmMOT[30]）进行了比较。我们将PointRCNN[6]在KITTI上获得的3D检测和Megvii[34]在nuScenes上获得的相同3D检测用于我们提出的方法和基线[15]，[30]，这些基线需要3D检测作为输入。对于同样需要2D检测作为输入的基线[15]，我们使用3D检测的2D投影。

实施细节。对于表I、III、II和IV中的最佳结果，我们使用（x，y，z，θ，l，w，h，s，v_x，v_y，v_z）作为3D卡尔曼滤波器的状态空间，而不包括角速度v_θ。我们在出生和废弃记录模块中使用F_min=3和Age_min=2。对于数据关联模块中拒绝匹配的阈值，我们根据经验发现，使用IoU_min=0.01（汽车）、Dist_max=1（行人）、Dist_max=6（骑车人）可以在KITTI数据集上获得最佳性能。在nuScenes数据集上，我们对所有目标类别使用Dist_max=10。对于其他详细的超参数，请直接检查我们的代码。

B. 实验结果

KITTI val集上汽车的结果。我们总结了表I中的结果。当使用不同的匹配标准（例如，3D IoU_thres=0.25，0.5和0.7）时，我们提出的3D MOT系统在所有指标上均优于其他现代3D MOT。因此，我们在汽车的KITTI val集上建立了新的最先进3D MOT性能，并实现了令人印象深刻的零身份切换。

行人和骑车人的结果。除了对汽车进行评估外，我们还报告了表II中设置的KITTI val上的行人和骑车人等其他目标的3D MOT性能。尽管由于目标的尺寸较小，跟踪行人和骑车人比跟踪汽车更具挑战性，但我们展示了我们3D MOT系统的强大性能。

nuScenes val集中所有目标的结果。除了对KITTI数据集进行评估外，我们还报告了表III中nuScenes val集的3D MOT结果。我们强调，由于稀疏的LiDAR点云输入、复杂的场景和低帧率，nuScene数据集比KITTI更具挑战性。因此，nuScene上的3D检测质量显著低于KITTI上的3D检测，导致所有3D MOT系统在nuScene中的绝对性能都较低。我们的3D MOT系统在所有指标上仍优于其他3D MOT。

表IV. 使用所提出的具有新指标的3D MOT评估工具对KITTI VAL集合上的汽车进行消融研究。

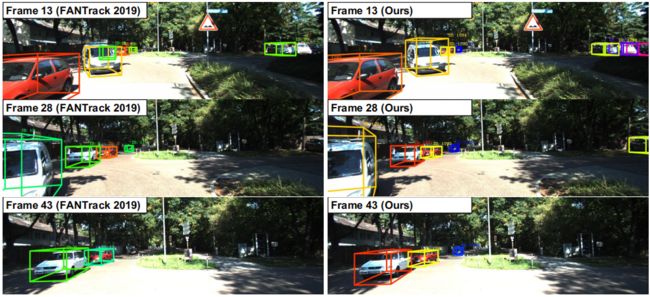
图4. 在KITTI test集的序列3上，FANTrack[15]（左）和我们的系统（右）之间的定性比较。

推理时间。我们比较了表I最后一列中所有方法的推理时间。我们的3D MOT系统（不包括3D检测器部分）在KITTI val集上以207.4 FPS的速度运行，无需GPU，在表I中的其他3D MOT中实现了最快的速度。

定性比较。我们显示了我们的3D MOT系统与[15]和图4之间的定性比较。3D跟踪结果通过彩色3D边界框在图像上可视化，其中颜色表示目标身份。我们可以看到，FANTrack（左）的结果包含一些身份切换和图像最右侧目标的未命中跟踪，而我们的系统（右）在示例序列中没有这些问题。我们在演示视频中提供了3D MOT系统的更多定性结果，这表明（1）我们的系统不需要训练，在数据集上不存在过拟合问题，（2）我们的体系通常产生更稳定的结果，并且具有更少的身份切换和抖动的边界框。

C. 消融研究

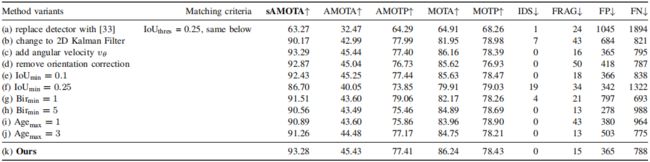
  我们使用提议的3D MOT评估工具以及新的指标对KITTI val集上的汽车进行了所有消融分析，总结见表IV。

3D检测质量的影响。在表IV（a）中，我们将3D检测模块从[6]切换到[33]。区别在于[6]需要LiDAR点云作为输入，而[33]只需要单个图像。结果，单目3D检测器[33]产生的3D检测质量远低于基于LiDAR的3D检测器[6]（详见[6]，[33]）。我们可以看到，（k）中的3D MOT性能也优于（a），这表明3D检测质量对3D MOT系统的性能至关重要。

3D v.s.2D卡尔曼滤波器。我们将最终模型（k）中的3D卡尔曼滤波器替换为（b）中的2D卡尔曼滤波器[19]。具体而言，我们定义了目标轨迹T的状态空间=（x，y，a，r，s，v_x，v_y，v_a），其中（x，y）是目标的2D位置，a是2D框面积，r是纵横比，（v_x，v_y，v_a）表示2D图像平面中的速度。我们观察到，在（k）中使用3D卡尔曼滤波器将IDS从7减少到0，FRAG从43减少到15，我们认为这是因为在3D空间中的跟踪可以帮助解决在2D图像平面中跟踪时存在的深度模糊。总体而言，绝对sAMOTA、AMOTA和MOTA值提高了3%至4%。

角速度v_θ的影响。我们将v_θ添加到状态空间，使得轨迹T的状态空间在表IV（c）中=（x，y，z，θ，l，w，h，s，v_x，v_y，v_z，v_θ）。我们观察到，与（k）相比，添加v_θ使sAMOTA和AMOTA提高了0.01%，AMOTP和MOTA降低了0.08%。这表明，添加角速度或不添加角速度对所有指标的性能都没有明显影响。因此，为了简单起见，我们不将角速度包含在最终系统的状态空间中。

方向修正的影响。如第III-D节所述，我们在表IV（k）中的最终系统中使用了定向校正技术。在这里，我们在不使用表IV（d）中的取向校正的情况下实验了一种变体。我们观察到，方位校正有助于提高所有度量的性能，这表明该技术对我们提出的3D MOT系统有用。

阈值IoU_min的影响。我们将IoU_min=0.01在（k）更改为IoU_min=0.1在（e）和IoU_min=0.25在（f）。我们观察到，增加IoU_min会导致所有指标的持续下降。

Bir_min的影响。我们将Bir_min=3在（k）调整为Bir_min=1在（g）和Bir_min=5在（h）。我们表明，使用Bir_min=1（即，立即为不匹配的检测创建新的轨迹）或Bir_min=5（即，在接下来的五帧中匹配不匹配的检测之后创建新轨迹）导致sAMOTA、AMOTP和MOTA的性能较差，这表明使用Bir_min=3是最好的。

Age_max的影响。我们通过在（i）中将其减小到Age_max=1并在（j）中将其增大到Age_max=3来验证Age_max的效果。我们表明，（i）和（j）都导致了sAMOTA、AMOTA和MOTA的下降，这表明在我们的最终模型（k）中Age_max=2（即在接下来的两帧中保持跟踪不匹配的轨迹T_unmatch）是最佳选择。

7. 结论

  我们提出了一种精确、简单、实时的在线3D MOT系统。此外，还提出了一种新的3D MOT评估工具，以及三种新的度量标准，以标准化未来的3D MOT评估。通过在KITTI和nuScenes 3D MOT数据集上的大量实验，我们的系统建立了最先进的3D MOT性能，同时实现了最快的速度。我们希望，我们的系统将作为一个坚实的基线，其他人可以在其基础上轻松地推进3D MOT的最新技术。

ACKNOWLEDGMENT

This work was funded in part by the Department of Homeland Security award 2017-DN-077-ER0001. Also, we thank the authors of SORT [19], which inspired our work.

REFERENCES

[1] S. Wang, D. Jia, and X. Weng, “Deep Reinforcement Learning for Autonomous Driving,” arXiv:1811.11329, 2018.
[2] X. Weng, J. Wang, S. Levine, K. Kitani, and R. Nick, “Sequential Forecasting of 100,000 Points,” arXiv:2003.08376, 2020.
[3] X. Sun, X. Weng, and K. Kitani, “When We First Met: Visual-Inertial Person Localization for Co-Robot Rendezvous,” arXiv:2006.09959, 2020.
[4] A. Manglik, X. Weng, E. Ohn-bar, and K. M. Kitani, “Forecasting Time-to-Collision from Monocular Video: Feasibility, Dataset, and Challenges,” IROS, 2019.
[5] S. Ren, K. He, R. Girshick, and J. Sun, “Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks,” NIPS, 2015.
[6] S. Shi, X. Wang, and H. Li, “PointRCNN: 3D Object Proposal Generation and Detection from Point Cloud,” CVPR, 2019.
[7] N. Lee, X. Weng, V. N. Boddeti, Y. Zhang, F. Beainy, K. Kitani, and T. Kanade, “Visual Compiler: Synthesizing a Scene-Specific Pedestrian Detector and Pose Estimator,” arXiv:1612.05234, 2016.
[8] X. Weng, S. Wu, F. Beainy, and K. Kitani, “Rotational Rectification Network: Enabling Pedestrian Detection for Mobile Vision,” WACV, 2018.
[9] A. Geiger, P. Lenz, and R. Urtasun, “Are We Ready for Autonomous Driving? the KITTI Vision Benchmark Suite,” CVPR, 2012.
[10] J. H. Yoon, C. R. Lee, M. H. Yang, and K. J. Yoon, “Online MultiObject Tracking via Structural Constraint Event Aggregation,” CVPR, 2016.
[11] H. Karunasekera, H. Wang, and H. Zhang, “Multiple Object Tracking with Attention to Appearance, Structure, Motion and Size,” IEEE Access, 2019.
[12] S. Sharma, J. A. Ansari, J. K. Murthy, and K. M. Krishna, “Beyond Pixels: Leveraging Geometry and Shape Cues for Online Multi-Object Tracking,” ICRA, 2018.
[13] W. Tian, M. Lauer, and L. Chen, “Online Multi-Object Tracking Using Joint Domain Information in Traffic Scenarios,” IEEE Transactions on Intelligent Transportation Systems, 2019.
[14] D. Frossard and R. Urtasun, “End-to-End Learning of Multi-Sensor 3D Tracking by Detection,” ICRA, 2018.
[15] E. Baser, V. Balasubramanian, P. Bhattacharyya, and K. Czarnecki, “FANTrack: 3D Multi-Object Tracking with Feature Association Network,” IV, 2020.
[16] S. Scheidegger, J. Benjaminsson, E. Rosenberg, A. Krishnan, and K. Granstr, “Mono-Camera 3D Multi-Object Tracking Using Deep Learning Detections and PMBM Filtering,” IV, 2018.
[17] R. Kalman, “A New Approach to Linear Filtering and Prediction Problems,” Journal of Basic Engineering, 1960.
[18] H. W Kuhn, “The Hungarian Method for the Assignment Problem,” Naval Research Logistics Quarterly, 1955.
[19] A. Bewley, Z. Ge, L. Ott, F. Ramos, and B. Upcroft, “Simple Online and Realtime Tracking,” ICIP, 2016.
[20] A. Patil, S. Malla, H. Gang, and Y.-T. Chen, “The H3D Dataset for Full-Surround 3D Multi-Object Detection and Tracking in Crowded Urban Scenes,” ICRA, 2019.
[21] L. Zhang, Y. Li, and R. Nevatia, “Global Data Association for MultiObject Tracking Using Network Flows,” CVPR, 2008.
[22] S. Schulter, P. Vernaza, W. Choi, and M. Chandraker, “Deep Network Flow for Multi-Object Tracking,” CVPR, 2017.
[23] X. Weng, Y. Wang, Y. Man, and K. Kitani, “GNN3DMOT: Graph Neural Network for 3D Multi-Object Tracking with 2D-3D MultiFeature Learning,” CVPR, 2020.
[24] H. Pirsiavash, D. Ramanan, and C. C. Fowlkes, “Globally-Optimal Greedy Algorithms for Tracking a Variable Number of Objects,” CVPR, 2011.
[25] W. Choi, “Near-Online Multi-Target Tracking with Aggregated Local Flow Descriptor,” ICCV, 2015.
[26] C. Dicle, O. I. Camps, and M. Sznaier, “The Way They Move: Tracking Multiple Targets with Similar Appearance,” ICCV, 2013.
[27] S. H. Bae and K. J. Yoon, “Robust Online Multi-Object Tracking Based on Tracklet Confidence and Online Discriminative Appearance Learning,” CVPR, 2014.
[28] Y.-J. Li, Z. Luo, X. Weng, and K. Kitani, “Learning Shape Representations for Clothing Variations in Person Re-Identification,” arXiv:2003.07340, 2020.
[29] A. Osep, W. Mehner, M. Mathias, and B. Leibe, “Combined Imageand World-Space Tracking in Traffic Scenes,” ICRA, 2017.
[30] W. Zhang, H. Zhou, S. Sun, Z. Wang, J. Shi, and C. C. Loy, “Robust Multi-Modality Multi-Object Tracking,” ICCV, 2019.
[31] X. Weng, Y. Yuan, and K. Kitani, “Joint 3D Tracking and Forecasting with Graph Neural Network and Diversity Sampling,” arXiv:2003.07847, 2020.
[32] Y. Wang, X. Weng, and K. Kitani, “Joint Detection and Multi-Object Tracking with Graph Neural Networks,” arXiv:2006.13164, 2020.
[33] X. Weng and K. Kitani, “Monocular 3D Object Detection with PseudoLiDAR Point Cloud,” ICCVW, 2019.
[34] B. Zhu, Z. Jiang, X. Zhou, Z. Li, and G. Yu, “Class-Balanced Grouping and Sampling for Point Cloud 3D Object Detection,” CVPR, 2019.
[35] K. Bernardin and R. Stiefelhagen, “Evaluating Multiple Object Tracking Performance: The CLEAR MOT Metrics,” Journal on Image and Video Processing, 2008.
[36] F. Solera, S. Calderara, and R. Cucchiara, “Towards the Evaluation of Reproducible Robustness in Tracking-by-Detection,” AVSS, 2015.
[37] L. Wen, D. Du, Z. Cai, Z. LeI, M.-C. Chang, H. Qi, J. Lim, M.-H.Yang, and S. Lyu, “UA-DETRAC: A New Benchmark and Protocol for Multi-Object Detection and Tracking,” Computer Vision and Image Understanding, 2020.

参考资料

参考文章原文和源代码，走读一遍，大概就清楚了，以下两篇参考也可以了解了解。

参考一
参考二