R语言限制性立方样条回归
前面用了2篇推文,帮大家梳理了从线性拟合到非线性拟合的常用方法,包括多项式回归、分段回归、样条回归、限制性立方样条回归,以及它们之间的区别和联系,详情请看:
-
多项式回归和样条回归1
-
多项式回归和样条回归2
并且上一篇推文已经介绍了R语言实现多项式回归的内容:R语言非线性拟合:多项式回归
今天主要介绍R语言实现立方样条回归。
读过上面几篇推文的朋友想必已经知道了(没看过的建议先看看),样条回归包括很多种,限制性立方样条只是其中一种,更多的大家可以自己了解。
线性的立方样条
演示所用数据还是用上一篇的数据:
rm(list = ls())
x <- 1:100
k <- c(25, 50, 75)
u <- function(x)ifelse(x > 0, x, 0)
x2 <- u(x - k[1])
x3 <- u(x - k[2])
x4 <- u(x - k[3])
set.seed(1)
y <- 0.8 + 1*x + -1.2*x2 + 1.4*x3 + -1.6*x4 + rnorm(100,sd = 2.2)
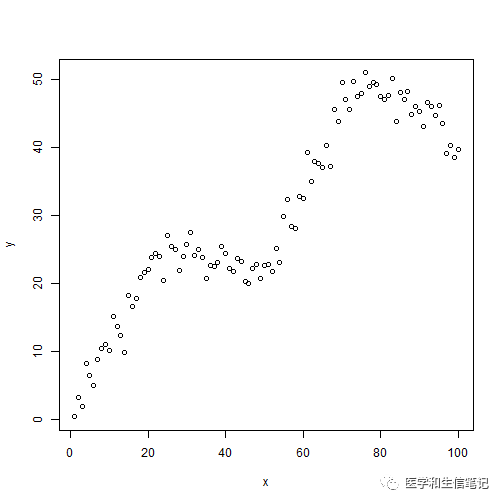
plot(x, y)
假设我们有这样一个数据,很明显这不是一个直线的关系,这时候再用直线回归就不适合了。但是为了演示,这里还是给大家用直线回归方法拟合一下看看效果。
f <- lm(y ~ x)
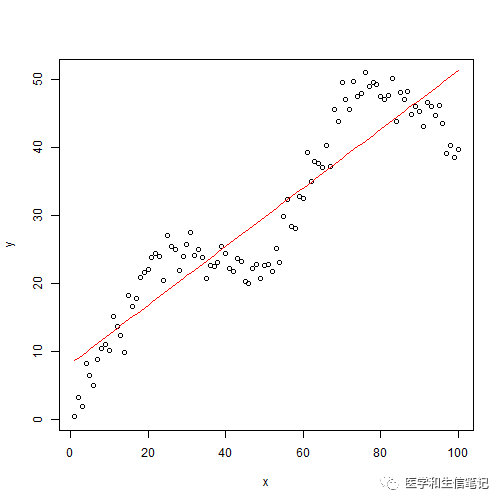
plot(x, y)
lines(x, fitted(f),col="red")
很明显,直线回归是不可能有很好的拟合效果的。这时候我们应该用什么方法拟合这个关系呢?
根据之前的3篇推文,拟合非线性关系有非常多的方法,至少有3种:
-
多项式回归
-
分段回归
-
样条回归
多项式回归在上一篇推文中已经介绍过了,效果不错,但是有一个小小的缺点,在数据两端有上翘趋势,具体可参考之前的推文。
今天给大家演示限制性立方样条回归。做限制性立方样条回归的R包很多,这里以rms为例,以后有机会再介绍其他R包,比如splines。
rms做限制性立方样条回归很简单,对需要使用的变量使用rcs()函数即可。
# 加载R包
library(rms)
# 拟合限制性立方样条,这里对变量x使用,跟多项式回归差不多
f <- lm(y ~ rcs(x,5))
# 画出原数据
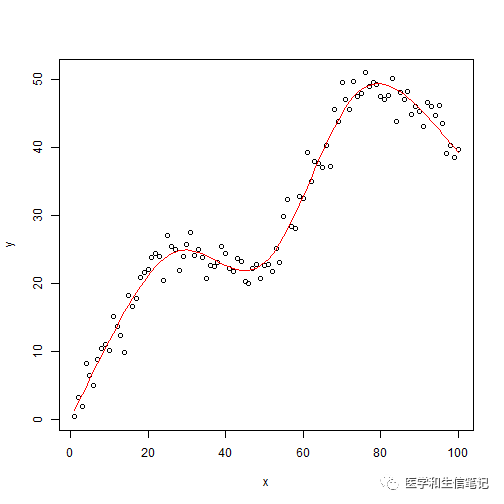
plot(x,y)
lines(x, fitted(f),col="red") # 画出拟合线
可以看到,拟合结果非常完美,甚至比我们的6次多项式拟合还要好一点!
下面解释下上述代码中的意思。rcs是我们的立方样条函数,其中的数字5表示我们要用5个节点(不理解这里的节点啥意思的请去看开头的两篇推文)。
默认节点是4,一般建议选3-6个左右,可以分别试试效果,选择拟合较好的那一个,参考文献是这篇:F. Harrell. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis.
我们可以自己指定,比如根据分位数、中位数、平均数等,都可以作为我们的节点。
下面用ggplot2画图。
df.tmp <- data.frame(x=x,y=y)
ggplot(df.tmp, aes(x,y))+
geom_point(size=2)+
geom_smooth(method = "lm",
formula = y ~ rcs(x,5),
se = T,
color="red"
)+
theme_bw()
此方法同样也是适用于logistic回归和cox回归的,建议使用rms包中的lrm函数和cph进行拟合。
逻辑回归的立方样条
逻辑回归和cox回归就不展开讲了,用法一模一样。
library(rms)
# 逻辑回归数据
getHdata(titanic3)
# 使用rms前先把数据打包
dd <- datadist(titanic3); options(datadist='dd')
# 逻辑回归的立方样条
f <- lrm(survived ~ rcs(sqrt(age),5) + sex, data=titanic3)
f
## Frequencies of Missing Values Due to Each Variable
## survived age sex
## 0 263 0
##
## Logistic Regression Model
##
## lrm(formula = survived ~ rcs(sqrt(age), 5) + sex, data = titanic3)
##
##
## Model Likelihood Discrimination Rank Discrim.
## Ratio Test Indexes Indexes
## Obs 1046 LR chi2 328.06 R2 0.363 C 0.794
## 0 619 d.f. 5 R2(5,1046)0.266 Dxy 0.587
## 1 427 Pr(> chi2) <0.0001 R2(5,758.1)0.347 gamma 0.593
## max |deriv| 2e-07 Brier 0.168 tau-a 0.284
##
## Coef S.E. Wald Z Pr(>|Z|)
## Intercept 3.0936 0.5428 5.70 <0.0001
## age -0.6383 0.1771 -3.60 0.0003
## age' 1.5544 0.6527 2.38 0.0172
## age'' -12.1583 8.8925 -1.37 0.1715
## age''' 15.8326 16.9397 0.93 0.3500
## sex=male -2.4944 0.1549 -16.10 <0.0001
##
构建好逻辑回归模型后,首先可以用anova()函数查看各自变量的统计显著性:
anova(f)
## Wald Statistics Response: survived
##
## Factor Chi-Square d.f. P
## age 14.97 4 0.0048
## Nonlinear 12.65 3 0.0055
## sex 259.17 1 <.0001
## TOTAL 265.88 5 <.0001
age的Nonlinear的P<0.05,可以认为是符合线性的。
下面我们用图形展示年龄和OR值的关系:
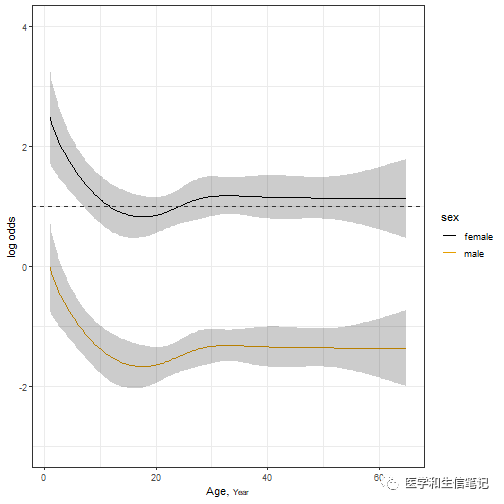
ggplot(Predict(f, age, sex))+ # 加上 fun = plogis 则返回概率
geom_hline(yintercept = 1, color="grey20",linetype=2)+ # OR=1的横线
theme_bw()
unnamed-chunk-18-159921992
纵坐标表示OR值,横坐标是年龄。
cox回归的立方样条
rm(list = ls())
# 构造数据,包括性别(sex),年龄(age),生存时间(time),生存结局(death)
n <- 1000
set.seed(731)
age <- 50 + 12*rnorm(n)
label(age) <- "Age"
sex <- factor(sample(c('Male','Female'), n, rep=TRUE, prob=c(.6, .4)))
cens <- 15*runif(n)
h <- .02*exp(.04*(age-50)+.8*(sex=='Female'))
time<- -log(runif(n))/h
label(time) <- 'Follow-up Time'
death<- ifelse(time <= cens,1,0)
time <- pmin(time, cens)
units(time) <- "Year"
data<-data.frame(age,sex,time,death)
psych::headTail(data)
## age sex time death
## 1 60.58 Male 3.09 1
## 2 42.11 Male 1.57 0
## 3 54.87 Male 3.24 0
## 4 55.82 Male 12.5 0
## ... ... ... ...
## 997 53.02 Female 9.03 0
## 998 38.25 Male 11.72 0
## 999 45.63 Male 12.8 0
## 1000 57.38 Female 3.4 0
使用限制性立方样条进行Cox回归:
# 打包数据
dd <- datadist(data);options(datadist='dd')
# 拟合cox模型
fit<- cph(Surv(time,death) ~ rcs(age,4) + sex,data = data)
fit
## Cox Proportional Hazards Model
##
## cph(formula = Surv(time, death) ~ rcs(age, 4) + sex, data = data)
##
## Model Tests Discrimination
## Indexes
## Obs 1000 LR chi2 78.28 R2 0.083
## Events 183 d.f. 4 R2(4,1000)0.072
## Center -0.2861 Pr(> chi2) 0.0000 R2(4,183)0.334
## Score chi2 83.86 Dxy 0.378
## Pr(> chi2) 0.0000
##
## Coef S.E. Wald Z Pr(>|Z|)
## age -0.0173 0.0286 -0.61 0.5443
## age' 0.2040 0.0767 2.66 0.0079
## age'' -0.7500 0.2679 -2.80 0.0051
## sex=Male -0.6445 0.1488 -4.33 <0.0001
##
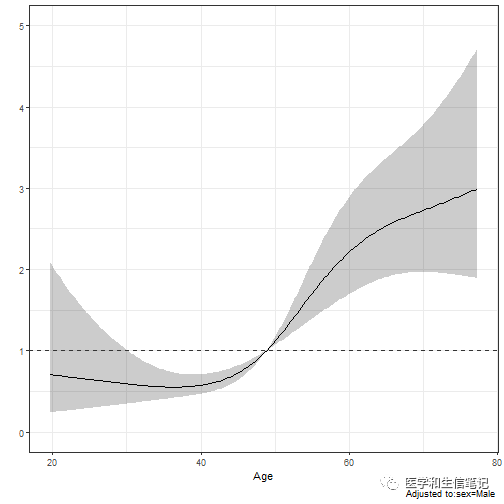
有了这个结果,我们就可以像logistic回归一样,把结果画出来,用来展示年龄和HR值的关系:
ggplot(Predict(fit, age,fun = exp, ref.zero = T))+ # fun = exp,计算HR值,不加这句计算概率
geom_hline(yintercept = 1, color="grey20",linetype=2)+ # HR=1的横线
theme_bw()
通常在文献中还会看到一些竖线,来表示一些比较重要的分割点,比如根据某些值把HR分为大于1和小于1,这样就可以区分在哪一个范围内是保护因素或者风险因素。
我们这个例子,首先可以通过以下函数获取HR=1时的年龄是几岁:
Predict(fit, age,fun = exp, ref.zero = T)
## age sex yhat lower upper
## 1 19.71985 Male 0.7087866 0.2403429 2.0902570
## 2 20.00869 Male 0.7052492 0.2429359 2.0473563
## 。。。。。。略。。。。。。。。
## 96 47.16022 Male 0.8614293 0.8120716 0.9137869
## 97 47.44907 Male 0.8836735 0.8413758 0.9280976
## 98 47.73791 Male 0.9068446 0.8722672 0.9427927
## 99 48.02676 Male 0.9309398 0.9047742 0.9578620
## 100 48.31561 Male 0.9559535 0.9389208 0.9732953
## 101 48.60445 Male 0.9818776 0.9747260 0.9890816
## 102 48.89330 Male 1.0087001 1.0052093 1.0122030
## 103 49.18214 Male 1.0364058 1.0216664 1.0513578
## 104 49.47099 Male 1.0649750 1.0384398 1.0921883
## 105 49.75984 Male 1.0943840 1.0555157 1.1346835
## 106 50.04868 Male 1.1246038 1.0728795 1.1788218
## 107 50.33753 Male 1.1556006 1.0905153 1.2245704
## 108 50.62638 Male 1.1873347 1.1084063 1.2718836
## 109 50.91522 Male 1.2197607 1.1265344 1.3207019
## 110 51.20407 Male 1.2528266 1.1448804 1.3709506
## 111 51.49291 Male 1.2864740 1.1634236 1.4225390
## 。。。。。。略。。。。。。。。
## 200 77.20021 Male 2.9887520 1.8931240 4.7184647
##
## Response variable (y):
##
## Adjust to: sex=Male
##
## Limits are 0.95 confidence limits
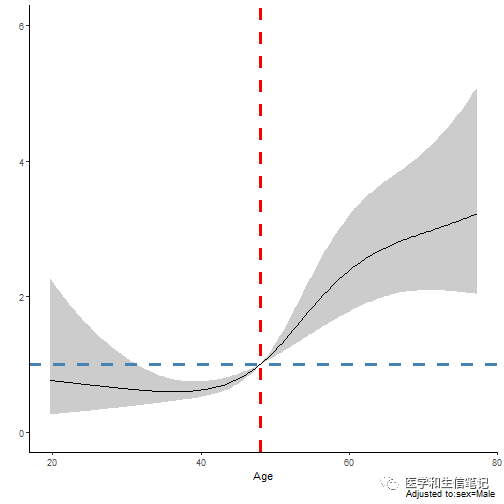
可以看到在第101,102行左右,HR值从0.9变成了1.0,此时对应的年龄大概是48岁,所以我们可以在年龄为48的位置增加一条竖线,以此来区分HR。
dd$limits$age[2] <- 48 # 重新选择HR为1的点
fit <- update(fit) # 更新模型
# 重新画图
ggplot(Predict(fit, age,fun = exp, ref.zero = T))+
geom_hline(yintercept = 1, color="steelblue",linetype=2,size=1.2)+ # HR=1的横线
geom_vline(xintercept = 48, color="red",linetype=2,size=1.2)+
theme_classic()
除此之外,你也可以用返回的数据自己用ggplot2画。
以上就是限制性立方样条回归的演示。欢迎评论区留言或者加入我们的交流群。