CN：Common Neighbor 公共邻居（复杂网络或链路预测等领域）

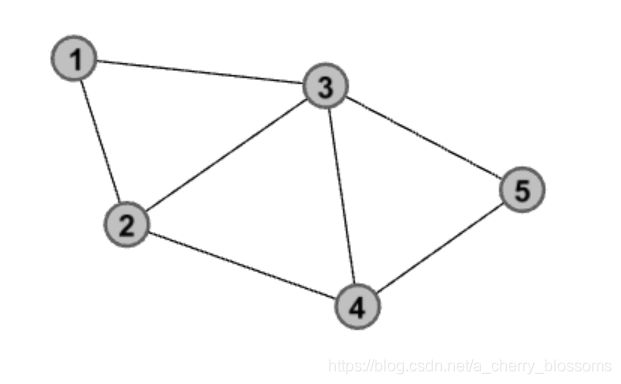
1.给定一个无向图，如下图所示：

这是图形化的表示方式，另外还有其他表现形式：

如边列表（表明哪个节点连接哪个节点，第三列初始化为1，为了计算sim矩阵）：

1	2	1
1	3	1
2	3	1
2	4	1
3	4	1
3	5	1
4	5	1

换句话说就是，比如1 2 1表示的就是节点1和节点2是连接的

如邻接矩阵（有n个节点矩阵的维度就是n*n，且该矩阵是沿对角线对称的，因为它是简单网络所以对角线上的元素为0）：

     0     1     1     0     0
     1     0     1     1     0
     1     1     0     1     1
     0     1     1     0     1
     0     0     1     1     0

换句话说就是，比如第一行第二列的元素值为1，表示节点1和节点2是连接的。

2.公共邻居

公共邻居即CN，Common Neighbor，表示某两个节点都连接到的第三个节点，换句话说就是，如上面那个无向图，和节点1、节点2都连接的节点是不是就是节点3，节点3就称作节点1和节点2的公共邻居；同理，和节点3、节点4都连接的是不是分别有节点2和节点5，则节点2和节点5就称作节点3和节点4的公共邻居。

那么，怎么求一个矩阵中的所有节点对公共邻居的个数呢？有一种笨方法，利用循环，分别遍历每一个节点对，并找到和它们都相连的个数，并统计。

既然有笨方法，是不是还有更高效简便的方法？是的，有，那就是直接让这个邻接矩阵乘以这个邻接矩阵：

我先把实验数据挂上：

环境：可运行的matlab

数据：(1).test.txt

1	2	1
1	3	1
2	3	1
2	4	1
3	4	1
3	5	1
4	5	1

(2).test.m

function [ output_args ] = test( f_name )
%% 读入连边列表linklist，构建网络邻接矩阵net
%文件路径
fpath = ['./undirected_weights/', f_name, '.txt'];

%读取数据得到无向无权网络
linklist = importdata(fpath);
%---- 如果节点编号从0开始，将所有节点编号加1（matlab的下标从1开始）
if ~all(all(linklist(:,1:2)))
    linklist(:,1:2) = linklist(:,1:2)+1;
end

%----对无向图，将第三列元素置为1
linklist(:,3) = 1;
net = spconvert(linklist);
nodenum=length(net);
net(nodenum,nodenum) = 0;                               
% 此处删除自环，对角元为0以保证为方阵
net=net-diag(diag(net));
net = spones(net + net'); 
% 确保邻接矩阵为对称矩阵，即对应于无向网络
disp(net);
f_net =full(net);
disp(f_net);

sim_cn = f_net * f_net;

disp(sim_cn);

end

当我运行这个程序时，sim_cn的值为

     2     1     1     2     1
     1     3     2     1     2
     1     2     4     2     1
     2     1     2     3     1
     1     2     1     1     2

那么，我们就可以照着图验证了（自行验证）。

不想要对角线上的元素可以在sim_cn之后，输出之前加一行

sim_cn(logical(eye(size(sim_cn))))=0;

sim_cn输出为：

     0     1     1     2     1
     1     0     2     1     2
     1     2     0     2     1
     2     1     2     0     1
     1     2     1     1     0

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

这个实际原理是什么呢？我发现：

上面那个图对应的邻接矩阵：A==B

      0     1     1     0     0
      1     0     1     1     0
A     1     1     0     1     1
      0     1     1     0     1
      0     0     1     1     0

      0     1     1     0     0
      1     0     1     1     0
B     1     1     0     1     1
      0     1     1     0     1
      0     0     1     1     0

这个矩阵是关于对角线对称的，那么当A乘以B（注意，这里的矩阵乘法就是行乘以对应列的元素再相加）的时候，即A的行乘以B的列，实际上就等同于A的行乘以A的行，就像

红色的1乘以红色的2就相当于红色的1乘以绿色的3，而这样就会导致结果为0*1+1*0+1*1+0*1+0*0 = 1，即第一行、第二列  ---  节点1、节点2  ---  的公共邻居有1个，且这个公共邻居为节点3（因为结果1是红色1的第三个数和绿色1的第三个数相作用的结果），

按照这种思想，那么你就能口算公共邻居了。比如我们想知道节点3和节点4的公共邻居的个数，找到第三行、第四行（实际上是第四列），两行对应元素相乘再加，得0+1*1+0+0+1*1 = 2，我们到图中验证，发现节点3和节点4得公共邻居有节点2和节点5，刚好就是1*1和1*1作用的结果。

如果我这讲的你们还不理解，最好自己在草稿纸上画一画，算一算，然后你慢慢就会发现这个结果。

3.由CN引出来的基于CN的相似性矩阵。

     0     1     1     2     1
     1     0     2     1     2
     1     2     0     2     1
     2     1     2     0     1
     1     2     1     1     0

这就是基于CN的相似性指标，我们可以在链路预测中看到这样的字眼。上面这个矩阵中对应位置的值越大，则表示为该对节点的相似性越大。这个指标可以用来求出对应的auc和precision等预测值。

4.关于auc和precision，下次接着聊