哈工大机器学习复习笔记(三)
本篇文章是在参考西瓜书、PPT课件、网络上相关博客等资料的基础上整理出的机器学习复习笔记,希望能给大家的机器学习复习提供帮助。这篇笔记只是复习的一个参考,大家一定要结合书本、PPT来进行复习,有些公式的推导最好能够自己演算一遍。由于作者水平有限,笔记中难免有些差错,欢迎大家评论留言。
完整版跳转
8. 支持向量机
8.1 最大间隔方法
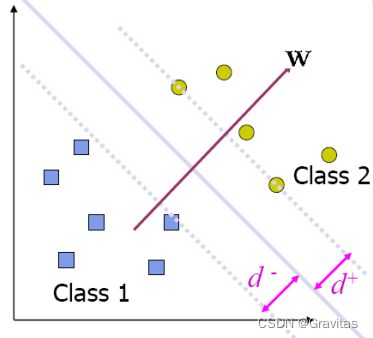
考虑一个二分类问题,当数据集线性可分时,我们想要找到一个平面对数据集进行划分。我们用如下线性方程来描述划分超平面。
w T x + b = 0 w^Tx+b=0 wTx+b=0
其中
w T x i + b > + c for all x i in class 2 w T x i + b < − c for all x i in class 1 w^Tx_i+b>+c \quad \text{for all }x_i \text{ in class 2}\\w^Tx_i+b<-c \quad \text{for all }x_i \text{ in class 1} wTxi+b>+cfor all xi in class 2wTxi+b<−cfor all xi in class 1
可以将上面的两个式子进行合并,得到( y i = ± 1 y_i=\pm1 yi=±1)
( w T x i + b ) y i ≥ c (w^Tx_i+b)y_i \geq c (wTxi+b)yi≥c
两类之间的最小可行间隔(margin)为
m = w T ∣ ∣ w ∣ ∣ ( x i ∗ − x j ∗ ) = 2 c ∣ ∣ w ∣ ∣ m=\frac{w^T}{||w||}(x_{i^*}-x_{j*})=\frac{2c}{||w||} m=∣∣w∣∣wT(xi∗−xj∗)=∣∣w∣∣2c
我们希望这个间隔距离尽可能大,即
max w , b 2 c ∣ ∣ w ∣ ∣ s . t . y i ( w T x i + b ) ≥ c , ∀ i \begin{aligned} \max_{w,b}& \quad \frac{2c}{||w||} \\ s.t. &\quad y_i(w^Tx_i+b)\geq c, \forall i \end{aligned} w,bmaxs.t.∣∣w∣∣2cyi(wTxi+b)≥c,∀i
这就是最大间隔方法。
但是,由于改变 c c c的大小相当于给 w w w和 b b b乘上一个系数,不会改变分类平面,所以可以把优化问题转化为
max w , b 1 ∣ ∣ w ∣ ∣ s . t . y i ( w T x i + b ) ≥ 1 , ∀ i \begin{aligned} \max_{w,b}& \quad \frac{1}{||w||} \\ s.t. &\quad y_i(w^Tx_i+b)\geq 1, \forall i \end{aligned} w,bmaxs.t.∣∣w∣∣1yi(wTxi+b)≥1,∀i
而最大化 ∣ ∣ w ∣ ∣ − 1 ||w||^{-1} ∣∣w∣∣−1等价于最小化 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2,于是上式可重写为
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i + b ) ≥ 1 , ∀ i \begin{aligned} \min_{w,b} & \quad \frac12||w||^2 \\ s.t. & \quad y_i(w^Tx_i+b)\geq 1, \forall i \end{aligned} w,bmins.t.21∣∣w∣∣2yi(wTxi+b)≥1,∀i
这就是支持向量机(SVM)的基本型。
8.2 对偶问题
这个形式的优化问题是凸二次规划问题,已经可以直接求解,但是直接求解的计算复杂度较高。接下来我们会利用拉格朗日对偶性来优化。
数学推导
原问题
min w , b f ( w ) s . t . g i ( w ) ≤ 0 , i = 1 , … , k h i ( w ) = 0 , i = 1 , … , l \begin{aligned} \min_{w,b} & \quad f(w) \\ s.t. &\quad g_i(w)\leq 0, i=1,\dots,k\\ &\quad h_i(w)= 0, i=1,\dots,l\\ \end{aligned} w,bmins.t.f(w)gi(w)≤0,i=1,…,khi(w)=0,i=1,…,l
拉格朗日函数可表示为
L ( w , α , β ) = f ( w ) + ∑ i = 1 k α i g i ( w ) + ∑ i = 1 l β i h i ( w ) L(w,\alpha,\beta)=f(w)+\sum_{i=1}^k\alpha_ig_i(w)+\sum_{i=1}^l\beta_ih_i(w) L(w,α,β)=f(w)+i=1∑kαigi(w)+i=1∑lβihi(w)
其中 α i ≥ 0 , ∀ i \alpha_i \geq 0, \forall i αi≥0,∀i.
引理
max α , β , α i ≥ 0 L ( w , α , β ) = { f ( w ) if w satisfies primal constraints ∞ otherwise \max_{\alpha,\beta,\alpha_i \geq 0}L(w,\alpha,\beta)= \begin{cases} f(w) &\text{if } w \text{ satisfies primal constraints} \\ \infty &\text{otherwise} \end{cases} α,β,αi≥0maxL(w,α,β)={f(w)∞if w satisfies primal constraintsotherwise
原问题可重写为
min w max α , β , α i ≥ 0 L ( w , α , β ) \min_w\max_{\alpha,\beta,\alpha_i \geq 0}L(w,\alpha,\beta) wminα,β,αi≥0maxL(w,α,β)
其对偶问题
max α , β , α i ≥ 0 min w L ( w , α , β ) \max_{\alpha,\beta,\alpha_i \geq 0}\min_wL(w,\alpha,\beta) α,β,αi≥0maxwminL(w,α,β)
弱对偶性
d ∗ = max α , β , α i ≥ 0 min w L ( w , α , β ) ≤ min w max α , β , α i ≥ 0 L ( w , α , β ) = p ∗ d^*=\max_{\alpha,\beta,\alpha_i \geq 0}\min_wL(w,\alpha,\beta)\leq \min_w\max_{\alpha,\beta,\alpha_i \geq 0}L(w,\alpha,\beta)=p^* d∗=α,β,αi≥0maxwminL(w,α,β)≤wminα,β,αi≥0maxL(w,α,β)=p∗
其中对偶问题的最优解为 d ∗ d^* d∗,原问题的最优解为 p ∗ p^* p∗。
强对偶性
there exists a saddle point of L ( w , α , β ) ⟺ d ∗ = p ∗ \text{there exists a saddle point of }L(w,\alpha,\beta) \iff d^*=p^* there exists a saddle point of L(w,α,β)⟺d∗=p∗
KKT条件
如果 L L L中有鞍点,那么鞍点将会满足KKT条件
∂ ∂ w i L ( w , α , β ) = 0 , i = 1 , … , k ∂ ∂ α i L ( w , α , β ) = 0 , i = 1 , … , m ∂ ∂ β i L ( w , α , β ) = 0 , i = 1 , … , l α i g i ( w ) = 0 , i = 1 , … , m g i ( w ) ≤ 0 , i = 1 , … , m α i ≥ 0 , i = 1 , … , m h i ( w ) = 0 , i = 1 , … , l \begin{aligned} \frac{\partial}{\partial w_i}L(w,\alpha,\beta)&=0,\quad i=1,\dots,k\\ \frac{\partial}{\partial \alpha_i}L(w,\alpha,\beta)&=0,\quad i=1,\dots,m\\ \frac{\partial}{\partial \beta_i}L(w,\alpha,\beta)&=0,\quad i=1,\dots,l\\ \alpha_i g_i(w)&=0,\quad i=1,\dots,m\\ g_i(w)&\leq0,\quad i=1,\dots,m\\ \alpha_i&\geq0,\quad i=1,\dots,m\\ h_i(w)&=0, \quad i=1,\dots,l \end{aligned} ∂wi∂L(w,α,β)∂αi∂L(w,α,β)∂βi∂L(w,α,β)αigi(w)gi(w)αihi(w)=0,i=1,…,k=0,i=1,…,m=0,i=1,…,l=0,i=1,…,m≤0,i=1,…,m≥0,i=1,…,m=0,i=1,…,l
定理:如果 w ∗ , α ∗ , β ∗ w^*,\alpha^*,\beta^* w∗,α∗,β∗满足KKT条件,那么对偶问题能获得主问题的最优下界。
应用求解
最大间隔方法中的原问题
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i + b ) ≥ 1 , ∀ i \begin{aligned} \min_{w,b} &\quad \frac12||w||^2 \\ s.t. &\quad y_i(w^Tx_i+b)\geq 1, \forall i\\ \end{aligned} w,bmins.t.21∣∣w∣∣2yi(wTxi+b)≥1,∀i
我们可以把约束写成 1 − y i ( w T x i + b ) ≤ 0 1-y_i(w^Tx_i+b)\leq 0 1−yi(wTxi+b)≤0,发现形式与拉格朗日乘子的约束对应上了。
对应的拉格朗日函数
L ( w , b , α ) = 1 2 w T w + ∑ i α i [ 1 − y i ( w T x i + b ) ] L(w,b,\alpha)=\frac12w^Tw+\sum_i\alpha_i[1-y_i(w^Tx_i+b)] L(w,b,α)=21wTw+i∑αi[1−yi(wTxi+b)]
原问题可写成
min w , b max α i ≥ 0 L ( w , b , α ) \min_{w,b}\max_{\alpha_i \geq 0}L(w,b,\alpha) w,bminαi≥0maxL(w,b,α)
我们来考虑这个式子在什么时候取到最小值。我们发现如果 w , b w,b w,b非法,那么整个式子将会趋于无穷大,因为如果 1 − y i ( w T x i + b ) > 0 1-y_i(w^Tx_i+b)>0 1−yi(wTxi+b)>0,那么在最大化 L L L时,相应的 α i \alpha_i αi就会趋向于正无穷,从而导致整个式子的值趋向于正无穷。因此,整个式子的最小值一定在 w , b w,b w,b合法的时候才能取到,此时 L ( w , b , α ) = 1 2 w T w L(w,b,\alpha)=\frac12w^Tw L(w,b,α)=21wTw,即整个式子的最小值恰好等于 1 2 w T w \frac12w^Tw 21wTw的最小值。通过拉格朗日乘子法,我们成功地将有约束极值改造成了无约束极值。
我们求解它的对偶问题
max α i ≥ 0 min w , b L ( w , b , α ) \max_{\alpha_i \geq 0}\min_{w,b}L(w,b,\alpha) αi≥0maxw,bminL(w,b,α)
首先通过 w , b w,b w,b最小化 L L L.
令 L L L对 w w w和 b b b的偏导为零可得
w = ∑ i = 1 m α i y i x i 0 = ∑ i = 1 m α i y i \begin{aligned} w&=\sum_{i=1}^m\alpha_iy_ix_i\\ 0&=\sum_{i=1}^m\alpha_iy_i \end{aligned} w0=i=1∑mαiyixi=i=1∑mαiyi
代入 L L L中,消去 w w w和 b b b,即
L ( w , b , α ) = 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ( x i T x j ) + ∑ i = 1 m α i − ∑ i = 1 m α i y i ( ∑ j = 1 m α j y j x j T x i + b ) = 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ( x i T x j ) + ∑ i = 1 m α i − ∑ i = 1 m α i y i ( ∑ j = 1 m α j y j x j T ) x i − ∑ i = 1 m α i y i b = ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ( x i T x j ) \begin{aligned} L(w,b,\alpha)&=\frac12\sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_j y_i y_j (x_i^Tx_j)+\sum_{i=1}^m\alpha_i-\sum_{i=1}^m\alpha_iy_i(\sum_{j=1}^m\alpha_j y_j x_j^T x_i+b)\\ &=\frac12\sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_j y_i y_j (x_i^Tx_j)+\sum_{i=1}^m\alpha_i-\sum_{i=1}^m\alpha_iy_i(\sum_{j=1}^m\alpha_j y_j x_j^T) x_i-\sum_{i=1}^m\alpha_iy_ib\\ &=\sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_j y_i y_j (x_i^Tx_j) \end{aligned} L(w,b,α)=21i=1∑mj=1∑mαiαjyiyj(xiTxj)+i=1∑mαi−i=1∑mαiyi(j=1∑mαjyjxjTxi+b)=21i=1∑mj=1∑mαiαjyiyj(xiTxj)+i=1∑mαi−i=1∑mαiyi(j=1∑mαjyjxjT)xi−i=1∑mαiyib=i=1∑mαi−21i=1∑mj=1∑mαiαjyiyj(xiTxj)
对偶问题变为
max α i ≥ 0 ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ( x i T x j ) s . t ∑ i = 1 m α i y i = 0 \begin{aligned} \max_{\alpha_i \geq 0} &\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_j y_i y_j (x_i^Tx_j)\\ s.t & \quad \sum_{i=1}^m\alpha_iy_i=0 \end{aligned} αi≥0maxs.ti=1∑mαi−21i=1∑mj=1∑mαiαjyiyj(xiTxj)i=1∑mαiyi=0
这又是一个二次规划问题,但是比原来那个要好解一些。 求出 α i \alpha_i αi之后,我们利用 w = ∑ i = 1 m α i y i x i w=\sum_{i=1}^m\alpha_iy_ix_i w=∑i=1mαiyixi即可恢复出 w w w.
注意到KKT条件,由于
α i g i ( w ) = 0 , i = 1 , 2 , … , m \alpha_ig_i(w)=0, \quad i=1,2,\dots,m αigi(w)=0,i=1,2,…,m

因此只有少数 α i \alpha_i αi非零,我们称这样的样本为支持向量(Support Vectors)。
实际上,我们只需要 α , b \alpha,b α,b即可分类数据,这是因为
w T z + b = ( ∑ i α i y i x i T z ) + b w^Tz+b=(\sum_i\alpha_i y_i x_i^Tz)+b wTz+b=(i∑αiyixiTz)+b
我们甚至能做得更快,注意到只有支持向量的 α i \alpha_i αi才可以非0,在求和的时候只需要取支持向量就行了,即
y ∗ = s i g n ( ∑ i ∈ S V α i y i ( x i T z ) + b ) y^*=sign(\sum_{i \in SV}\alpha_i y_i (x_i^Tz)+b) y∗=sign(i∈SV∑αiyi(xiTz)+b)
8.3 软间隔
在实际应用中,我们的数据可能实际上是线性可分的,但是由于噪声的存在,使得两类的个别数据点之间的距离较近,导致类别之间的距离较近,而如果在这个条件下仍然按照上面的办法求解,显然求得的结果是不合理的(过拟合),甚至有可能出现一类的某个数据点出现在了对侧中,导致不存在分类超平面。因此,我们需要一种手段来使得分类超平面能够容忍这些“错误”的数据点的存在,即允许有些点可以不满足约束
y i ( w T x i + b ) ≥ 1 y_i(w^Tx_i+b) \geq 1 yi(wTxi+b)≥1
当然,在最大化间隔的同时,不满足约束的样本应该尽可能少。于是,优化目标可写为
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m l 0 / 1 ( y i ( w T x i + b ) − 1 ) \min_{w,b} \frac12||w||^2+C\sum_{i=1}^ml_{0/1}(y_i(w^Tx_i+b) -1) w,bmin21∣∣w∣∣2+Ci=1∑ml0/1(yi(wTxi+b)−1)
其中 C > 0 C>0 C>0是一个常数, l 0 / 1 l_{0/1} l0/1是“0/1损失函数”
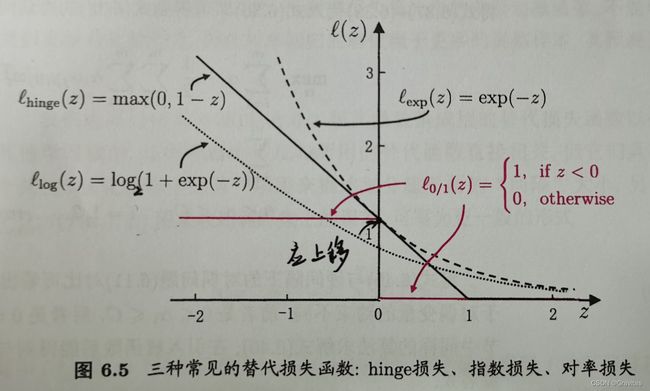
l 0 / 1 ( z ) = { 1 if z < 0 0 otherwise l_{0/1}(z)=\begin{cases} 1 &\text{if } z<0 \\ 0 &\text{otherwise} \end{cases} l0/1(z)={10if z<0otherwise
显然,当 C C C为无穷大时,上式会迫使所有样本均满足约束条件,这实际上就是“硬间隔”;当 C C C取有限值时,上式允许一些样本不满足约束。
然而, l 0 / 1 l_{0/1} l0/1非凸、非连续,数学性质不好,我们通常用一些替代损失函数来替代 l 0 / 1 l_{0/1} l0/1,它们通常是凸的连续函数且是 l 0 / 1 l_{0/1} l0/1的上界。
通常有三种常用的替代损失函数:
- hinge损失: l h i n g l e ( z ) = max ( 0 , 1 − z ) l_{hingle}(z)=\max(0,1-z) lhingle(z)=max(0,1−z)
- 指数损失: l e x p ( z ) = exp ( − z ) l_{exp}(z)=\exp(-z) lexp(z)=exp(−z)
- 对率损失: l l o g ( z ) = log 2 ( 1 + e x p ( − z ) ) l_{log}(z)=\log_2(1+exp(-z)) llog(z)=log2(1+exp(−z))
引入松弛变量 ξ i ≥ 0 \xi_i \geq 0 ξi≥0,优化目标可重写为
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ξ i s . t . y i ( w T x i + b ) ≥ 1 − ξ i , ξ i ≥ 0 , i = 1 , 2 , … , m . \begin{aligned} \min_{w,b} &\quad \frac12||w||^2+C\sum_{i=1}^m\xi_i\\ s.t. & \quad y_i(w^Tx_i+b) \geq 1-\xi_i,\\ & \quad \xi_i \geq 0, \ i=1,2,\dots,m. \end{aligned} w,bmins.t.21∣∣w∣∣2+Ci=1∑mξiyi(wTxi+b)≥1−ξi,ξi≥0, i=1,2,…,m.
特别地,如果样本 x i x_i xi没有误差,则有 ξ i = 0 \xi_i=0 ξi=0, ξ i \xi_i ξi是误差的上界。 C C C称为惩罚系数,是间隔和分类误差之间的“trade-off”。
对偶后的问题变为
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ( x i T x j ) s . t . 0 ≤ α i ≤ C , ∑ i = 1 m α i y i = 0 , i = 1 , 2 , … , m . \begin{aligned} \max_{\alpha} &\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_j y_i y_j (x_i^Tx_j)\\ s.t. & \quad 0\leq \alpha_i \leq C,\\ & \quad \sum_{i=1}^m\alpha_i y_i=0, \ i=1,2,\dots,m. \end{aligned} αmaxs.t.i=1∑mαi−21i=1∑mj=1∑mαiαjyiyj(xiTxj)0≤αi≤C,i=1∑mαiyi=0, i=1,2,…,m.
8.4 核方法
以上的求解都是在线性可分的条件下进行的,而事实上大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。对这样的问题可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。幸运的是,如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。
回顾之前的过程:我们优化对偶问题的时候,并不需要真正地给向量做特征变换,而只需要知道特征变换之后向量的内积;在分类的时候,也只需要向量的内积。所以我们可以这样做:并不显式地升维变量,而是在向量需要求内积的时候,用我们新的函数来替换内积函数。这就是核函数。
所以我们通过核函数,避免了真正执行升维,只需要在计算内积的时候采用核函数来替代。
常用的核函数有:
- 线性核 κ ( x i , x j ) = x i T x j \kappa(x_i,x_j)=x_i^Tx_j κ(xi,xj)=xiTxj,它就是内积,写成这样是为了把采用核函数、不采用核函数的SVM形式统一起来;
- 多项式核 κ ( x i , x j ) = ( 1 + x i T x j ) p \kappa(x_i,x_j)=(1+x_i^Tx_j)^p κ(xi,xj)=(1+xiTxj)p,其中 p p p决定了特征变换之后的维度;
- 径向基 κ ( x i , x j ) = exp ( − 1 2 ∣ ∣ x i − x j ∣ ∣ 2 ) \kappa(x_i,x_j)=\exp(-\frac12||x_i-x_j||^2) κ(xi,xj)=exp(−21∣∣xi−xj∣∣2);
- 高斯核 κ ( x i , x j ) = exp ( − ∣ ∣ x i − x j ∣ ∣ 2 2 σ 2 ) \kappa(x_i,x_j)=\exp(-\frac{||x_i-x_j||^2}{2\sigma^2}) κ(xi,xj)=exp(−2σ2∣∣xi−xj∣∣2) ,它的特征变换之后的维度是无穷大。
哈工大机器学习复习笔记(一)
哈工大机器学习复习笔记(二)
哈工大机器学习复习笔记(三)
哈工大机器学习复习笔记(四)