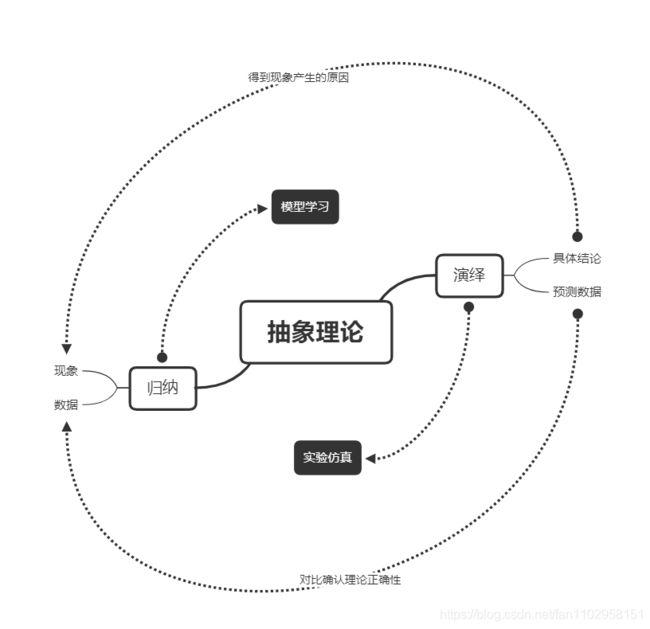
机器学习基础概念（三）：归纳与演绎

引言

子曰：“举一隅，不以三隅返，则不复也”

可是为什么可以从“一隅”得到“三隅”，而我们又该如何从“一隅”得到“三隅”呢？

这就需要追溯到人认识世界的方式上，此处不展开讨论，总结这上亿年的生命演化流程，人类进化出丰富感觉器官感知世界，强壮的大脑处理感受到的信息，最后对相应的信息做出反馈。最初级的反馈是本能的，如膝跳反射，如瞳孔缩放这是不需要后天学习的，是大脑神经系统与生俱来的，是人类的本能；而一些高级的反馈行动则是需要人们通过后天学习去构建从信息输入到行动输出的心智模式来完成。换句话说，别人向你“举一隅”，你需要通过反复认识，深入理解在脑子中构建出“一隅”这个概念——这个就是归纳，它是指从具体示例中抽象出普遍规律的过程。

那么，我们得到了“一隅”之后，又该如何返回“三隅”呢。普遍规律通常是抽象的，因为只有足够抽象才能普适所有的具体情况。那么，仅靠“一隅”这个抽象概念，我们按照“一隅"的普遍规律是无法直接返回”三隅“这个具体情况的。真实的情况是，我们从”一隅“的抽象概念出发推导出”三隅“的抽象概念，再结合实验验证”三隅“概念的正确性，最后才返回三隅。其中从”一隅“这个概念出发得到”三隅“实际的过程就是演绎。

归纳

定义

归纳推理是一种由个别到一般的推理。由一定程度的关于个别事物的观点过渡到范围较大的观点，由特殊具体的事例推导出一般原理、原则的解释方法。自然界和社会中的一般，都存在于个别、特殊之中，并通过个别而存在。一般都存在于具体的对象和现象之中，因此，只有通过认识个别，才能认识一般。人们在解释一个较大事物时，从个别、特殊的事物总结、概括出各种各样的带有一般性的原理或原则，然后才可能从这些原理、原则出发，再得出关于个别事物的结论。这种认识秩序贯穿于人们的解释活动中，不断从个别上升到一般，即从对个别事物的认识上升到对事物的一般规律性的认识。例如，根据各个地区、各个历史时期生产力不发展所导致的社会生活面貌落后，可以得出结论说，生产力发展是社会进步的动力，这正是从对于个别事物的研究得出一般性结论的推理过程，即归纳推理。显然，归纳推理是从认识研究个别事物到总结、概括一般性规律的推断过程。

方式

例如：在一个平面内，直角三角形内角和是180度；锐角三角形内角和是180度；钝角三角形内角和是180度；直角三角形，锐角三角形和钝角三角形是全部的三角形；所以，平面内的一切三角形内角和都是180度。

这个例子从直角三角形，锐角三角形和钝角三角形内角和分别都是180度这些个别性知识，推出了“一切三角形内角和都是180度“这样的一般性结论，就属于归纳推理。

传统上，根据前提所考察对象范围的不同，把归纳推理分为完全归纳推理和不完全归纳推理。完全归纳推理考察了某类事物的全部对象，不完全归纳推理则仅仅考察了某类事物的部分对象。并进一步根据前提是否揭示对象与其属性间的因果联系，把不完全归纳推理分为简单枚举归纳推理和科学归纳推理。

现代归纳逻辑则主要研究概率推理和统计推理。归纳推理的前提是其结论的必要条件。

其次，归纳推理的前提是真实的，但结论却未必真实，而可能为假。如根据某天有一只兔子撞到树上死了，推出每天都会有兔子撞到树上死掉，这一结论很可能为假，除非一些很特殊的情况发生，比如地理环境中发生了什么异常使得兔子必以撞树为快。

我们可以用归纳强度来说明归纳推理中前提对结论的支持度。支持度小于50%的，则称该推理是归纳弱的；支持度小于100%但大于50%的，称该推理是归纳强的；归纳推理中只有完全归纳推理前提对结论的支持度达到100%，支持度达到100%的是必然性支持。

归纳推理的数理逻辑通用演算形式为：s1⊆p+s2⊆p+s3⊆p+〈n〉（s⊆p）=∀×（s⊆p）。

演绎

定义

所谓演绎推理，就是从一般性的前提出发，通过推导即“演绎”，得出具体陈述或个别结论的过程。关于演绎推理，还存在以下几种定义：

①演绎推理是从一般到特殊的推理；

②它是前提蕴涵结论的推理；

③它是前提和结论之间具有必然联系的推理。

④演绎推理就是前提与结论之间具有充分条件或充分必要条件联系的必然性推理。

演绎推理的逻辑形式对于理性的重要意义在于，它对人的思维保持严密性、一贯性有着不可替代的校正作用。这是因为演绎推理保证推理有效的根据并不在于它的内容，而在于它的形式。演绎推理的最典型、最重要的应用，通常存在于逻辑和数学证明中。

方式

三段论

是由两个含有一个共同项的性质判断作前提，得出一个新的性质判断为结论的演绎推理。三段论是演绎推理的一般模式，包含三个部分：大前提——已知的一般原理，小前提——所研究的特殊情况，结论——根据一般原理，对特殊情况作出判断。

例如：知识分子都是应该受到尊重的，人民教师都是知识分子，所以，人民教师都是应该受到尊重的。

其中，结论中的主项叫做小项，用“S”表示，如上例中的“人民教师”；结论中的谓项叫做大项，用“P”表示，如上例中的“应该受到尊重”；两个前提中共有的项叫做中项，用“M”表示，如上例中的“知识分子”。在三段论中，含有大项的前提叫大前提，如上例中的“知识分子都是应该受到尊重的”；含有小项的前提叫小前提，如上例中的“人民教师是知识分子”。三段论推理是根据两个前提所表明的中项M与大项P和小项S之间的关系，通过中项M的媒介作用，从而推导出确定小项S与大项P之间关系的结论 [2]  。

假言推理

是以假言判断为前提的推理。假言推理分为充分条件假言推理和必要条件假言推理两种。

（1）充分条件假言推理的基本原则是：小前提肯定大前提的前件，结论就肯定大前提的后件；小前提否定大前提的后件，结论就否定大前提的前件。如下面的两个例子：

①如果一个数的末位是0，那么这个数能被5整除；这个数的末位是0，所以这个数能被5整除；②如果一个图形是正方形，那么它的四边相等；这个图形四边不相等，所以，它不是正方形。

两个例子中的大前提都是一个假言判断，所以这种推理尽管与三段论有相似的地方，但它不是三段论。

（2）必要条件假言推理的基本原则是：小前提肯定大前提的后件，结论就要肯定大前提的前件；小前提否定大前提的前件，结论就要否定大前提的后件。如下面的两个例子：

①只有肥料足，菜才长得好。这块地的菜长得好，所以，这块地肥料足。②育种时，只有达到一定的温度，种子才能发芽。这次育种没有达到一定的温度，所以种子没有发芽。

选言推理

是以选言判断为前提的推理。选言推理分为相容的选言推理和不相容的选言推理两种。

（1）相容的选言推理的基本原则是：大前提是一个相容的选言判断，小前提否定了其中一个（或一部分）选言支，结论就要肯定剩下的一个选言支。

例如：这个三段论的错误，或者是前提不正确，或者是推理不符合规则；这个三段论的前提是正确的，所以，这个三段论的错误是推理不符合规则。

（2）不相容的选言推理的基本原则是：大前提是个不相容的选言判断，小前提肯定其中的一个选言支，结论则否定其它选言支；小前提否定除其中一个以外的选言支，结论则肯定剩下的那个选言支。例如下面的两个例子：

①一个词，要么是褒义的、要么是贬义的，要么是中性的。“结果”是个中性词，所以，“结果”不是褒义词，也不是贬义词。②一个三角形，要么是锐角三角形，要么是钝角三角形，要么是直角三角形。这个三角形不是锐角三角形和直角三角形，所以，它是个钝角三角形。

关系推理

关系推理是前提中至少有一个是关系命题的推理。

下面简单举例说明几种常用的关系推理：

（1）对称性关系推理，如1米=100厘米，所以100厘米=1米；

（2）反对称性关系推理，a大于b，所以b小于a ；

（3）传递性关系推理，a>b，b>c，所以a>c。

归纳与演绎的区别与联系

归纳和演绎这两种方法既互相区别、互相对立，又互相联系、互相补充，它们相互之间的辩证关系表现为：一方面，归纳是演绎的基础，没有归纳就没有演绎；另一方面，演绎是归纳的前导，没有演绎也就没有归纳。一切科学的真理都是归纳和演绎辩证统一的产物，离开演绎的归纳和离开归纳的演绎，都不能达到科学的真理。

归纳是演绎的基础。演绎是从归纳结束的地方开始的，演绎的一般知识来源于经验归纳的结果。没有大量的机械运动的经验事实，不可能建立能量守恒定律；没有大量的生物杂交的试验事实，不可能创立遗传基因学说。数学是一门演绎成分起重要作用的科学，表面上看似乎不需要经验和归纳，其实不然，数学必须借助于归纳的思维方法才能得到建立和发展。例如，关于素数有这样一条定理：存任一系数和它的二倍之间，至少存在另一个素数。如在2与4之间，有素数3；在3与6之间有素数5；在5与10之间有素数7，等等。显然，素数的这条定理是通过归纳推理得到的。数学的定义、原则、公理等抽象概念，都是归纳人类实践经验的产物，都可以在现实世界找到它们的原型。可见，归纳为演绎准备前提，演绎中包含有归纳，一刻也离不开归纳。

演绎是归纳的前导。归纳虽然是演绎的基础，但归纳本身也离不开演绎的指导，对实际材料进行归纳的指导思想往往是演绎的成果。例如，达尔文的进化论是经过调查和实验，在积累了大量经验材料的基础上，归纳总结出来的结论。但他在作出进化论的结论之前，早就接受了拉马克、赖尔等人的进化论观点，特别是遵循了赖尔的地质演化学说。根据这个理论，当然可以推出地球上生物的物种也是历史地、逐渐地改变的，并非结论从来如此的。因此，达尔文以赖尔的理论作为自己在归纳研究时的指导，从而从大量的生物资料中，概括括出生物进化的科学理论。可见，没有演绎证明了的理论归纳就缺乏明确的目的与指导，因而，归纳一刻也离不开演绎。

归纳和演绎是互为条件，互相渗透，并在一定条件了互相转化。归纳出来的结论，成为演绎的前提，归纳转化为演绎；以一般原理为指导，通过对大量材料的归纳得出一般结论，演绎又转化为归纳。归纳和演绎是相互补充，交替进行。归纳后随之进行演绎，为归纳出的认识成果得到扩大和加深；演绎后随之进行归纳，用对实际材料的归纳来验证和丰富演绎出的结论。人们的认识，在这种交互作用的过程中，从个别到一般，又从一般到个别，循环住复，步步深化。

在逻辑史上，归纳和演绎常常被人们看作是两种不相容的思维形式，看不到二者之间的辩证统一，出现过片面夸大演绎作用“全演绎派”和片面夸大归纳作用的“全归纳派”。从一个级端走向另一个极端，都是牺牲一个而把另一个捧上了天。我们在运用归纳和演绎方法时，必须把二者有机地联系在一起，同时还必须有机地将归纳和演绎的方法与分析和综合等思维方法结合起来运用才能充分发挥逻辑思维的作用。

总结