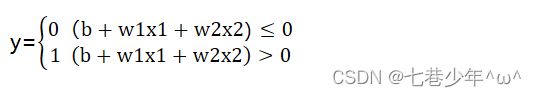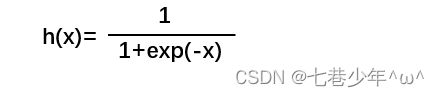第二章.神经网络—激活函数
第二章.神经网络
感知机存在如何设置合适的权重问题,神经网络的出现就是为了解决感知机存在的问题,神经网络的一个重要性质:它可以自动的从数据中学习到合适的权重参数。
2.1.从感知机到神经网络
1.神经网络示例
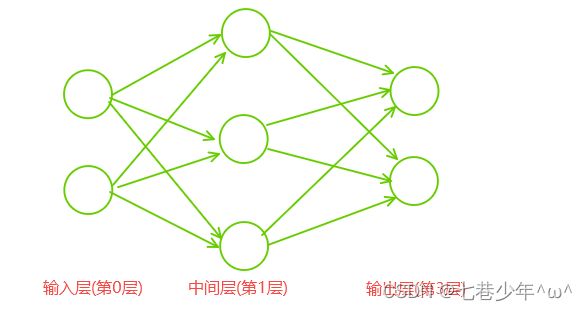
1).示意图:
- 网络一共由3层神经元构成,但是实际上只有两层神经元有权重,因此称为“2层网络”,有的书也会根据构成网络的层数来定义,称为“3层网络”。
2).感知机与激活函数的关联:
①.感知机数学公式:
③.刚才使用的h(x)函数就会将输入信号的总和转换为输出信号,这种函数一般称为激活函数 (作用:在于决定如何来激活输入信号的总和)
2.2.激活函数
1.阶跃函数
1).函数:
2).图像
3).实现:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文乱码
plt.rcParams['axes.unicode_minus'] = False # 解决负号不显示的问题
# 阶跃函数的实现
def sign(x):
return np.array(x > 0, dtype=int)
x_data = np.arange(-5.0, 5.0, 0.1)
y_data = sign(x_data)
plt.figure(figsize=(6, 4))
plt.plot(x_data, y_data, 'r')
plt.ylim(-0.1, 1.1)
plt.title('阶跃函数')
plt.show()
2.Sigmoid函数
1).函数:
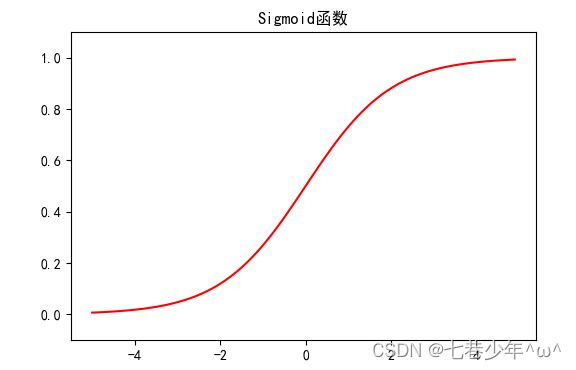
2).图像
3).实现:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文乱码
plt.rcParams['axes.unicode_minus'] = False # 解决负号不显示的问题
# Sigmoid函数的实现
def Sigmoid(x):
return 1 / (1 + np.exp(-x))
x_data = np.arange(-5.0, 5.0, 0.1)
y_data = Sigmoid(x_data)
plt.figure(figsize=(6, 4))
plt.plot(x_data, y_data, 'r')
plt.ylim(-0.1, 1.1)
plt.title('Sigmoid函数')
plt.show()
3.阶跃函数与Sigmoid函数的比较
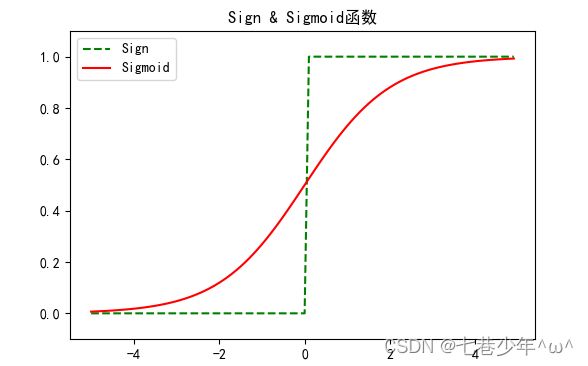
1).图像示意图:
2).图像描述:
①.平滑度不同:阶跃函数是急剧变化的,Sigmoid函数是连续性变化的
②.返回值不同:阶跃函数只能返回0或1,Sigmoid函数返回与函数相关的一系列实数
4.ReLU函数
1).函数:
2).图像
3).实现:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文乱码
plt.rcParams['axes.unicode_minus'] = False # 解决负号不显示的问题
# ReLU函数的实现
def ReLU(x):
return np.maximum(0, x)
x_data = np.arange(-5.0, 5.0, 0.1)
y_data2 = ReLU(x_data)
plt.figure(figsize=(6, 4))
plt.plot(x_data, y_data2, 'r')
plt.title('ReLU函数')
plt.show()