吴恩达《深度学习专项》笔记+代码实战（二）：简单的神经网络——逻辑回归

这堂课要学习的是逻辑回归——一种求解二分类任务的算法。同时，这堂课会补充实现逻辑回归必备的数学知识、编程知识。学完这堂课后，同学们应该能够用Python实现一个简单的小猫辨别器。

前排提示：本文篇幅较长。如果想看本文的精简版，欢迎移步我在其他地方发的文章.

学习提示

如上图所示，深度学习和编程，本来就是相对独立的两块知识。

深度学习本身的知识包括数学原理和实验经验这两部分。深度学习最早来自于数学中的优化问题。随着其结构的复杂化，很多时候我们解释不清为什么某个模型性能更高，只能通过重复实验来验证模型的有效性。因此，深度学习很多情况下变成了一门“实验科学”。

深度学习中，只有少量和编程有关系的知识，比如向量化计算、自动求导器等。得益于活跃的开源社区，只要熟悉了这些少量的编程技巧，人人都可以完成简单的深度学习项目。但是，真正想要搭建一个实用的深度学习项目，需要完成大量“底层”的编程工作，要求开发者有着广泛的编程经验。

通过上吴恩达老师的课，我们应该能比较好地掌握深度学习的数学原理，并且了解深度学习中少量的编程知识。而广泛的编程经验、修改模型的经验，这些都是只上这门课学不到的。

获取修改模型的经验这项任务过于复杂，不太可能短期学会，几乎可以作为研究生的课题了。而相对而言，编程的经验就很好获得了。

我的系列笔记会补充很多编程实战项目，希望读者能够通过完成类似的编程项目，在学习课内知识之余，提升广义上的编程能力。比如在这周的课程里，我们会用课堂里学到的逻辑回归从头搭建一个分类器。

课堂笔记

本节课的目标

在这节课里，我们要完成一个二分类任务。所谓二分类任务，就是给一个问题，然后给出一个“是”或“否”的回答。比如给出一张照片，问照片里是否有一只猫。

这节课中，我们用到的方法是逻辑回归。逻辑回归可以看成是一个非常简单的神经网络。

符号标记

从这节课开始，我们会用到一套统一的符号标记：

$(x,y)$ 是一个训练样本。其中，$x$ 是一个长度为 $n_x$ 的一维向量，即 $x\in {\mathcal{R}}^{n_x}$。$y$ 是一个实数，取0或1，即$y\in \{0,1\}$。取0表示问题的的答案为“否”，取1表示问题的答案为“是”。

这套课默认读者对统计机器学习有基本的认识，似乎没有过多介绍训练集是什么。在有监督统计机器学习中，会给出训练数据。训练数据中的每一条训练样本包含一个“问题”和“问题的答案”。神经网络根据输入的问题给出一个自己的解答，再和正确的答案对比，通过这样一个“学习”的过程来优化解答能力。

对计算机知识有所了解的人会知道，在计算机中，颜色主要是通过RGB（红绿蓝）三种颜色通道表示。每一种通道一般用长度8位的整数表示，即用一个0~255的数表示某颜色在红、绿、蓝上的深浅程度。这样，一个颜色就可以用一个长度为3的向量表示。一幅图像，其实就是许多颜色的集合，即许多长度为3的向量的集合。颜色通道，再算上某颜色所在像素的位置$(x,y)$，图像就可以看成一个3维张量$I\in {\mathcal{R}}^{H\times W\times 3}$，其中$H$是图像高度，$W$是图像宽度，$3$是图像的通道数。在把图像输入逻辑回归时，我们会把图像“拉直”成一个一维向量。这个向量就是前面提到的网络输入$x$，其中$x$的长度$n_x$满足$n_x=H\times W\times 3$。这里的“拉直”操作就是把张量里的数据按照顺序一个一个填入新的一维向量中。

其实向量就是一维的，但我还是很喜欢强调它是“一维”的。这是因为在计算机中所有数据都可以看成是数组（甚至C++的数组就叫vector)。二维数组不过是一维数组的数组，三位数组不过是二维数组的数组。在数学中，为了方便称呼，把一维数组叫“向量”，二维数组叫“矩阵”，三维及以上数组叫“张量”。其实在我看来它们之间只是一个维度的差别而已，叫“三维向量”、“一维张量”这种不是那么严谨的称呼也没什么问题。

实际上，我们有很多个训练样本。样本总数记为$m$。第$i$个训练样本叫做$(x^{(i)},y^{(i)})$。在后面使用其他标记时，也会使用上标$(i)$表示第$i$个训练样本得到的计算结果。

所有输入数据的集合构成一个矩阵（其中每个输入样本用列向量的形式表示，这是为了方便计算机的计算）：

$$X=\left[\begin{array}{cccc}|& |& & |\\ x^{(1)}& x^{(2)}& ...& x^{(m)}\\ |& |& & |\end{array}\right],X\in {\mathcal{R}}^{n_x\times m}$$

同理，所有真值也构成集合 $Y$:

$$Y=\left[\begin{array}{cccc}{y}^{(1)}& y^{(2)}& ...& y^{(m)}\end{array}\right],Y\in {\mathcal{R}}^m$$
由于每个样本$y^{(i)}$是一个实数，所以集合$Y$是一个向量。

逻辑回归的公式描述

逻辑回归是一个学习算法，用于对真值只有0或1的“逻辑”问题进行建模。给定输入$x$,逻辑回归输出一个$\hat{y}$。这个$\hat{y}$是对真值$y$的一个估计，准确来说，它描述的是$y=1$的概率，即$\hat{y}=P(y=1|x)$

逻辑回归会使用一个带参数的函数计算$\hat{y}$。这里的参数包括$w\in {\mathcal{R}}^{n_x},b\in \mathcal{R}$。

说起用于拟合的函数，最容易想到的是线性函数$w^{T}x+b$（即做点乘再加$b$： $w^{T}x+b=({\Sigma }_{i=1}^{n_x}{w}_i{x}_i)+b$ ）。但线性函数的值域是$(-\infty ,+\infty )$（即全体实数$\mathcal{R}$），概率的取值是$[0,1]$。我们还需要一个定义域为$\mathcal{R}$，值域为$[0,1]$，把线性函数映射到$[0,1]$上的一个函数。

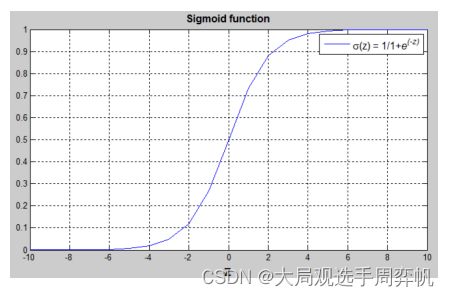
逻辑回归中，使用的映射函数是sigmoid函数$\sigma$,它的定义为：
$$\sigma (z)=\frac{1}{1+e^{-z}}$$

这个函数可以有效地完成映射，它的函数图像长这个样子：

这里不用计较为什么使用这个函数，只需要知道这个函数的趋势：$x$越小，$\sigma (x)$越靠近0；$x$越大，$\sigma (x)$越靠近1。

也就是说，最终的逻辑回归公式长这个样子：$\hat{y}=\sigma (w^{T}x+b)$。

逻辑回归的损失函数（Cost Function）

所有的机器学习问题本质上是一个优化问题，一般我们会定义一个损失函数（Cost Function），再通过优化参数来最小化这个损失函数。

回顾一下我们的任务目标：我们定义了逻辑回归公式$\hat{y}=\sigma (w^{T}x+b)$，我们希望$\hat{y}$尽可能和$y$相近。这里的“相近”，就是我们的优化目标。损失函数，可以看成是$y,\hat{y}$间的“距离”。

逻辑回归中，定义了每个输出和真值的误差函数（Loss Function），这个误差函数叫交叉熵
$$L(\hat{y},y)=-(ylog\hat{y}+(1-y)log(1-\hat{y}))$$

不使用另一种常见的误差函数均方误差的原因是，交叉熵较均方误差梯度更加平滑，更容易在之后的优化中找到全局最优解。

误差函数是定义在每个样本上的，而损失函数是定义在整个样本上的，表示所有样本误差的“总和”。这个“总和”其实就是平均值，即损失函数$J(w,b)$为:
$$J(w,b)=\frac{1}{m}{\Sigma }_{i=1}^m-(y^{(i)}log{\hat{y}}^{(i)}+(1-y^{(i)})log(1-{\hat{y}}^{(i)}))$$

优化算法——梯度下降

有了优化目标，接下来的问题就是如何用优化算法求出最优值。这里使用的是梯度下降（Gradient Descent） 法。梯度下降的思想很符合直觉：如果要让函数值更小，就应该让函数的输入沿着函数值下降最快的方向（梯度的方向）移动。

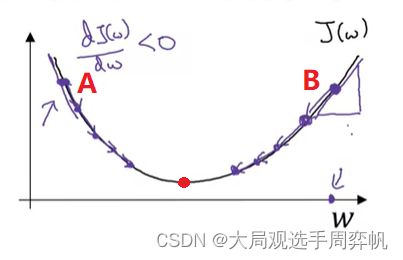
以课件中的一元函数为例：

一元函数的梯度值就是导数值，方向只有正和负两个方向。我们要根据每个点的导数，让每个点向左或向右“运动”，以使函数值更小。

从图像里可以看出，如果是参数最开始在A点，则往右走函数值才会变少；反之，对于B点，则应该往左移动。

每个点都应该向最小值“一小步一小步”地移动，直至抵达最低点。为什么要“一小步”移动呢？可以想象，如果一次移动的“步伐”过大，改变参数不仅不会让优化函数变小，甚至会让待优化函数变大。比如从A点开始，同样是往右移动，如果“步伐”过大，A点就会迈过最低点的红点，甚至跑到B点的上面。那么这样下去，待优化函数会越来越大，优化就失败了。

为了让优化能顺利进行，梯度下降法使用学习率（Learning Rate) 来控制参数优化的“步伐”，即用如下方法更新损失函数$J(w)$的参数：

$$\begin{gathered} Repeat: \\ w\leftarrow w-\alpha \frac{dJ}{dw} \end{gathered}$$

这里的 $\alpha$ 就是学习率，它控制了每次梯度更新的幅度。

其实这里还有两个问题：参数$w$该如何初始化；该执行梯度下降多少次。在这个问题中初始化对结果影响不大，可以简单地令$w=0$。而优化的次数没有硬性的需求，先执行若干次，根据误差是否收敛再决定是否继续优化即可。

前置知识补充

到这里，逻辑回归的知识已经讲完了。让我们梳理一下：

在逻辑回归问题中，我们有输入样本集$X$和其对应的期望输出$Y$，我们希望找到拟合函数$\hat{Y}=w^{T}X+b$，使得$\hat{Y}$和$Y$尽可能接近，即让损失函数$J(w,b)=mean(-(Ylog\hat{Y}+(1-Y)log(1-\hat{Y})))$尽可能小。

这里的$X,Y,\hat{Y}$表示的是全体样本。稍后我们会讨论如何用公式表示全体样本的计算。

我们可以用$0$来初始化所有待优化参数$w,b$，并执行梯度下降

$$\begin{array}{rl}w& \leftarrow w-\alpha \frac{dJ}{dw}\\ b& \leftarrow b-\alpha \frac{dJ}{db}\end{array}$$

若干次后得到一个较优的拟合函数。

为了让大家成功用代码实现逻辑回归，这门课贴心地给大家补充了数学知识和编程知识。

在我的笔记中，补充编程知识的记录会潦草一些。

求导

这部分对中国学生来说十分简单，因为求导公式是高中教材的内容。

导数即函数每时每刻的变化率，比如位移对时间的导数就是速度。以常见函数为例，对于直线$y=kx$，函数的变化率时时刻刻都是$k$；对于二次函数$y=x^2$，$x$处的导数是$2x$。

计算图

其实，所有复杂的数学运算都可以拆成计算图表示法。

计算图中的"图"其实是一个计算机概念，表示由节点和边组成的集合。不熟悉的话，当成日常用语里的图来理解也无妨。

比如上图中，哪怕是简单的运算$2a+b$，也可以拆成两步：先算$2\times a$，再算$(2a)+b$。

这里的“步”指原子运算，即最简单的运算。原子运算可以是加减乘除，也可以是求指数、求对数。复杂的运算，只是对简单运算的组合、嵌套。

明明简简单单可以用一行公式表示的事，要费很大的功夫画一张计算图呢？这是因为，对函数求导满足“链式法则”，借助计算图，可以更方便地用链式法则算出所有参数的导数。比如在上图中要求$f$对$a$的导数，使用链式法则的话，可以通过先求$f$对$c$的导数，再求$c$对$a$的导数得到。

利用计算图对逻辑回归求导

逻辑回归有计算图：

现在利用链式法则从右向左求导：

$$\begin{array}{rl}z& =w_1{x}_1+w_2{x}_2+b\\ a& =\frac{1}{1+e^{-z}}\\ L& =-(yloga+(1-y)log(1-a))\\ & \\ \frac{dL}{da}& =-(\frac{y}{a}-\frac{1-y}{1-a})\\ \frac{da}{dz}& =\frac{e^{-z}}{(1+e^{-z}{)}^2}=a(1-a)\\ \frac{dL}{dz}& =\frac{dL}{da}\frac{da}{dz}\\ & =-(\frac{y}{a}-\frac{1-y}{1-a})\times a(1-a)\\ & =-(y(1-a)-(1-y)a)\\ & =-(y-ya-a+ya)\\ & =a-y\\ \frac{dL}{d{w}_i}& =\frac{dL}{dz}\frac{dz}{d{w}_i}=(a-y)x_i\\ \frac{dL}{db}& =\frac{dL}{dz}\frac{dz}{db}=(a-y)\end{array}$$

这些运算里最难“注意到”的是$\frac{e^{-z}}{(1+e^{-z}{)}^2}=a(1-a)$。

在学计算机科学的知识时，可以适当忽略一些数学证明，把算好的公式直接拿来用，比如这里的$\frac{dL}{dz}=a-y$。

$\frac{dL}{d{w}_i},\frac{dL}{db}$就是我们要的梯度了，用它们去更新原来的参数即可。值得一提的是，这里的梯度是对一个样本而言。对于全部$m$个样本来说，本轮的梯度应该是所有样本的梯度的平均值。后面我们会学习如何对所有样本求导。

Python 向量化计算

在刚刚的一轮迭代中，我们要用到两次循环：

1. 对$m$个样本循环处理
2. 对$n_x$个权重$w_i$与对应的$x_i$相乘

直接拿 Python 写这些 for 循环，程序会跑得很慢的，这里最好使用向量化计算。在这一节里我们补充一下 Python 基础知识，下一节介绍怎么用它们实现逻辑回归的向量化实现。

课程中提到向量化的好处是可以用SIMD（单指令多数据流）优化，这个概念可以理解成计算机会同时对16个或32个数做计算。如果输入的数据是向量的话，相比一个一个做for循环，一次算16,32个数的计算速度会更快。

但实际上，除了无法使用SIMD以外，Python的低效也是拖慢速度的原因之一。哪怕是不用SIMD，单纯地用C++的for循环实现向量化计算，都能比用Python的循环快上很多。

Python 的 numpy 库提供了向量化计算的接口。比如以下是向量化的例子：

import numpy as np
a = np.zeros((10)) # 新建长度为10的向量，值为0
b = np.ones((10)) # 新建长度为10的向量，值为1
a = a + b # 10个数同时做加法
a = np.exp(a) # 对10个数都做指数运算

numpy 允许一种叫做“广播”的操作，这种操作能够完成不同形状数据间的运算。

a = np.ones(10) # a的形状:[10]
k = np.array([3]) # 用列表[3]新建张量，k的形状:[1]
a = k * a # 广播

这里k的shape为[1]，a的shape为[10]。用k乘a，实际上就是令a[i] = k[0] * a[i]。也就是说，k[0]“广播”到了a的每一个元素上。

有一种快速理解广播的方法：可以认为k的形状从[1]变成了[10]，再让k和a逐个元素做乘法。

同理，如果用一个a[x, y]的矩阵加一个b[x, 1]的矩阵，实际上是做了下面的运算：

for i in range(x):
  for j in range(y):
    a[i, j] = a[i, j] + b[i, 0] 

用刚刚介绍的方法来理解，可以认为b从[x, 1]扩充成了[x, y]，再和a做逐个元素的加法运算。

向量化计算前向和反向传播

现在，有了求导的基础知识和向量化计算的基础知识，让我们来写一下如何用矩阵表示逻辑回归中的运算，并用Python代码描述这些计算过程。

单样本的正向传播：

$$\hat{y}=a=\sigma (w^{T}x+b)$$

推广到多样本：

$$\hat{Y}=A=\sigma (w^{T}X+b)$$

这里的$X,A,\hat{Y}$是把原来单样本的列向量$x_i,{\hat{y}}_i$横向堆叠起来形成的矩阵，即:

$$[\widehat{y_1},...,\widehat{y_m}]=\sigma ([w^T{x}_1+b,...,w^T{x}_m+b])$$

单样本反向传播：
$$\begin{array}{rl}dz& =a-y\\ d{w}_i& =dz\cdot x_i\\ dw& =\left[\begin{array}{c}d{w}_1\\ ...\\ d{w}_{n_x}\end{array}\right]=\left[\begin{array}{c}dz\cdot x_1\\ ...\\ dz\cdot x_{n_x}\end{array}\right]=dz\ast x\\ db& =dz\end{array}$$

$dz$ 是 $\frac{dJ}{dz}$的简写，其他变量同理。编程时也按同样的方式命名。

所有的$\ast$都表示逐元素乘法。比如$[1,2,3]\ast [1,2,3]=[1,4,9]$。$\ast$满足前面提到的广播，比如$[2]\ast [1,2,3]=[2,4,6]$。

多样本反向传播：

$$\begin{array}{rl}dZ& =A-Y\\ d{w}_i& =X_{i}d{Z}^T=d{z}^{(1)}{x}_i^{(1)}+...+d{z}^{(m)}{x}_i^{(m)}\\ dw& =\frac{1}{m}\left[\begin{array}{c}d{w}_1\\ ...\\ d{w}_{n_x}\end{array}\right]=\frac{1}{m}\left[\begin{array}{ccc}d{z}^{(1)}{x}_1^{(1)}+& ...& +d{z}^{(m)}{x}_1^{(m)}\\ ...& ...& ...\\ d{z}^{(1)}{x}_{n_x}^{(1)}+& ...& +d{z}^{(m)}{x}_{n_x}^{(m)}\end{array}\right]\\ & =\frac{1}{m}Xd{Z}^T\\ db& =\frac{1}{m}{\Sigma }_{i=1}^{m}d{Z}^{(i)}\end{array}$$

用代码描述多样本前向传播和反向传播就是：

Z = np.dot(w.T, x)+b
A = sigmoid(Z)
dZ = A-Y
dw = np.dot(X, dZ.T) / m
db = np.mean(dZ)
# db=np.sum(dZ) / m

np.dot实现了求向量内积或矩阵乘法，np.sum实现了求和，np.mean实现了求均值。

总结

这堂课的主要知识点有：

• 什么是二分类问题。
• 如何对建立逻辑回归模型。
  • Sigmoid 函数 $\sigma (z)=\frac{1}{1+e^{-z}}$
• 误差函数与损失函数
  • 逻辑回归的误差函数：$L(\hat{y},y)=-(ylog\hat{y}+(1-y)log(1-\hat{y}))$
• 用梯度下降算法优化损失函数
• 计算图的概念及如何利用计算图算梯度

学完这堂课后，应该掌握的编程技能有：

• 了解numpy基本知识
  • resize
  • .T
  • exp
  • dot
  • mean, sum
• 用numpy做向量化计算
• 实现逻辑回归
  • 对输入数据做reshape的预处理
  • 用向量化计算算$\hat{y}$及参数的梯度
  • 迭代优化损失函数

代码实战

这节课有两个编程作业:第一个作业要求使用numpy实现对张量的一些操作，第二个作业要求用逻辑回归实现一个分类器。这些编程作业是在python的notebook上编写的。每道题给出了代码框架，只要写关键的几行代码就行。对我来说，编程体验极差。作为编程最强王者，怎能受此“嗟来之码”的屈辱？我决定从零开始，自己收集数据，并用numpy实现逻辑回归。

其实我不分享作业代码的真正原因是：Coursera不允许公开展示作业代码。在之后的笔记中，我也会分享如何用自己的代码实现每堂课的编程目标。

这篇笔记用到的代码已在GitHub上开源：https://github.com/SingleZombie/DL-Demos/tree/master/dldemos/LogisticRegression 。下文展示的代码和原本的代码有略微的出入，建议大家对着源代码阅读后文。

程序设计

不管写什么程序，都要先想好整体的架构，再开始动手写代码。

深度学习项目的架构比较固定。一般一个深度学习项目由以下几部分组成：

• 数据预处理
• 定义网络结构
• 定义损失函数
• 定义优化策略
• 用训练pipeline串联起网络、损失函数、优化策略
• 测试模型精度

当然，实现深度学习项目比一般的编程项目多一个步骤：除了写代码外，完成深度学习项目还需要收集数据。

接下来，我将按照数据收集、数据处理、网络结构、损失函数、训练、测试这几部分介绍这个项目。之后的笔记也会以这个形式介绍编程项目。

数据收集

说起最经典的二分类任务，大家都会想起小猫分类（或许跟吴恩达老师的课比较流行有关）。在这个项目中，我也顺应潮流，选择了一个猫狗数据集（https://www.kaggle.com/datasets/fusicfenta/cat-and-dog?resource=download）。

在此数据集中，数据是按以下结构存储的：

在二分类任务中，数据的标签为0或1（表示是否是小猫）。而此数据集只是把猫、狗的图片分别放到了不同的文件夹里，这意味着我们待会儿要手动给这些数据打上0或1的标签。

数据预处理

由于训练集和测试集的目录结构相同，我们先写一个读数据集的函数：

input_shape=(224, 224)
def load_dataset(dir, data_num):
    cat_images = glob(osp.join(dir, 'cats', '*.jpg'))
    dog_images = glob(osp.join(dir, 'dogs', '*.jpg'))
    cat_tensor = []
    dog_tensor = []

    for idx, image in enumerate(cat_images):
        if idx >= data_num:
            break
        i = cv2.imread(image) / 255
        i = cv2.resize(i, input_shape)
        cat_tensor.append(i)

    for idx, image in enumerate(dog_images):
        if idx >= data_num:
            break
        i = cv2.imread(image) / 255
        i = cv2.resize(i, input_shape)
        dog_tensor.append(i)

    X = cat_tensor + dog_tensor
    Y = [1] * len(cat_tensor) + [0] * len(dog_tensor)
    X_Y = list(zip(X, Y))
    shuffle(X_Y)
    X, Y = zip(*X_Y)
    return X, Y

函数先是用glob读出文件夹下所有猫狗的图片路径，再按文件路径依次把文件读入。接着，函数为数据生成了0或1的标签。最后，函数把数据打乱，并返回数据。让我们来看看这段代码里有哪些要注意的地方。

在具体介绍代码之前，要说明一下我在这个数据集上做的两个特殊处理：

1. 这个函数有一个参数data_num，表示我们要读取data_num张猫+data_num张狗的数据。原数据集有上千张图片，直接读进内存肯定会把内存塞爆。为了实现上的方便，我加了一个控制数据数量的参数。在这个项目中，我只用了800张图片做训练集。
2. 原图片是很大的，为了节约内存，我把所有图片都变成了input_shape=(224, 224)的大小。

接下来，我们再了解一下数据处理中的一些知识。在读数据的时候，把数据归一化（令数据分布在(-1, 1)这个区间内）十分关键。如果不这样做的话，loss里的$log{e}^z$会趋近$log0$，梯度的收敛速度会极慢，训练会难以进行。这是这节课上没有讲的内容，但是它在实战中非常关键。

这个时候输出loss的话，会得到一个Python无法表示的数字：nan。在训练中如果看到loss是nan，多半就是数据没有归一化的原因。这个是一个非常常见的bug，一定要记得做数据归一化！

第三节课里讲了激活函数的收敛速度问题。

现在来详细看代码。

下面的代码用于从文件系统中读取所有图片文件，并把文件的绝对路径保存进一个list。如果大家有疑问，可以自行搜索glob函数的用法。

cat_images = glob(osp.join(dir, 'cats', '*.jpg'))
dog_images = glob(osp.join(dir, 'dogs', '*.jpg'))

在之后的两段for循环中，我们通过设定循环次数来控制读取的图片数。在循环里，我们先读入文件，再归一化文件，最后把图片resize到(224, 224)。

for idx, image in enumerate(cat_images):
    if idx >= data_num:
        break
    i = cv2.imread(image) / 255
    i = cv2.resize(i, input_shape)
    cat_tensor.append(i)

在这段代码里，归一化是靠

i = cv2.imread(image) / 255

实现的。

这里我们知道输入是图像，颜色通道最大值是255，所以才这样归一化。在很多问题中，我们并不知道数据的边界是多少，这个时候只能用普通的归一化方法了。一种简单的归一化方法是把每个输入向量的模设为1。后面的课程里会详细介绍归一化方法。

读完数据后，我们用以下代码生成了训练输入和对应的标签：

X = cat_tensor + dog_tensor
Y = [1] * len(cat_tensor) + [0] * len(dog_tensor)

Python里，[1] * 10可以把列表[1]复制10次。

现在，我们的数据是“[猫，猫，猫……狗，狗，狗]”这样整整齐齐地排列着，没有打乱。由于我们是一次性拿整个训练集去训练，训练数据不打乱倒也没事。但为了兼容之后其他训练策略，这里我还是习惯性地把数据打乱了：

X_Y = list(zip(X, Y))
shuffle(X_Y)
X, Y = zip(*X_Y)

使用这三行“魔法Python”可以打乱list对中的数据。

有了读一个文件夹的函数load_dataset，用下面的代码就可以读训练集和测试集：

def generate_data(dir='data/archive/dataset', input_shape=(224, 224)):
    train_X, train_Y = load_dataset(osp.join(dir, 'training_set'), 400)
    test_X, test_Y = load_dataset(osp.join(dir, 'test_set'), 100)
    return train_X, train_Y, test_X, test_Y

这里训练集有400+400=800张图片，测试集有100+100=200张图片。如果大家发现内存还是占用太多的话，可以改小这两个数字。

网络结构

在这个项目中，我们使用的是逻辑回归算法。它可以看成是只有一个神经元的神经网络。如之前的课堂笔记所述，我们网络的公式是：

$$\hat{y}=\sigma (w^{T}x+b)$$

这里我们要实现两个函数：

1. resize_input：由于图片张量的形状是[h, w, c]（高、宽、颜色通道），而网络的输入是一个列向量，我们要把图片张量resize一下。
2. sigmoid: 我们要用numpy函数组合出一个sigmoid函数。

熟悉了numpy的API后，实现这两个函数还是很容易的：

def resize_input(a: np.ndarray):
    h, w, c = a.shape
    a.resize((h * w * c))
    return a

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

这里我代码实现上写得有点“脏”，调用resize_input做数据预处理是放在main函数里的：

train_X, train_Y, test_X, test_Y = generate_data()

train_X = [resize_input(x) for x in train_X]
test_X = [resize_input(x) for x in test_X]
train_X = np.array(train_X).T
train_Y = np.array(train_Y)
train_Y = train_Y.reshape((1, -1))
test_X = np.array(test_X).T
test_Y = np.array(test_Y)
test_Y = test_Y.reshape((1, -1))

array = array.reshape(a, b) 等价于 array.resize(a, b)。但是，reshape的某一维可以写成-1，表示这一维的大小让程序自己用除法算出来。比如总共有a * b个元素，调用reshape(-1, a)，-1的那一维会变成b。

经过这些预处理代码，X的shape会变成[$n_x$, $m$]，Y的shape会变成[$1$, $m$]，和课堂里讲的内容一致。

有了sigmoid函数和正确shape的输入，我们可以写出网络的推理函数：

def predict(w, b, X):
    return sigmoid(np.dot(w.T, X) + b)

损失函数与梯度下降

如前面的笔记所述，损失函数可以用下面的方法计算：

def loss(y_hat, y):
    return np.mean(-(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)))

我们定义损失函数，实际上为了求得每个参数的梯度。在求梯度时，其实用不到损失函数本身，只需要知道每个参数对于损失函数的导数。在这个项目中，损失函数只用于输出，以监控当前的训练进度。

而在梯度下降中，我们不需要用到损失函数，只需要算出每个参数的梯度并执行梯度下降：

def train_step(w, b, X, Y, lr):
    m = X.shape[1]
    Z = np.dot(w.T, X) + b
    A = sigmoid(Z)
    d_Z = A - Y
    d_w = np.dot(X, d_Z.T) / m
    d_b = np.mean(d_Z)
    return w - lr * d_w, b - lr * d_b

在这段代码中，我们根据前面算好的公式，算出了w, b的梯度并对w, b进行更新。

训练

def init_weights(n_x=224 * 224 * 3):
    w = np.zeros((n_x, 1))
    b = 0.0
    return w, b

def train(train_X, train_Y, step=1000, learning_rate=0.00001):
    w, b = init_weights()
    print(f'learning rate: {learning_rate}')
    for i in range(step):
        w, b = train_step(w, b, train_X, train_Y, learning_rate)

        # 输出当前训练进度
        if i % 10 == 0:
            y_hat = predict(w, b, train_X)
            ls = loss(y_hat, train_Y)
            print(f'step {i} loss: {ls}')
    return w, b

有了刚刚的梯度下降函数train_step，训练实现起来就很方便了。我们只需要设置一个训练总次数step，再调用train_step更新参数即可。

测试

在深度学习中，我们要用一个网络从来没有见过的数据集做测试，以验证网络能否泛化到一般的数据上。这里我们直接使用数据集中的test_set，用下面的代码计算分类任务的准确率：

def test(w, b, test_X, test_Y):
    y_hat = predict(w, b, test_X)
    predicts = np.where(y_hat > 0.5, 1, 0)
    score = np.mean(np.where(predicts == test_Y, 1, 0))
    print(f'Accuracy: {score}')

这里的np.where没有在课堂里讲过，这里补充介绍一下。predicts=np.where(y_hat > 0.5, 1, 0)这一行，等价于下面的循环：

# 新建一个和y_hat一样形状的ndarray
predicts = np.zeros(y_hat.shape)
for i, v in enumerate(y_hat):
  if v > 0.5:
    predicts[i] = 1
  else:
    predicts[i] = 0

也就是说，我们对y_hat做了逐元素的判断v > 0.5?，如果判断成立，则赋值1，否则赋值0。这就好像是一个老师在批改学生的作业，如果对了，就给1分，否则给0分。

y_hat > 0.5是有实际意义的：在二分类问题中，如果网络输出图片是小猫的概率大于0.5，我们就认为图片就是小猫的图片；否则，我们认为不是。

之后，我们用另一个(np.where(predicts == test_Y, 1, 0)来“批改作业”：如果预测值和真值一样，则打1分，否则打0分。

最后，我们用score = np.mean(...)算出每道题分数的平均值，来给整个网络的表现打一个总分。

这里要注意一下，整个项目中我们用了两个方式来评价网络：我们监控了loss,因为loss反映了网络在训练集上的表现；我们计算了网络在测试集上的准确度，因为准确度反映了网络在一般数据上的表现。之后的课堂里应该也会讲到如何使用这些指标来进一步优化网络，这里会算它们就行了。

调参

嘿嘿，想不到吧，除了之前计划的章节外，这里还多了一个趣味性比较强的调参章节。

搞深度学习，最好玩的地方就是调参数了。通过优化网络的超参数，我们能看到网络的性能在不断变好，准确率在不断变高。这个感觉就和考试分数越来越高，玩游戏刷的伤害越来越高给人带来的成就感一样。

在这个网络中，可以调的参数只有一个学习率。通过玩这个参数，我们能够更直观地认识学习率对梯度下降的影响。

这里我分享一下我的调参结果：

如果学习率>=0.0003，网络更新的步伐过大，从而导致梯度不收敛，训练失败。

learning rate: 0.0003
step 0 loss: 0.6918513655136874
step 10 loss: 0.9047000002073068
step 20 loss: 0.9751763789675365

学习率==0.0002的话，网络差不多能以最快的速度收敛。

learning rate: 0.0002
step 0 loss: 0.692168431534233
step 10 loss: 0.684254876013497
step 20 loss: 0.6780829877162996

学习率0.0001,甚至0.00003也能训练，但是训练速度会变慢。

learning rate: 0.0001
step 0 loss: 0.6926003513589579
step 10 loss: 0.6883167092427446
step 20 loss: 0.684621635180076

这里判断网络的收敛速度时，要用到的指标是损失函数。我的代码里默认每10次训练输出一次损失函数的值。

一般大家不会区别误差和损失函数，会把损失函数叫成 loss。

为了节约时间，一开始我只训练了1000步，最后准确率只有0.57左右。哪怕我令输出全部为1，从期望上都能得到0.5的准确率。这个结果确实不尽如人意。

我自己亲手设计的模型，结果怎么能这么差呢？肯定是训练得不够。我一怒之下，加了个零，让程序跑10000步训练。看着loss不断降低，从0.69，到0.4，再到0.3，最后在0.24的小数点第3位之后变动，我的心情也越来越激动：能不能再低点，能不能再创新低？那感觉就像股市开盘看到自己买的股票高开，不断祈祷庄家快点买入一样。

在电脑前，盯着不断更新的控制台快一小时后，loss定格在了0.2385，我总算等到了10000步训练结束的那一刻。模型即将完成测试，准确率即将揭晓。
我定睛一看——准确率居然还只有0.575!

这肯定不是我代码的问题，一定是逻辑回归这个模型太烂了！希望在之后的课程中，我们能够用更复杂的模型跑出更好的结果。

欢迎大家也去下载这个demo，一起调一调参数~