链表题目:K 个一组反转链表
文章目录
- 题目
-
- 标题和出处
- 难度
- 题目描述
-
- 要求
- 示例
- 数据范围
- 进阶
- 解法一
-
- 思路和算法
- 代码
- 复杂度分析
- 解法二
-
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:K 个一组反转链表
出处:25. K 个一组反转链表
难度
4 级
题目描述
要求
给你一个链表,每 k \texttt{k} k 个结点一组进行反转,并返回反转后的链表。
k \texttt{k} k 是一个正整数,它的值小于或等于链表的长度。如果结点总数不是 k \texttt{k} k 的倍数,那么请将最后剩余的结点保持原有顺序。
不能修改结点的值,只能修改结点本身。
示例
示例 1:
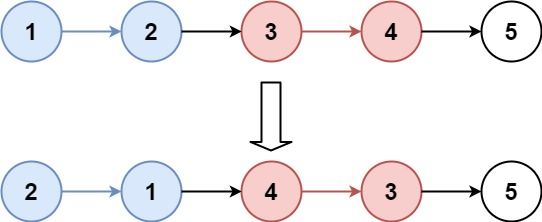
输入: head = [1,2,3,4,5], k = 2 \texttt{head = [1,2,3,4,5], k = 2} head = [1,2,3,4,5], k = 2
输出: [2,1,4,3,5] \texttt{[2,1,4,3,5]} [2,1,4,3,5]
示例 2:
输入: head = [1,2,3,4,5], k = 3 \texttt{head = [1,2,3,4,5], k = 3} head = [1,2,3,4,5], k = 3
输出: [3,2,1,4,5] \texttt{[3,2,1,4,5]} [3,2,1,4,5]
示例 3:
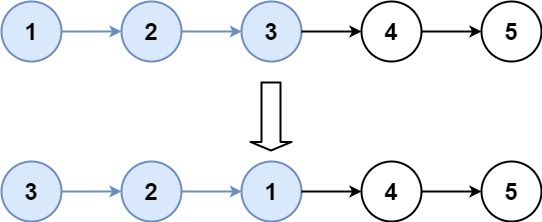
输入: head = [1,2,3,4,5], k = 1 \texttt{head = [1,2,3,4,5], k = 1} head = [1,2,3,4,5], k = 1
输出: [1,2,3,4,5] \texttt{[1,2,3,4,5]} [1,2,3,4,5]
示例 4:
输入: head = [1], k = 1 \texttt{head = [1], k = 1} head = [1], k = 1
输出: [1] \texttt{[1]} [1]
数据范围
- 链表中结点的数目是 sz \texttt{sz} sz
- 1 ≤ sz ≤ 5000 \texttt{1} \le \texttt{sz} \le \texttt{5000} 1≤sz≤5000
- 0 ≤ Node.val ≤ 1000 \texttt{0} \le \texttt{Node.val} \le \texttt{1000} 0≤Node.val≤1000
- 1 ≤ k ≤ sz \texttt{1} \le \texttt{k} \le \texttt{sz} 1≤k≤sz
进阶
你能使用 O(1) \texttt{O(1)} O(1) 额外空间实现吗?
解法一
思路和算法
不考虑空间复杂度的要求,可以使用数组存储链表的结点,然后在数组中完成链表的反转。
从链表的头结点开始遍历链表,依次将每个结点添加到数组中,遍历结束之后,数组中有 sz \textit{sz} sz 个结点,其中 sz \textit{sz} sz 是链表的长度,且数组中的结点顺序和链表中的结点顺序相同。
然后对数组中的每组 k k k 个元素进行反转。用 index \textit{index} index 表示当前组的结束下标,初始时 index = k − 1 \textit{index} = k - 1 index=k−1,则当前组的开始下标是 index − k + 1 \textit{index} - k + 1 index−k+1。对当前组进行反转的操作如下:
-
将 left \textit{left} left 和 right \textit{right} right 分别初始化为当前组的开始下标和结束下标;
-
交换 left \textit{left} left 和 right \textit{right} right 处的结点;
-
将 left \textit{left} left 加 1 1 1, right \textit{right} right 减 1 1 1,重复上述两步操作,直到 left ≥ right \textit{left} \ge \textit{right} left≥right 为止。
当前组完成反转之后,将 index \textit{index} index 的值加 k k k,即进入下一组,对下一组继续进行反转操作。由于只会对 k k k 个结点的组进行反转操作,因此反转操作可以继续的条件是 index < sz \textit{index} < \textit{sz} index<sz,当 index ≥ sz \textit{index} \ge \textit{sz} index≥sz 时反转结束。
反转结束后,只是数组中的结点顺序为反转之后的顺序,结点之间的指针关系尚未更新。为了完成反转操作,需要更新结点之间的指针关系,因此遍历数组,对于任意两个相邻的结点,前一个结点的 next \textit{next} next 指针应指向后一个结点,最后一个结点的 next \textit{next} next 指针应指向 null \text{null} null,否则会导致链表中出现环。
更新结点之间的指针关系之后,整个链表的反转完成,返回数组中的首个元素(即下标 0 0 0 处的元素)。
代码
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
List<ListNode> nodes = new ArrayList<ListNode>();
ListNode temp = head;
while (temp != null) {
nodes.add(temp);
temp = temp.next;
}
int sz = nodes.size();
int index = k - 1;
while (index < sz) {
int left = index - k + 1, right = index;
while (left < right) {
ListNode node = nodes.get(left);
nodes.set(left, nodes.get(right));
nodes.set(right, node);
left++;
right--;
}
index += k;
}
for (int i = 0; i < sz - 1; i++) {
nodes.get(i).next = nodes.get(i + 1);
}
nodes.get(sz - 1).next = null;
return nodes.get(0);
}
}
复杂度分析
-
时间复杂度: O ( sz ) O(\textit{sz}) O(sz),其中 sz \textit{sz} sz 是链表的长度。一共需要遍历链表三次。
-
空间复杂度: O ( sz ) O(\textit{sz}) O(sz),其中 sz \textit{sz} sz 是链表的长度。需要使用数组存储链表的每个结点。
解法二
思路和算法
如果要将空间复杂度降到 O ( 1 ) O(1) O(1),就不能用数组或者其他数据结构存储结点,而是在遍历的过程中完成反转。
由于新链表的头结点和原始链表的头结点不同,因此需要创建哑结点 dummyHead \textit{dummyHead} dummyHead,使得 dummyHead . next = head \textit{dummyHead}.\textit{next} = \textit{head} dummyHead.next=head。从 dummyHead \textit{dummyHead} dummyHead 开始,如果后面有至少 k k k 个结点,则将后面的 k k k 个结点反转,然后定位到反转后的这 k k k 个结点的尾结点,继续对后面的结点按照 k k k 个一组反转,直到剩余的结点少于 k k k 个。
将 prev \textit{prev} prev 初始化为 dummyHead \textit{dummyHead} dummyHead,根据 prev \textit{prev} prev 定位到下一组 k k k 个结点的开始结点和结束结点: start \textit{start} start 为 prev \textit{prev} prev 的后面第 1 1 1 个结点, end \textit{end} end 为 prev \textit{prev} prev 的后面第 k k k 个结点,当 prev \textit{prev} prev 的后面不足 k k k 个结点时 end = null \textit{end} = \text{null} end=null。
如果 end = null \textit{end} = \text{null} end=null,则说明剩余的结点少于 k k k 个,反转结束。如果 end ≠ null \textit{end} \ne \text{null} end=null,则从 start \textit{start} start 到 end \textit{end} end 有 k k k 个结点,需要对这 k k k 个结点进行反转操作。反转 k k k 个结点之后,需要更新这 k k k 个结点的首尾结点和前后相邻结点的连接关系,因此需要知道上一组的最后一个结点和下一组的第一个结点。上一组的最后一个结点为 prev \textit{prev} prev。为了得到下一组的第一个结点,令 next = end . next \textit{next} = \textit{end}.\textit{next} next=end.next,则 next \textit{next} next 为下一组的第一个结点。
反转从 start \textit{start} start 到 end \textit{end} end 的 k k k 个结点,可以参考「反转链表」的做法,区别在于这里只对 k k k 个结点进行反转。
完成 k k k 个结点的反转之后,这 k k k 个结点的开始结点和结束结点分别变成 end \textit{end} end 和 start \textit{start} start,因此令 prev . next \textit{prev}.\textit{next} prev.next 指向 end \textit{end} end, start . next \textit{start}.\textit{next} start.next 指向 next \textit{next} next,即完成这 k k k 个结点的首尾结点和前后相邻结点的连接关系的更新。
将 prev \textit{prev} prev 指向 start \textit{start} start,则 prev \textit{prev} prev 位于当前反转后的 k k k 个结点的最后一个结点, prev . next \textit{prev}.\textit{next} prev.next 即为下一组的第一个结点。继续对剩下的结点进行反转,直到整个链表反转完毕。
整个链表反转完毕之后,返回 dummyHead . next \textit{dummyHead}.\textit{next} dummyHead.next。
代码
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode dummyHead = new ListNode(0, head);
ListNode prev = dummyHead;
ListNode end = dummyHead;
while (end.next != null) {
for (int i = 0; i < k && end != null; i++) {
end = end.next;
}
if (end == null) {
break;
}
ListNode start = prev.next;
ListNode next = end.next;
reverseGroup(start, k);
prev.next = end;
start.next = next;
prev = start;
end = start;
}
return dummyHead.next;
}
public ListNode reverseGroup(ListNode head, int k) {
ListNode prev = null, curr = head;
for (int i = 0; i < k; i++) {
ListNode next = curr.next;
curr.next = prev;
prev = curr;
curr = next;
}
return prev;
}
}
复杂度分析
-
时间复杂度: O ( sz ) O(\textit{sz}) O(sz),其中 sz \textit{sz} sz 是链表的长度。遍历每组 k k k 个结点的开始结点和结束结点需要遍历链表中的每个结点一次,反转每组 k k k 个结点也需要遍历链表中的每个结点一次。
-
空间复杂度: O ( 1 ) O(1) O(1)。