数位Dp模型与题目详解acm

---

#写在前面

树的形式是一种分类讨论的思想

##度的数量

https://www.acwing.com/problem/content/1083/

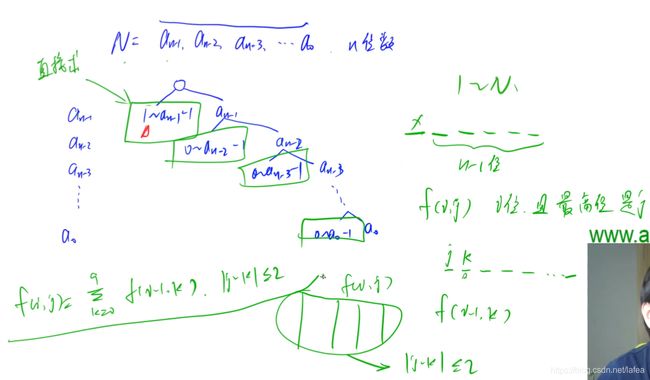
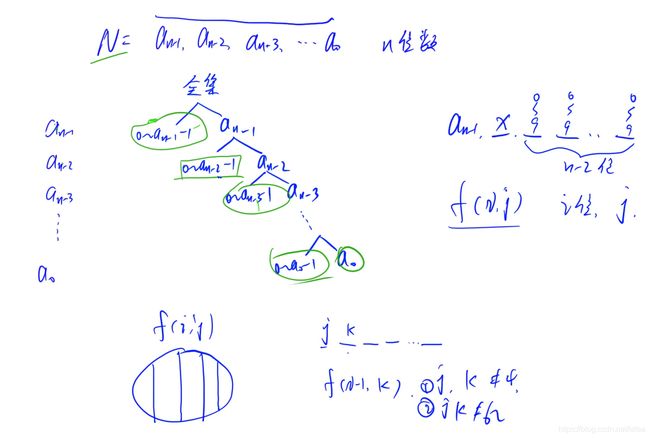
可以看到我们用了类似一棵树的形式讨论问题
这里注意，当B进制下n的某一位上已经是1的时候，我们是直接轮到下一位上进行讨论的，所以当最末尾一位是1且刚好满足有K个的时候（即为last==K）的时候，我们要手动给res+1

----c++版

#include
#include
using namespace std;
#include
const int N=35;
int f[N][N];
int K,B;

void init(){//通过公式推出组合数Cij
    for(int i=0; i<N; i++)
        for(int j=0; j<=i; j++)
            if(!i)f[i][j]=1;
            else f[i][j] = f[i-1][j]+f[i-1][j-1];
}

int dp(int n){
    if(!n) return 0;
    
    vector<int> nums;
    while(n) nums.push_back(n%B), n/=B;//搞出B进制下的n
    
    int res=0;//答案
    int last=0;//右边分支往下走的前缀的一些信息，存已经有了几个1
    
    for(int i=nums.size()-1; i>=0; i--){
        int x=nums[i];
        if(x){//求左边分支中数的个数
            res+=f[i][K-last];//无论第i位是否是1，这一位都可以有
            //代码这里写得可能有点绕，但是当x=1的时候我们确实在这里算了，
            //必须在这里算了，因为之后我们是对last做处理而不是对res
            if(x>1){
                if(K-last-1>=0)res+=f[i][K-last-1];
                break;
            }else{
                last++;
                if(last>K)break;
            }
        }
    if(!i&&last==K)res++;
    }
    return res;
}

int main(){
    init();
    int l,r;
    cin>>l>>r>>K>>B;
    
    cout<<dp(r)-dp(l-1)<<endl;
    
    return 0;
}

##数字游戏

https://www.acwing.com/problem/content/1084/

一般树的左边都可以通过dp预处理出来，右边就是n本身

----c++版

#include
#include
using namespace std;
#include
#include
const int N=15;
int f[N][N];

void init(){
    for(int i=0; i<=9; i++) f[1][i]=1;
    
    for(int i=2;  i<N; i++)
        for(int j=0; j<=9; j++)
            for(int k=j; k<=9; k++)
                f[i][j]+=f[i-1][k];
}

int dp(int n){
    if(!n) return 1;
    vector<int> nums;
    while(n)nums.push_back(n%10), n/=10;
    
    int res=0, last=0;
    for(int i=nums.size()-1; i>=0; i--){
        int x=nums[i];
    
        for(int j=last; j<x; j++)
            res+=f[i+1][j];
        if(x < last)break;
        last=x;
        if(!i)res++;
    }   
    return res;
}

int main(){
    init();
    int l,r;
    while(cin>>l>>r)cout<<dp(r)-dp(l-1)<<endl;
    
    return 0;
}

##windy数

https://www.acwing.com/problem/content/1085/

----c++版

#include
#include
#include
using namespace std;
#include
//这题比起上题，不能有前导零
const int N=11;
int f[N][10];

void init(){
    for(int i=0; i<=9; i++)f[1][i]=1;//0也算一种方案
    
    for(int i=2; i<N; i++)
        for(int j=0; j<=9; j++)
            for(int k=0; k<=9; k++)
                if(abs(j-k)>=2)
                    f[i][j]+=f[i-1][k];
}

int dp(int n){
    if(!n) return 0;
    vector<int> nums;
    while(n) nums.push_back(n%10), n/=10;
    
    int res=0;
    int last=-2;
    for(int i=nums.size()-1; i>=0; i--){
        int x=nums[i];
        for(int j= i==nums.size()-1 ; j<x; j++)
            if(abs(j-last)>=2)
                res+=f[i+1][j];
        
        if(abs(x-last)>=2)last=x;
        else break;
        
        if(!i)res++;
    }
    //特殊处理有前导零的数
    for(int i=1; i<nums.size(); i++)
        for(int j=1; j<=9; j++)
            res+=f[i][j];

    return res;
}

int main(){
    init();
    int l,r;
    cin>>l>>r;
    cout<<dp(r)-dp(l-1)<<endl;
    
    return 0;
}

## 数字游戏 II

https://www.acwing.com/problem/content/1086/

----c++版

#include
#include
#include
#include
using namespace std;
const int N=11, M=110;
int p;//取模数
int f[N][10][M];

int mod(int x, int y){//c++负数取模得到负的余数，为了得到正的余数，需要自己实现一个取模函数
    return (x%y+y)%y;
}

void init(){
    memset(f, 0, sizeof f);
    for(int i=0; i<=9; i++)f[1][i][i%p]++;
    
    for(int i=2; i<N; i++)
        for(int j=0; j<=9; j++)
            for(int k=0; k<p; k++)
                for(int x=0; x<=9; x++)
                    f[i][j][k] += f[i-1][x][mod(k-j, p)];
}

int dp(int n){
    if(!n) return 1;
    vector<int> nums;
    while(n) nums.push_back(n%10), n/=10;
    int res=0;
    int last=0;
    for(int i=nums.size()-1; i>=0; i--){
        int x=nums[i];
        for(int j=0; j<x; j++)
            res+=f[i+1][j][mod(-last, p)];
        
        last+=x;
        
        if(!i&&last%p==0)res++;
    }
    return res;
}

int main(){
    int l, r;
    while(cin>>l>>r>>p){
        init();
        cout<<dp(r)-dp(l-1)<<endl;
    }
    return 0;
    
    return 0;
}

##不要62

https://www.acwing.com/problem/content/1087/

数位DP+简单状态机

----c++版

#include
#include
#include
#include
using namespace std;
const int N=15; 
int f[N][10];

void init(){
    for(int i=0; i<=9; i++)
        if(i!=4)
            f[1][i]=1;
    
    for(int i=2; i<N; i++)
        for(int j=0; j<=9; j++){
            if(j==4)continue;
            for(int k=0; k<=9; k++){
                if(k==4||j==6&&k==2)continue;
                f[i][j]+=f[i-1][k];
            }
        }
}

int dp(int n){
    if(!n) return 1;
    vector<int> nums;
    while(n) nums.push_back(n%10), n/=10;
    
    int res=0;
    int last=0;
    for(int i=nums.size()-1; i>=0; i--){
        int x=nums[i];
        for(int j=0; j<x; j++){
            if(j==4||last==6&&j==2)continue;
            res+=f[i+1][j];
        }
        if(x==4||last==6&&x==2)break;//整个分支都是不必要的了
        last=x;
        if(!i)res++;
    }
    return res;
}

int main(){
    init();    
    int l,r;
    while(cin>>l>>r, l||r){
        cout<<dp(r)-dp(l-1)<<endl;
    }
    
    return 0;
}

##计数问题

https://www.acwing.com/problem/content/340/

----c++版

#include
#include
using namespace std;
//像小学数奥问题，分情况讨论
//[a,b], 0~9
//实现一个count(n, x)函数，统计1~n中x出现的次数
//于是问题可以转化为类似前缀和的区间操作
//count(b, x)-count(a-1, x);

//count的具体实现：
//先求某个数在每一位上出现的次数
//例子：求1在第四位上出现的次数，n是7位数
//1 <= xxx1yyy <=abcdefg
//一：xxx = 000~abc-1, yyy=000~999, 有abc*1000种
//二：当xxx=abc
//  二一：当d<1, abc1yyy>abc0efg, 0种
//  二二：当d=1, yyy=000~efg, efg+1种
//  二三：当d>1, yyy=000~999, 1000种

//关于边界问题：
//当求1在第一位出现的次数，第一大种情况不存在
//枚举数字0时候，要注意第一大类从001开始
#include

int get(vector<int>num, int l,int r){//第一大类前部分计数
    int res=0;
    for(int i=l;i>=r;i--) res=res*10+num[i];
    return res;
}

int power10(int x){
    int res=1;
    while(x--)res*=10;
    return res;
}

int count(int n,int x){
    if(!n)return 0;//蛋疼边界
    vector<int>num;//扣数字金典操作
    while(n){
        num.push_back(n%10);
        n/=10;
    }
    n=num.size();
    
    int res=0;
    for(int i=n-1-!x;i>=0;i--){
        if(i<n-1){//枚举最高位时不存在第一大类
            res+=get(num, n-1,i+1)*power10(i);
            if(!x)res-=power10(i);
        }
        //第二大类
        if(num[i]==x)res+=get(num, i-1, 0)+1;
        else if(num[i]>x)res+=power10(i);
    }
    return res;
}

int main(){
    int a,b;
    while(cin>>a>>b, a||b){
        if(a>b)swap(a,b);
        
        for(int i=0;i<10;i++)cout<<count(b,i)-count(a-1,i)<<' ';
        cout<<endl;
    }
    return 0; 
}

##恨7不成妻

https://www.acwing.com/problem/content/1088/

----c++版

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=20, p=1e9+7;

struct F{
    int s0, s1, s2;
}f[N][10][8][8];

int power7[N], power9[N];

int mod(ll x, int y){
    return (x%y+y)%y;//注意正余数
}

void init(){
    for(int i=0; i<=9; i++){
        if(i==7)continue;
        auto &v=f[1][i][i%7][i%7];
        v.s0++;
        v.s1+=i;
        v.s2+=i*i;
    }
    ll power=10;//先把10的幂搞出来
    for(int i=2; i<N; i++, power*=10)
        for(int j=0; j<=9; j++)
        {
            if(j==7)continue;
            for(int a=0; a<7; a++)
                for(int b=0; b<7; b++)
                    for(int k=0; k<=9; k++){
                        if(k==7)continue;
                        auto &v1=f[i][j][a][b], &v2=f[i-1][k][mod(a-j*(power%7), 7)][mod(b-j, 7)];
                        v1.s0 = (v1.s0 + v2.s0)%p;
                        v1.s1 = (v1.s1 + j*(power%p)%p*v2.s0 + v2.s1)%p;
                        v1.s2 = (v1.s2 + j*j*(power%p)%p*(power%p)%p*v2.s0 +
                                 2*j*(power%p)%p*v2.s1%p + 
                                 v2.s2
                        )%p;
                    }
        }
    power7[0] = power9[0] = 1;
    for(int i=1; i<N; i++){
        power7[i]=power7[i-1]*10%7;
        power9[i]=(ll)power9[i-1]*10%p;
    }
    
}

F get(int i, int j, int a, int b){
    int s0=0, s1=0, s2=0;
    for(int x=0; x<7; x++)
        for(int y=0; y<7; y++){
            if(x==a||y==b)continue;
            auto v=f[i][j][x][y];
            s0 = (s0+v.s0)%p;
            s1 = (s1+v.s1)%p;
            s2 = (s2+v.s2)%p;
        }
    return {s0, s1, s2};
}

int dp(ll n){
    if(!n) return 0;
    
    ll backup_n = n%p;
    
    vector<int> nums;
    while(n) nums.push_back(n%10), n/=10;
    
    int res=0;
    ll last_a=0, last_b=0;//前面数，前面数每位数字之和
    for(int i=nums.size()-1; i>=0; i--){
        int x=nums[i];
        for(int j=0; j<x; j++){
            if(j==7)continue;
            int a=mod(-last_a%7*power7[i+1], 7);
            int b=mod(-last_b, 7);
            
            auto v=get(i+1, j, a, b);
            res = (res + 
                (last_a%p)*(last_a%p)%p*power9[i+1]%p*power9[i+1]%p*v.s0%p + 
                2*(last_a%p)%p*power9[i+1]%p*v.s1%p + 
                v.s2
            )%p;
        }
        if(x==7)break;
        last_a=last_a*10+x;
        last_b+=x;
        
        if(!i&& last_a%7 && last_b%7) res = (res+backup_n*backup_n)%p;
    }
    return res;
}

int main(){
    init();
    int T;
    cin>>T;
    while(T--){
        ll l,r;
        cin>>l>>r;
        cout<<mod(dp(r)-dp(l-1), p)<<endl;
    }
    
    return 0;
}