3、树（上篇）
3.1 树与树的表示
什么是树？
层次关系，分层次组织在管理上具有更高的效率!
应用-查找
如何实现有效率的查找？
查找（Searching）： 根据某个给定关键字K ，从集合R中找出关键字与K相同的记录
静态查找：集合中记录是固定的
- 没有插入和删除操作，只有查找
动态查找：集合中记录是动态变化的
- 除查找，还可能发生插入和删除
静态查找
方法1：顺序查找
int SequentialSearch (StaticTable *Tbl,
ElementType K)
{ /*在表Tbl[1]~Tbl[n]中查找关键字为K的数据元素*/
int i;
Tbl->Element[0] = K; /*建立哨兵*/
for(i = Tbl->Length; Tbl->Element[i]!= K; i--);
return i; /*查找成功返回所在单元下标；不成功返回0*/
}
顺序查找算法的时间复杂度为O(n)。
方法2：二分查找（Binary Search)
假设n个数据元素的关键字满足有序（比如：小到大）并且是连续存放（数组），那么可以进行二分查找。
[例] 假设有13个数据元素，按关键字由小到大顺序存放，二分查找关健字为444的数据元素过程如下：
1、left = 1, right = 13; mid = (1+13)/2 = 7: 100 < 444;
2、left = mid+1=8, right = 13; mid = (8+13)/2 = 10: 321 < 444;
3、left = mid+1=11, right = 13; mid = (11+13)/2 = 12: 查找结束;
[例] 仍然以上面13个数据元素构成的有序线性表为例，二分查找关健字为 43 的数据元素如下：
1、left = 1, right = 13; mid = (1+13)/2 = 7: 100 > 43;
2、 left = 1, right = mid-1= 6; mid = (1+6)/2 = 3: 39 < 43;
3、left = mid+1=4, right = 6; mid = (4+6)/2 = 5: 51 > 43;
4、left = 4, right = mid-1= 4; mid = (4+4)/2 = 4: 45 > 43;
5、left = 4, right = mid-1= 3; left > right ? 查找失败，结束;
二分查找算法
int BinarySearch ( StaticTable * Tbl, ElementType K)
{ /*在表Tbl中查找关键字为K的数据元素*/
int left, right, mid, NoFound=-1;
left = 1; /*初始左边界*/
right = Tbl->Length; /*初始右边界*/
while ( left <= right )
{
mid = (left+right)/2; /*计算中间元素坐标*/
if( K < Tbl->Element[mid]) right = mid-1; /*调整右边界*/
else if( K > Tbl->Element[mid]) left = mid+1; /*调整左边界*/
else return mid; /*查找成功，返回数据元素的下标*/
}
return NotFound; /*查找不成功，返回-1*/
}
二分查找算法具有对数的时间复杂度O(logN)
二分查找判定树
11个元素的二分查找判定树
树的定义
树（Tree）: n（n≥0）个结点构成的有限集合。
当n=0时，称为空树；
对于任一棵非空树（n> 0），它具备以下性质：
- 树中有一个称为“根（Root）”的特殊结点，用 r 表示；
- 其余结点可分为m(m>0)个互不相交的有限集T1，T2，… ，Tm，其中每个集合本身又是一棵树，称为原来树的“子树（SubTree）”
树与非树?
树的基本术语
1.结点的度（Degree）：结点的子树个数
2.树的度：树的所有结点中最大的度数
3.叶结点（Leaf）：度为0的结点
4.父结点（Parent）：有子树的结点是其子树的根结点的父结点
5.子结点（Child）：若A结点是B结点的父结点，则称B结点是A结点的子结点；子结点也称孩子结点。
6.兄弟结点（Sibling）：具有同一父结点的各结点彼此是兄弟结点。7.路径和路径长度：从结点n1到nk的路径为一个结点序列n1 , n2 ,… , nk , ni是 ni+1的父结点。路径所包含边的个数为路径的长度。
9. 祖先结点(Ancestor)：沿树根到某一结点路径上的所有结点都是这个结点的祖先结点。
10. 子孙结点(Descendant)：某一结点的子树中的所有结点是这个结点的子孙。
11. 结点的层次（Level）：规定根结点在1层，其它任一结点的层数是其父结点的层数加1。
12. 树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度。
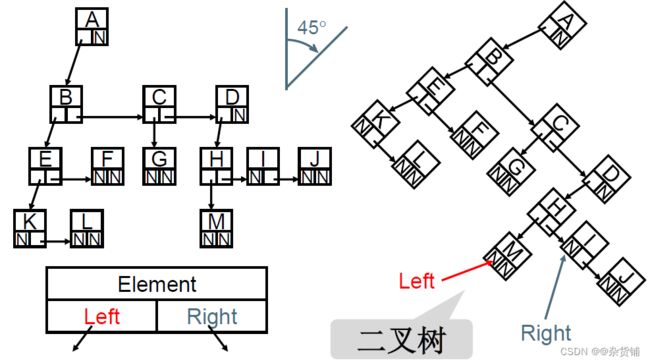
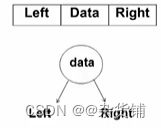
树的表示
因为树的子节点不是统一的，有的只有1个子节点，例如C、H；有的有两个子节点，例如B、E；有的有3个子节点，例如A、D。所以如果按最大子节点数来统一确定节点结构体，会造成空间浪费。
树的表示
进而采取一种“儿子兄弟表示法”，节点结构统一为如下：首先创建一个根节点，令其FristChild指向左边第一颗树T1，再让T1的NextSibling指向其右边第二棵树T2，再令T2的NextSibling指向T3，依次类推，直到把所有的树都串再一起。
儿子兄弟表示法
演变成 二叉树：
typedef struct TNode *Position;
typedef Position BinTree; /* 二叉树类型 */
struct TNode{ /* 树结点定义 */
ElementType Data; /* 结点数据 */
BinTree Left; /* 指向左子树 */
BinTree Right; /* 指向右子树 */
};
3.2 二叉树及存储结构
二叉树的定义
二叉树T：一个有穷的结点集合。这个集合可以为空，若不为空，则它是由根结点和称为其左子树TL和右子树TR的两个不相交的二叉树组成。
二叉树具体五种基本形态：
二叉树的子树有左右顺序之分：
特殊二叉树：
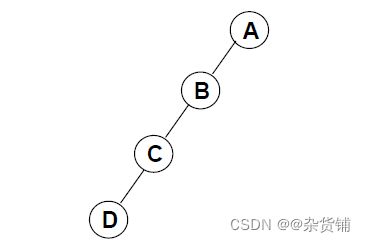
斜二叉树(Skewed Binary Tree)
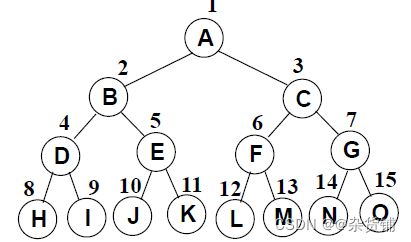
完美二叉树(Perfect Binary Tree) / 满二叉树(Full Binary Tree）
完全二叉树(Complete Binary Tree)
- 有n个结点的二叉树，对树中结点按从上至下、从左到右顺序进行编号，编号为i（1 ≤ i ≤ n）结点与满二叉树中编号为 i 结点在二叉树中位置相同
完全二叉树
非完全二叉树
二叉树重要性质
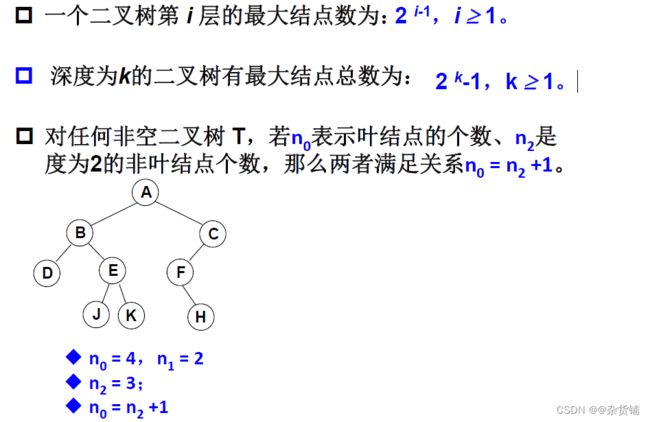
二叉树几个重要性质
二叉树的抽象数据类型定义
类型名称：二叉树
数据对象集：一个有穷的结点集合。 若不为空，则由根结点和其左、右二叉子树组成。
操作集： BT属于 BinTree, Item 属于 ElementType，重要操作有：
1、Boolean IsEmpty( BinTree BT )： 判别BT是否为空；
2、void Traversal( BinTree BT )：遍历，按某顺序访问每个结点；
3、BinTree CreatBinTree( )：创建一个二叉树。
常用的遍历方法有：
void PreOrderTraversal( BinTree BT )：先序----根、左子树、右子树；
void InOrderTraversal( BinTree BT )： 中序---左子树、根、右子树；
void PostOrderTraversal( BinTree BT )：后序---左子树、右子树、根
void LevelOrderTraversal( BinTree BT )：层次遍历，从上到下、从左到右
二叉树的存储结构
1. 顺序存储结构
完全二叉树：按从上至下、从左到右顺序存储
n个结点的完全二叉树的结点父子关系：
一般二叉树：也可以采用这种结构，但会造成空间浪费……
2. 链表存储
typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode{
ElementType Data;
BinTree Left;
BinTree Right;
}
二叉树链式结构
3.3 二叉树的遍历
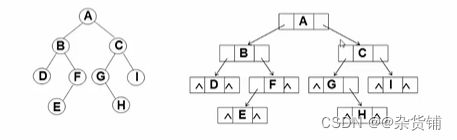
1. 先序遍历
先序遍历
遍历过程为：A（B D F E ）（C G H I）
① 访问根结点；
② 先序遍历其左子树；
③ 先序遍历其右子树。
先序遍历=> A B D F E C G H I
void PreOrderTraversal( BinTree BT )
{
if( BT ) {
printf(“%d”, BT->Data);
PreOrderTraversal( BT->Left );
PreOrderTraversal( BT->Right );
}
}
2. 中序遍历
中序遍历
遍历过程为：（D B E F） A （G H C I）
① 中序遍历其左子树；
② 访问根结点；
③ 中序遍历其右子树。
中序遍历=> D B E F A G H C I
void InOrderTraversal( BinTree BT )
{
if( BT ) {
InOrderTraversal( BT->Left );
printf(“%d”, BT->Data);
InOrderTraversal( BT->Right );
}
}
3. 后序遍历
后序遍历
遍历过程为：（D E F B ）（ H G I C） A
① 后序遍历其左子树；
② 后序遍历其右子树；
③ 访问根结点。
后序遍历=> D E F B H G I C A
void PostOrderTraversal( BinTree BT )
{
if( BT ) {
PostOrderTraversal( BT->Left );
PostOrderTraversal( BT->Right);
printf(“%d”, BT->Data);
}
}
小结
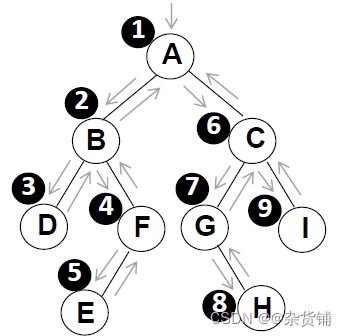
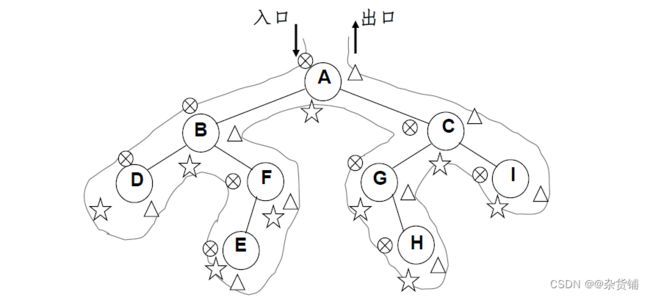
先序、中序和后序遍历过程：遍历过程中经过结点的路线一样，只是访问各结点的时机不同。
图中在从入口到出口的曲线上用⚪×、☆ 和三种符号分别标记出了先序、中序和后序访问各结点的时刻：
3.3.1 二叉树的非递归遍历
1. 中序遍历非递归遍历算法
非递归算法实现的基本思路：使用堆栈
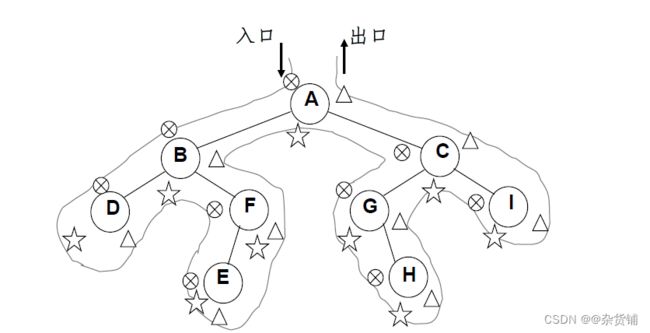
→ 遇到一个结点，就把它压栈，并去遍历它的左子树；
→ 当左子树遍历结束后，从栈顶弹出这个结点并访问它；
→ 然后按其右指针再去中序遍历该结点的右子树。
void InOrderTraversal( BinTree BT )
{ BinTree T=BT;
Stack S = CreatStack( MaxSize ); /*创建并初始化堆栈S*/
while( T || !IsEmpty(S) )
{
while(T)
{ /*一直向左并将沿途结点压入堆栈*/
Push(S,T);
T = T->Left;
}
if(!IsEmpty(S))
{
T = Pop(S); /*结点弹出堆栈*/
printf(“%5d”, T->Data); /*（访问）打印结点*/
T = T->Right; /*转向右子树*/
}
}
}
2. 先序遍历的非递归遍历算法
3. 后序遍历非递归遍历算法
4. 层序遍历
二叉树遍历的核心问题：二维结构的线性化
→从结点访问其左、右儿子结点
→访问左儿子后，右儿子结点怎么办？
- 需要一个存储结构保存暂时不访问的结点
- 存储结构：堆栈、队列
4.1. 队列实现
队列实现：遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点出队、访问该结点、其左右儿子入队
层序基本过程：先根结点入队，然后：
- 从队列中取出一个元素；
- 访问该元素所指结点；
- 若该元素所指结点的左、右孩子结点非空，则将其左、右孩子的指针顺序入队。
void LevelOrderTraversal ( BinTree BT )
{ Queue Q; BinTree T;
if ( !BT ) return; /* 若是空树则直接返回 */
Q = CreatQueue( MaxSize ); /*创建并初始化队列Q*/
AddQ( Q, BT );
while ( !IsEmptyQ( Q ) )
{
T = DeleteQ( Q );
printf(“%d\n”, T->Data); /*访问取出队列的结点*/
if ( T->Left ) AddQ( Q, T->Left );
if ( T->Right ) AddQ( Q, T->Right );
}
}
【例】遍历二叉树的应用：输出二叉树中的叶子结点。
在二叉树的遍历算法中增加检测结点的“左右子树是否都为空”。
//先序二叉树改造
void PreOrderPrintLeaves( BinTree BT )
{
if( BT )
{
if ( !BT-Left && !BT->Right )
printf(“%d”, BT->Data );
PreOrderPrintLeaves ( BT->Left );
PreOrderPrintLeaves ( BT->Right );
}
}
【例】求二叉树的高度。
//后序二叉树改造
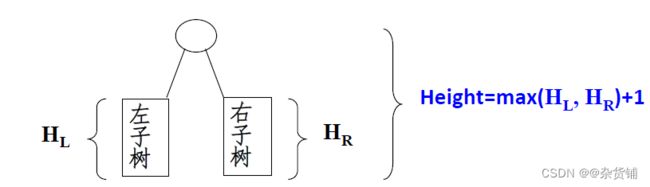
int PostOrderGetHeight( BinTree BT )
{ int HL, HR, MaxH;
if( BT )
{
HL = PostOrderGetHeight(BT->Left); /*求左子树的深度*/
HR = PostOrderGetHeight(BT->Right); /*求右子树的深度*/
MaxH = （HL > HR）? HL : HR; /*取左右子树较大的深度*/
return ( MaxH + 1 ); /*返回树的深度*/
}
else return 0; /* 空树深度为0 */
}
【例】 二元运算表达式树及其遍历
【例】 由两种遍历序列确定二叉树
【例】先序和中序遍历序列来确定一棵二叉树
〖分析〗
根据先序遍历序列第一个结点确定根结点；
根据根结点在中序遍历序列中分割出左右两个子序列
对左子树和右子树分别递归使用相同的方法继续分解。
类似地，后序和中序遍历序列也可以确定一棵二叉树。
3.4 练习-树的同构
题目
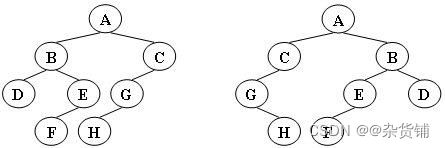
【题】给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。
现给定两棵树，请你判断它们是否是同构的。
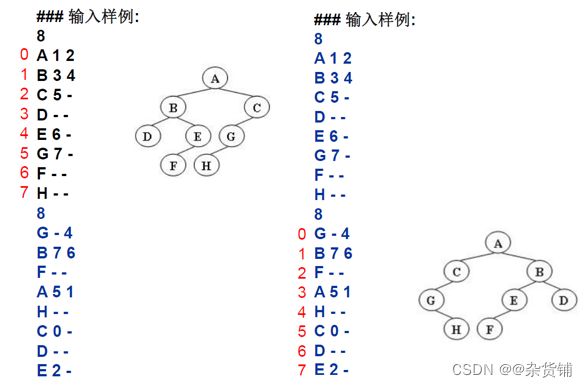
是
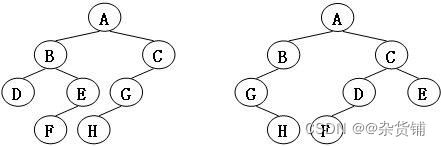否
【分析】
输入格式: 输入给出2棵二叉树的信息：
- 先在一行中给出该树的结点数，随后N行
- 第i行对应编号第i个结点，给出该结点中存储的字母、其左孩子结点的编号、右孩子结点的编号。
- 如果孩子结点为空，则在相应位置上给出“-”。
【求解思路】
- 二叉树表示
- 建二叉树
- 同构判别
二叉树表示
结构数组表示二叉树：静态链表
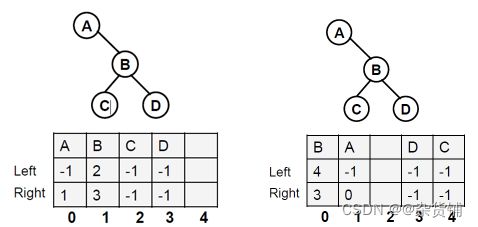
第一行：表示节点
第二行：左儿子的位置，如果没有用-1；
第三行：右儿子的位置，如果没有用-1；
节点不一定从根节点开始，可以任意节点开始。
#define MaxTree 10
#define ElementType char
#define Tree int
#define Null -1
struct TreeNode
{
ElementType Element;
Tree Left;
Tree Right;
} T1[MaxTree], T2[MaxTree];
程序框架搭建
代码实现
（1）Tree BuildTree( struct TreeNode T[] )
//输入二叉树
Tree BuildTree( struct TreeNode T[] )
{ …..
//先确定要输入的节点个数
scanf("%d\n", &N);
if (N)
{
//用check[]数组标记是否被指向,用以找出根节点
for (i=0; i<N; i++) check[i] = 0;
for (i=0; i<N; i++)
{
//循环读入每个节点、左右子节点位置
scanf("%c %c %c\n", &T[i].Element, &cl, &cr);
//如果左节点不为负
if (cl != '-')
{
T[i].Left = cl-'0';
check[T[i].Left] = 1;
}
//左节点为负
else T[i].Left = Null;
//右节点也是同样处理
…….. /*对cr的对应处理 */
}
//循环找出根节点
for (i=0; i<N; i++)
if (!check[i]) break;
Root = i;
}
return Root;
}
//判别两二叉树同构
（2）Isomorphic ( Tree R1, Tree R2 )
int Isomorphic ( Tree R1, Tree R2 )
{
if ( (R1==Null )&& (R2==Null) ) /* both empty */
return 1;
if ( ((R1==Null)&&(R2!=Null)) || ((R1!=Null)&&(R2==Null)) )
return 0; /* one of them is empty */
if ( T1[R1].Element != T2[R2].Element )
return 0; /* roots are different */
if ( ( T1[R1].Left == Null )&&( T2[R2].Left == Null ) )
/* both have no left subtree */
return Isomorphic( T1[R1].Right, T2[R2].Right );
if ( ((T1[R1].Left!=Null)&&(T2[R2].Left!=Null))&&
((T1[T1[R1].Left].Element)==(T2[T2[R2].Left].Element)) )
/* no need to swap the left and the right */
return ( Isomorphic( T1[R1].Left, T2[R2].Left ) &&
Isomorphic( T1[R1].Right, T2[R2].Right ) );
else /* need to swap the left and the right */
return ( Isomorphic( T1[R1].Left, T2[R2].Right) &&
Isomorphic( T1[R1].Right, T2[R2].Left ) );
}