数位DP.

---

度的数量

求给定区间 [X,Y] 中满足下列条件的整数个数：这个数恰好等于 K 个互不相等的 B 的整数次幂之和。

例如，设 X=15,Y=20,K=2,B=2，则有且仅有下列三个数满足题意：

17=2⁴+2⁰
18=2⁴+2¹
20=2⁴+2²

输入格式
第一行包含两个整数 X 和 Y，接下来两行包含整数 K 和 B。

输出格式
只包含一个整数，表示满足条件的数的个数。

数据范围
1 ≤ X ≤ Y ≤ 231 − 1,
1 ≤ K ≤ 20,
2 ≤ B ≤ 10

输入样例：

15 20
2
2

输出样例：

3

#include 
#include 
using namespace std;
const int N = 35; // 位数 
int k, b;
int f[N][N]; // 从前i个数中选j个数的方案数，既组合数 
// 预处理组合数 
void init()
{
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j <= i; j ++ ) 
            if (!j) f[i][j] = 1;
            else f[i][j] = f[i - 1][j] + f[i - 1][j - 1]; 
}
// 求0到n区间中满足条件数的个数
// 条件：数字的B进制表示中，其中K位是1，其余是0 
int dp(int n)
{
    if (n == 0) return 0;
    vector<int> nums; // 存n在B进制下的每一位
    // 把n在B进制下的每一位单独拿出来
    while (n) nums.push_back(n % b), n /= b;
    int res = 0;
    // 右边分支往下走的时候保存前面的信息 
    // 记录之前已经使用的1的个数，当前可以使用的1的个数就是K-last 
    int last = 0;
    // 从最高位开始，遍历每一位 
    for (int i = nums.size() - 1; i >= 0; i -- ) {
        int x = nums[i];
        if (x > 0) { // 只有x>0才可以讨论左右分支 
            //当前位填0，从剩下的所有位（共有i位）中选K-last个数。
            //对应于：左分支中0的情况，合法
            res += f[i][k - last];//i个数中选K-last个数的组合数是多少，选出来这些位填1，其他位填0
            if (x > 1) {
                //当前位填1，从剩下的所有位（共有i位）中选K-last-1个数。
                //对应于：左分支中填1的情况，合法
                if (k - last - 1 >= 0) res += f[i][k - last - 1];//i个数中选K-last-1个数填1的组合数是多少
                //对应于：左分支中其他情况（填大于1的数）和此时右分支的情况（右侧此时也>1），不合法！！！直接break。
                break;
            } else {
                last ++ ;
                //如果已经填的个数last > 需要填的个数K，不合法break
                if (last > k) break;
            }
        } 
        //上面处理完了这棵树的所有左分支，就剩下最后一种右分支的情况
        // 也就是遍历到最后1位，在vector中就是下标为0的地方：i==0；
        // 并且最后1位取0，才算作一种情况res++。因为最后1位不为0的话，已经被上面的ifelse处理了。
        if (i == 0 && last == k) res ++ ;
    } 
    return res; 
}
int main()
{
    init();
    int l, r;
    cin >> l >> r >> k >> b; 
    cout << dp(r) - dp(l - 1) << endl;
    return 0;
}

---

数字游戏

科协里最近很流行数字游戏。

某人命名了一种不降数，这种数字必须满足从左到右各位数字呈非下降关系，如 123，446。

现在大家决定玩一个游戏，指定一个整数闭区间 [a,b]，问这个区间内有多少个不降数。

输入格式
输入包含多组测试数据。

每组数据占一行，包含两个整数 a 和 b。

输出格式
每行给出一组测试数据的答案，即 [a,b] 之间有多少不降数。

数据范围
1 ≤ a ≤ b ≤ 2³¹−1

输入样例：

1 9
1 19

输出样例：

9
18

#include 
#include 
using namespace std;
const int N = 15;    
int f[N][N]; // 最高位是j，且一共有i位不降数的集合 
void init()
{
    for (int i = 0; i <= 9; i ++ ) f[1][i] = 1;
    for (int i = 2; i < N; i ++ )
        for (int j = 0; j <= 9; j ++ )
            for (int k = j; k <= 9; k ++ ) // 枚举下一位 状态划分 
                f[i][j] += f[i - 1][k];  
}
int dp(int n)
{
    if (!n) return 1;

    vector<int> nums;
    while (n) nums.push_back(n % 10), n /= 10;

    int res = 0;
    int last = 0;

    for (int i = nums.size() - 1; i >= 0; i -- ) {
        int x = nums[i];
        for (int j = last; j < x; j ++ )
            res += f[i + 1][j];

        if (x < last) break;
        last = x;

        if (!i) res ++ ;
    }

    return res; 
}
int main()
{
    init();
    int l, r;
    while (cin >> l >> r) 
        cout << dp(r) - dp(l - 1) << endl;
    return 0;
}

笔记学习：
作者：灰之魔女
链接：https://www.acwing.com/solution/content/33446/
来源：AcWing

---

Windy数

Windy 定义了一种 Windy 数：不含前导零且相邻两个数字之差至少为 2 的正整数被称为 Windy 数。

Windy 想知道，在 A 和 B 之间，包括 A 和 B，总共有多少个 Windy 数？

输入格式
共一行，包含两个整数 A 和 B。

输出格式
输出一个整数，表示答案。

数据范围
1 ≤ A ≤ B ≤ 2 × 109

输入样例1：

1 10

输出样例1：

9

输入样例2：

25 50

输出样例2：

20

数位Dp
假设我们当前枚举到第 i 位(设共有 n 位)，且第 i 位上的数字为 x，那么对于答案中第 i 位数字 j 来说，有两类：

1. 0 ~ x-1 (如果第 i 位是最高位，这里是1 ~ x-1)
   括号中提到的1 ~ x-1后面会解释 ,我们用last记录上一位的数字，然后枚举 j ，如果 abs(j-last) >= 2 就累加答案，res += f[i+1][j];
2. x
   不需要枚举j，last = x,再枚举之后的数位即可

上述做完之后，由于上面的答案都是 n 位的，对于数位个数低于 n 的，再累加到答案中就行了

f数组的处理
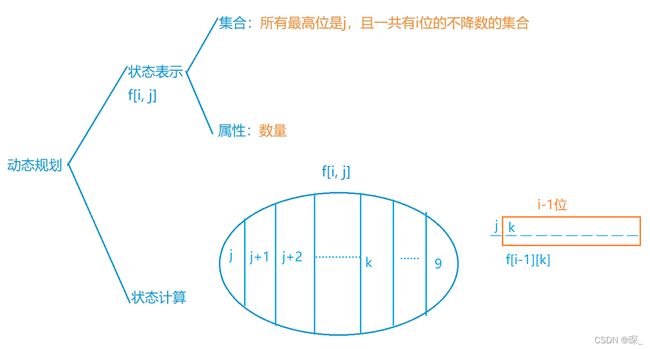
f[i][j] 表示一共有 i 位，且最高位数字为 j 的满足windy数定义的数的个数

状态转移： 因为第 i 位是 j 已经确定，考虑第 i-1 位，设第 i-1 位数字为 k，那么根据windy数定义只要abs(k-j) >= 2就可以转移过来

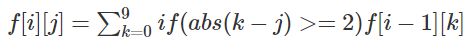
关于前导0
上面提到了枚举的第 i 位是最高位，那么不能填 0，这里解释一下，如果我们填 0，那么答案就会加上f[i+1][0]，举这样一个例子，
对于数字13，他是满足windy数定义的，那么加上前导0之后的013就不会被f[3][0]加进去，原因就是abs(0-1)<2，这样就导致答案漏掉。

#include 
#include 
using namespace std;
const int N = 11;
int f[N][N]; // 表示一共有i位，且最高位数字为j的满足windy数定义的数的个数
void init()
{
    for (int i = 1; i <= 9; i ++ ) f[1][i] = 1; 
    for (int i = 2; i < N; i ++ )
        for (int j = 0; j <= 9; j ++ ) 
            for (int k = 0; k <= 9; k ++ )
                if(abs(j - k) >= 2)
                    f[i][j] += f[i - 1][k];
}
int dp(int n)
{
    if (!n) return 0;

    vector<int> nums; 
    while (n) nums.push_back(n % 10), n /= 10;

    int res = 0;
    int last = -2;
    for (int i = nums.size() - 1; i >= 0; i -- ) { // 从高位到低位 
        int x = nums[i];

        // 0/1 ~ X-1
        for (int j = i == nums.size() - 1; j < x; j ++ ) // i==nums.size()-1 最高位从1开始 
            if (abs(j - last) >= 2)
                res += f[i + 1][j];

        // X
        if (abs(x - last) >= 2) last = x;
        else break;

        if (!i) res ++ ;
    }

    // 特殊处理有前导0的数，答案小于nums.size()位的 
    for (int i = 1; i < nums.size(); i ++ )
        for (int j = 1; j <= 9; j ++ )
            res += f[i][j]; 

    return res; 
}
int main()
{
    init();
    int l, r;
    cin >> l >> r; 
    cout << dp(r) - dp(l - 1) << endl;
    return 0;
}

笔记学习：
作者：Moon_light
链接：https://www.acwing.com/solution/content/15562/
来源：AcWing

---

数字游戏 II

由于科协里最近真的很流行数字游戏。

某人又命名了一种取模数，这种数字必须满足各位数字之和 mod N 为 0。

现在大家又要玩游戏了，指定一个整数闭区间 [a.b]，问这个区间内有多少个取模数。

输入格式
输入包含多组测试数据，每组数据占一行。

每组数据包含三个整数 a,b,N。

输出格式
对于每个测试数据输出一行结果，表示区间内各位数字和 mod N 为 0 的数的个数。

数据范围
1 ≤ a,b ≤ 2³¹−1,
1 ≤ N < 100

输入样例：

1 19 9

** 输出样例：**

2

数位DP
在几道数位Dp题目练习过后，这类题目重点在于找到左边那一类如何直接计算
对于这一题来说，假设我们当前枚举到的第i位，且第i位上的数字是x，那么对于答案中的第i位数字j来说，可以填两类数：

1. 0~x-1
   我们用last表示到当前为止，前面数位上的数字之和，对此，当前第i位数字为j，前面数字之和为last，那么
   后i位(包括j这一位)数字之和sum与last的关系就是(last+sum)%N == 0,那么sum%N的结果等价于(-last)%N,
   所以res += f[i+1][j][(-last%N)]; (后面会提到f数组的处理)
2. x
   如果j填x，那么不用枚举了，last += x，再枚举下一位即可

f数组的处理
f[i][j][k] 表示一共有i位，且最高位数字是j，且所有位数字和模N结果为k的数的个数

状态转移： 因为第i位已经是j，且所有数字之和模N为k，所以我们考虑第i-1位，假设第i-1位数字是x，由于j已经知道，
那么剩下的i-1位数字之和模N的结果就是(k-j)%N，那么状态转移方程就是：

#include 
#include 
#include 
#include 
using namespace std;
const int N = 15, M = 110;
int p;
int f[N][10][M]; 
int mod(int x, int y)
{
    return (x % y + y) % y;
}
void init()
{
    memset(f, 0, sizeof f);
    for (int i = 0; i <= 9; i ++ ) f[1][i][i % p] ++ ;
    for (int i = 2; i < N; i ++ )
        for (int j = 0; j <= 9; j ++ )
            for (int k = 0; k < p; k ++ )
                for (int x = 0; x <= 9; x ++ ) 
                    f[i][j][k] += f[i - 1][x][mod(k - j, p)];
}
int dp(int n)
{
    if (!n) return 1;
    vector<int> nums; 
    while (n) nums.push_back(n % 10), n /= 10;
    int res = 0;
    int last = 0;
    for (int i = nums.size() - 1; i >= 0; i -- ) {
        int x = nums[i];
        for (int j = 0; j < x; j ++ )
            res += f[i + 1][j][mod( - last, p)];
        last += x;
        if (!i && last % p == 0) res ++ ;
    } 
    return res; 
}
int main()
{
    int l, r;
    while (cin >> l >> r >> p) {
        init();
        cout << dp(r) - dp(l - 1) << endl;
    }
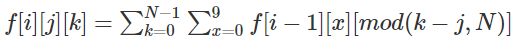
    return 0;
}

笔记学习：
作者：Moon_light
链接：https://www.acwing.com/solution/content/15556/
来源：AcWing

---

不要62

杭州人称那些傻乎乎粘嗒嗒的人为 62（音：laoer）。

杭州交通管理局经常会扩充一些的士车牌照，新近出来一个好消息，以后上牌照，不再含有不吉利的数字了，这样一来，就可以消除个别的士司机和乘客的心理障碍，更安全地服务大众。

不吉利的数字为所有含有 4 或 62 的号码。例如：62315,73418,88914 都属于不吉利号码。但是，61152 虽然含有 6 和 2，但不是 连号，所以不属于不吉利数字之列。

你的任务是，对于每次给出的一个牌照号区间 [n,m]，推断出交管局今后又要实际上给多少辆新的士车上牌照了。

输入格式
输入包含多组测试数据，每组数据占一行。

每组数据包含一个整数对 n 和 m。

当输入一行为“0 0”时，表示输入结束。

输出格式
对于每个整数对，输出一个不含有不吉利数字的统计个数，该数值占一行位置。

数据范围
1 ≤ n ≤ m ≤ 109

输入样例：

1 100
0 0

输出样例：

80

数位DP基本概念+数位DP记忆化搜索

本题参数 st 需要记录的参数是：前一位数字是什么

这样就能有效 排除 枚举 62 的情况，而枚举 4 的情况直接 特判 即可

#include 
#include 
#include 
#include 
using namespace std;
const int N = 35;
int f[N][10];
void init()
{
    for (int i = 0; i <= 9; i ++ )
        if (i != 4)
            f[1][i] = 1;
    for (int i = 1; i < N; i ++ )
        for (int j = 0; j <= 9; j ++ ) {
            if (j == 4) continue;
            for (int k = 0; k <= 9; k ++ ) {
                if (k == 4 || j == 6 && k == 2) continue;
                f[i][j] += f[i - 1][k];
            }
        }
}
int dp(int n)
{
    if (!n) return 1;

    vector<int> nums;
    while (n) nums.push_back(n % 10), n /= 10;

    int res = 0;
    int last = 0;
    for (int i = nums.size() - 1; i >= 0; i -- ) {
        int x = nums[i];
        for (int j = 0; j < x; j ++ ) {
            if (j == 4 || last == 6 && j == 2) continue;
            res += f[i + 1][j];
        }

        if (x == 4 || last == 6 && x == 2) break;
        last = x;

        if (!i) res ++ ;
    }

    return res;
}
int main()
{
    init();
    int l, r;
    while (cin >> l >> r, l || r) {
        cout << dp(r) - dp(l - 1) << endl;  
    }
    return 0; 
} 

---

恨7不成妻

单身！

依然单身！

吉哥依然单身！

DS 级码农吉哥依然单身！

所以，他平生最恨情人节，不管是 214 还是 77，他都讨厌！

吉哥观察了 214 和 77 这两个数，发现：

2+1+4=7
7+7=7×2
77=7×11
最终，他发现原来这一切归根到底都是因为和 7 有关！

所以，他现在甚至讨厌一切和 7 有关的数！

什么样的数和 7 有关呢？

如果一个整数符合下面三个条件之一，那么我们就说这个整数和 7 有关：

整数中某一位是 7；
整数的每一位加起来的和是 7 的整数倍；
这个整数是 7 的整数倍。
现在问题来了：吉哥想知道在一定区间内和 7 无关的整数的平方和。

输入格式
第一行包含整数 T，表示共有 T 组测试数据。

每组数据占一行，包含两个整数 L 和 R。

输出格式
对于每组数据，请计算 [L,R] 中和 7 无关的数字的平方和，并将结果对 109+7 取模后输出。

数据范围
1 ≤ T ≤ 50,
1 ≤ L ≤ R ≤ 1018

输入样例：

3
1 9
10 11
17 17

输出样例：

236
221
0

---