数字图像处理——第十一章 表示和描述
文章目录
- 引言
- 11.1 表示
-
- 11.1 边界追踪
- 11.2 链码
- 11.3 多边形近似
- 11.4 聚合和分裂技术
- 11.5 标记图
- 11.1.6 边界线段
- 11.2 边界描绘子
-
- 11.2.1 基础描绘子
- 11.2.2 形状数
- 11.2.3 傅里叶描绘子
- 11.2.4 统计距
- 11.3 区域描绘子
-
- 11.3.1 简单区域描绘子
- 11.3.2 拓扑描述子
- 11.3.3 纹理
- 11.3.4 不变矩
- 11.4 使用主成分进行描述
- 实验部分
- 总结
引言
继上一章将图像分割成多个区域后,分割的像素集可以分为外部特征(边界)和内部特征(区域),本章的任务是基于所选择的来表示描述区域。如,区域可由其边界表示,边界可用特征对其描述,选择用来作为描绘子的特征应尽可能地对大小、平移和旋转不敏感。
表示部分:边界表示
描述部分:边界描述、区域描述、关系描述、主分量描述
11.1 表示
边界表示:
主要分2个阶段:边界追踪(轮廓提取)、基于特定目标(精确/方便/高效)的边界表示。
边界追踪部分主要介绍Moore算法;边界表示部分主要介绍Freeman链码、边界的多边形近似、标记图、边界线段和骨架。
11.1 边界追踪
边界追踪算法也称为Moore边界追踪算法。要求一个区域边界上的点以顺或逆时针方向排序。
我们假设:
- 处理的是二值图像(但边界未知),其目标和背景点分别标为1和0;
- 图像使用值为0的边界填充,因为消除了目标和图像边界合并的可能性。
Moore算法:
step1: 找到图像左上角为1的点 b 0 b_0 b0为边界起始点。 b 0 b_0 b0左边的点为 c 0 c_0 c0(显然值为0),从 c 0 c_0 c0开始按顺时针方向考察 b 0 b_0 b0的8邻域,找到的第一个值1的点为 b 1 b_1 b1(边界的第2个点),令扫描到 b 1 b_1 b1前的点为 c 1 c_1 c1
step2: 赋值b= b 1 b_1 b1,c= c 1 c_1 c1
step3: 从c开始顺时针扫描b的8邻域,令b的8个邻点为 n 1 , n 2 , n 3 . . . n 8 n_1,n_2,n_3...n_8 n1,n2,n3...n8,找到第一个值1的点 n k n_k nk,其之前的点 n k − 1 n_{k-1} nk−1
step4: 赋值b= n k n_k nk, n k − 1 n_{k-1} nk−1
step5: 重复step3和step4,直到b= b 0 b_0 b0且下一个边界点为 b 1 b_1 b1
注:step5中的停止规则,经常错误得被陈述为再次遇到 b 0 b_0 b0时停止,但如果第一个点存在毛刺则会导致结果的出错,直到b= b 0 b_0 b0且下一个边界点为 b 1 b_1 b1,判断的言外之意是说明 b 0 b_0 b0只有一个邻边界点 b 1 b_1 b1。
11.2 链码
链码被用来顺次连接具有指定长度和方向(逆时针)的直线段来表示边界,这种表示基于线段的4连接或8连接,称为Freeman编码。
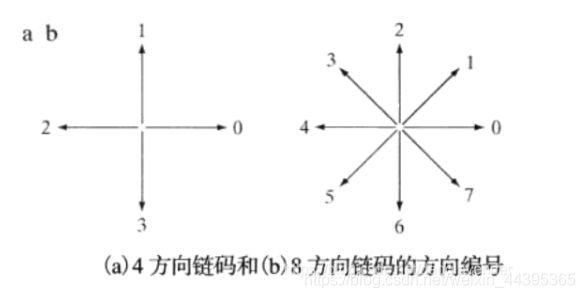
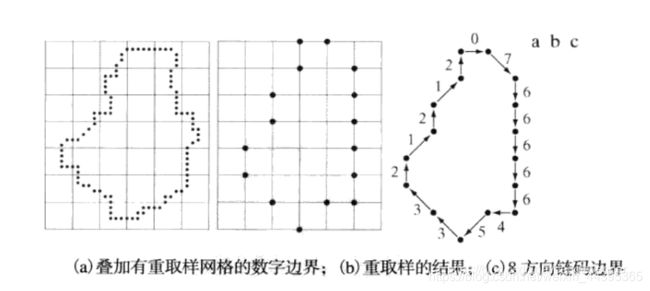
边界的链码取决于起始点,我们可以将链码视为方向号码的一个循环序列,得到号码序列的最小整数值(左边0多)。
也可以使用链码的一次差分来对旋转进行归一化,仅当对旋转和尺度的变化,边界本身不变时,这些归一化才是准确的。
例:8方向链码(下图所示)

我们按照逆时针方向,如2到1 需要7 steps, 来得到差分码,解决旋转归一化的问题。
11.3 多边形近似
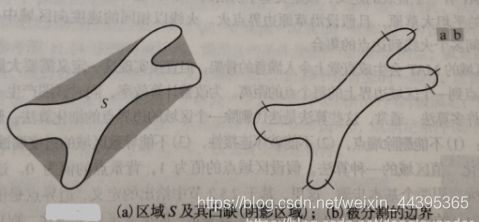
数字边界可以用多边形以任意精度来近似。对一条闭合边界,当多边形的边数等于边界上的点数时,该近似就会很精确,此时每对相邻点定义了多边形的一条边。多边形近似的目的是用尽可能少的线段获取给定边界的基本形状。实际中,很有效的近似技术是用最小周长多边形(MPP)来表示边界。

图三中的黑点是“镜像”凹顶点,目的是用最小周长多边形来近似图形。图三与多边形近似的图形形状相同。
11.4 聚合和分裂技术
11.5 标记图
标记是边界的一维表达,其基本思想是将原始的二维边界用一个一维函数来表示,以达到降低表达难度的作用。
11.1.6 边界线段
当边界线包含一个或多个携带形状信息的明显凹度时,将边界分解为线段是很有用的。差集H-S称为集合S和凸缺D,凸壳是H,分段算法:追踪S的轮廓,并标记进入或离开一个凸缺的转变点,从打标记的位置进行分段。
实际上,由于数字化、噪声和分割变形的影响,导致在边界上有随机散布的无意义的小凸缺,应在处理之前使用平滑或者多边形近似。
11.2 边界描绘子
11.2.1 基础描绘子
-
边界长度:
对于两个方向上以单位间距定义的链码曲线,垂直分量和水平分量的像素数量加上对角分量的像素数量的根号2倍,可给出曲线的准确长度; -
边界直径:
D i a m ( B ) = m a x [ D ( p i , p j ) ] Diam(B)=max[D(p_i,p_j)] Diam(B)=max[D(pi,pj)] p i , p j p_i,p_j pi,pj是边界上的点,直径的值和组成直径的两个端点的直线段的方向是边界的有用描绘子; -
边界的偏心率:
由边界与两个轴(长轴与短轴)相交的4个外部点所组成的方框,称为基本矩形,长轴与短轴之比称为边界的偏心率; -
曲率:
定义为斜率的变化率,近似:用相邻边界线段的斜率差作为这两条线段交点处的曲率。
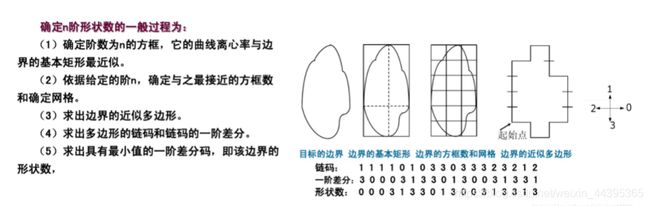
11.2.2 形状数
形状数是基于4链码的边界描述符,形状数定义为最小量级的一次差分,形状数的阶定义为其表示的数字个数。
11.2.3 傅里叶描绘子

上图显示了xy平面的K点数字边界,我们将虚轴和实轴的两个坐标当作一个复数来处理:
s ( k ) = x ( k ) + j y ( k ) s(k)=x(k)+jy(k) s(k)=x(k)+jy(k) 将二维问题简化成了一维问题。
s(k)近似为 s ( k ) = 1 k ∑ u = 0 p − 1 a ( u ) e j 2 π u k P s(k)=\frac{1}{k} \sum_{u=0} ^{p-1} a(u)e^ \frac{j2\pi uk}{P} s(k)=k1u=0∑p−1a(u)ePj2πuk使用前P个傅里叶系数, 其中 a ( u ) = ∑ k = 0 k − 1 s ( k ) e − j 2 π u k K a(u)=\sum_{k=0} ^{k-1} s(k)e^-\frac{j2\pi uk}{K} a(u)=k=0∑k−1s(k)e−Kj2πukk=0,1,2…K-1。高频成分说明精细细节,低频成分决定全局形状,因此P越小,边界丢失的细节就越多。
11.2.4 统计距
边界线段的性质可用统计距来定理描述,如均值、方差和高阶矩。

该函数是这样获得的:先将该线段的两个端点连接起来,然后旋转该直线线段,直到该直线线段称为水平线段。此时,边界线段上的所有点的坐标也旋转相同的角度。
将g的幅度视为一个离散随机变量v,形成幅度直方图 p ( v i ) p(v_i) p(vi),i ∈ \in ∈(0,A-1), p ( v i ) p(v_i) p(vi)是 v i v_i vi出现的概率统计,但n阶矩和均值通常不能区分不同形状的信号。
我们将 g ( r ) g(r) g(r)归一为单位面积,当作直方图来处理。
n 阶 矩 : μ ( v ) = ∑ i = 0 A − 1 ( v i − m ) n p ( v i ) n阶矩:\mu (v)=\sum _{i=0} ^{A-1}(v_i-m)^{n}p(v_i) n阶矩:μ(v)=i=0∑A−1(vi−m)np(vi)
均 值 : m = ∑ i = 0 k − 1 r i g ( r i ) 均值:m=\sum_{i=0} ^{k-1} r_i g(r_i) 均值:m=i=0∑k−1rig(ri) K是边界的点数,n阶矩直接与 g ( r ) g(r) g(r)的性质相关,变量的一阶原始矩等价于数学期望(expectation)、二至四阶中心矩被定义为方差(variance,度量曲线关于r的均值的扩展程度)、偏度(skewness,度量曲线关于均值的对称性)和峰度(kurtosis)。
11.3 区域描绘子
主要讨论区域的纹理描述、不变矩描述和其他简单描述
11.3.1 简单区域描绘子
-
圆形度:
R C = 4 π A P 2 R_C=\frac{4 \pi A}{P^2} RC=P24πA -
致密度
致 密 度 = P 2 A 致密度=\frac{P^2}{A} 致密度=AP2
P为周长,A为面积。 -
灰度值
灰度的均值和中值,最小灰度值和最大灰度值。
11.3.2 拓扑描述子
与距离或基于距离度量概念的任何特性无关,对于图形区域的整体描述是很有用的,与孔洞数量、连通分量的数量、欧拉数有关。
基本元素:

孔洞数量H,连通分量C,可用于定义欧拉数E:
E = C − H (1) E=C-H \tag{1} E=C−H(1) V − Q + F = C − H = E (2) V-Q+F=C-H=E \tag{2} V−Q+F=C−H=E(2) V是顶点数,Q表示边数,F表示面数。

11.3.3 纹理
纹理描述主要有三种方法:统计方法、结构方法、频谱方法。
- 统计方法考察纹理的平滑、粗糙、粒状等特征;
- 结构方法考察纹理的排列描述;处理图像像元的排列;
- 频谱方法考察纹理的周期性。基于傅里叶频谱的特性。
纹理反映像素灰度的空间分布属性,表现为局部不规则但宏观有规律性。
11.3.4 不变矩
根据归一化中心矩可获得7个不变矩,其对同一区域的平移、缩放、旋转、镜像都不敏感。


11.4 使用主成分进行描述
主成分变换,是指由原始图像数据协方差矩阵的特征值和特征向量建立起来的变换核,将光谱特征空间原始数据向量投影到平行于地物集群椭球体各结构轴的主成分方向,突出和保留主要地物类别信息,用来进行图像增强、特征选择和图像压缩的处理方法。
霍特林变换:
y = A ( x − m x ) y=A(x-m_x) y=A(x−mx) m x m_x mx为x的均值,A为特征向量为 C x C_x Cx(正交)作为行向量组成的矩阵,可处理y重建x的问题。
x 1 = A k T y + m x x_1=A_k^ T y+m_x x1=AkTy+mx
均 方 差 e m s = ∑ j = k + 1 n λ j 均方差e_{ms}=\sum _{j=k+1} ^{n} \lambda_j 均方差ems=j=k+1∑nλj若k=n(使用了所有的特征向量),误差为0,由于 λ j \lambda_j λj单调递减,通过选取与最大特征值相对应的k个特征向量,可使得误差最小,霍特林变换为主成分变换,达到最佳效果。
实验部分
- 多边形逼近
img=cv.imread('pic/lunkuo.tif',0)
t1,img_OTSU=cv.threshold(img,0,255, cv.THRESH_OTSU)
# 返回轮廓
contour,hierarchy=cv.findContours(img_OTSU,cv.RETR_LIST,cv.CHAIN_APPROX_SIMPLE)
def approx_img(img,contours,coefficient):
perimeter=coefficient*cv.arcLength(contour[0],True)
approx=cv.approxPolyDP(contour[0],perimeter,True)
img_approx=cv.drawContours(img,[approx],-1,(0,0,255),4)
cv.imshow("coefficient is %.3f "% coefficient, img_approx)
approx_img(img,contour[0],0.002)
approx_img(img,contour[0],0.1)
cv.waitKey(0)
cv.destroyAllWindows()

实验分析:随着系数的减小,多边形将越来越逼近实际图形的形状。
- 链码(代码部分算法设计暂时消化不了)
#主要代码
#寻找起始点
h,w = img_bin.shape
for i in range(h):
for j in range(w):
if (img_bin[i,j] == 255) and (img_bin[i-1,j] == 0):
start_x = i
start_y = j
is_start_point = 1
break
if is_start_point == 1:
break
#(1,39)
#定义链码相对应的增量坐标
neibor = [(0,1),(-1,1),(-1,0),(-1,-1),(0,-1),(1,-1),(1,0),(1,1)]#邻域点
temp = 2#链码值,也是neibor的索引序号,这里是从链码的2号位进行搜索
contours = [(start_x,start_y)]#用于存储轮廓点
#将当前点设为轮廓的开始点
current_x = start_x
current_y = start_y
#temp=2,表示从链码的2方向进行邻域检索,通过当前点和邻域点集以及链码值确定邻域点
neibor_x = current_x + neibor[temp][0]
neibor_y = current_y + neibor[temp][1]
#因为当前点的值为起始点,而终止检索的条件又是这个,所以会产生冲突,因此先寻找第二个边界点
is_contour_point = 0
while is_contour_point == 0: # 邻域点循环,当是目标像素点时跳出
if img_bin[neibor_x, neibor_y] == 255:
# 将符合条件的邻域点设为当前点进行下一次的边界点搜索
current_x = neibor_x
current_y = neibor_y
is_contour_point = 1
contours.append((current_x, current_y))
temp = temp - 2 # 作为下一个边界点的邻域检测起始点,顺时针旋转90度
print(1)
if temp < 0:
temp = len(neibor) + temp
else:
temp = temp + 1 # 逆时针旋转45度进行搜索
if temp >= 8:
temp = temp - len(neibor)
neibor_x = current_x + neibor[temp][0]
neibor_y = current_y + neibor[temp][1]
#开始第三个及以后的边界点的查找
while not((current_x == start_x) and (current_y == start_y)):#轮廓扫描循环
is_contour_point = 0
while is_contour_point == 0:#邻域点循环,当是目标像素点时跳出
if img_bin[neibor_x,neibor_y] == 255:#邻域是白点时,即为边界
#将符合条件的邻域点设为当前点进行下一次的边界点搜索
current_x = neibor_x
current_y = neibor_y
is_contour_point = 1#将判断是否为边界点的标签设置为1,用于跳出循环
contours.append((current_x,current_y))
temp = temp - 2#作为下一个边界点的邻域检测起始点,顺时针旋转90度
if temp < 0:
temp = len(neibor) + temp
else:
temp = temp + 1#逆时针旋转45度进行搜索
if temp >= 8:
temp = temp - len(neibor)
neibor_x = current_x + neibor[temp][0]
neibor_y = current_y + neibor[temp][1]
- 骨架提取
一、fig, ax = plt.subplots()的作用?
它是用来创建 总画布/figure“窗口”的,有figure就可以在上边(或其中一个子网格/subplot上)作图了,(fig:是figure的缩写)。
plt.subplot(111)是plt.subplot(1, 1, 1)另一个写法而已,更完整的写法是plt.subplot(nrows=1, ncols=1, index=1)
fig, ax = plt.subplots()等价于fig, ax = plt.subplots(11)。
fig, axes = plt.subplots(23):即表示一次性在figure上创建成2*3的网格,使用plt.subplot()只能一个一个的添加[引用链接]:
二、骨架提取算法(open cv自带):morphology.skeletonize
三、plt.tight_layout() 作用:自动调整子图参数,使之填充整个图像区域。
四、title:
matplotlib.pyplot.suptitle(
t, # text缩写。即标题文字。
fontsize | size, # 设定字体大小。
x, # 设定标题相对于x轴的位置,默认是’0.5’。
y, # 设定标题相对于y轴的位置,默认是’0.98’。
ha | horizontalalignment, # 和参数x一起使用,设定标题水平方位,默认是‘center’。共3个可选值{‘center’, ‘left’, right’}。
va | verticalalignment, # 和参数y一起使用,设定标题垂直方位, 默认是’top’。共4个可选值{‘top’, ‘center’, ‘bottom’, ‘baseline’}。
fontweight | weight # 设定字体权重。
from skimage import morphology,data,color
import matplotlib.pyplot as plt
image=cv.imread('pic/bear_gray.jpg')
image=1-image
#实施骨架算法
skeleton =morphology.skeletonize(image)
#显示结果
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(8, 4))
ax1.imshow(image,plt.cm.gray)
ax1.axis('off')
ax1.set_title('original', fontsize=20)
ax2.imshow(skeleton, cmap=plt.cm.gray)
ax2.axis('off')
ax2.set_title('skeleton', fontsize=20)
fig.tight_layout()
plt.show()
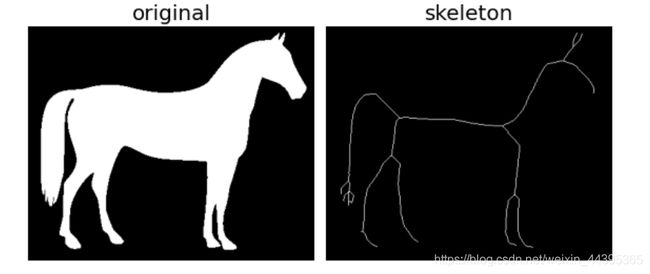
实验分析:目标图形被削减成主要目标主要构成的骨架,但opencv自带的骨架提取函数与原图的形状有一定的偏差,总体轮廓也勾勒得不全。
总结
表示和描述是图像分割之后的重要处理步骤,对于内部和外部特征,计算机都有不同的处理方法,具体选择哪一种方法,取决于所考虑的问题,目的是能够获取描绘子,并同时尽可能保留位置、大小和方向的独立性。