鸢尾花分类
目录
前言:
1.1鸢尾花数据集
1.2原生代码实现鸢尾花分类
1.3keras实现鸢尾花分类
前言:
开源一个学习tensorflow入门级项目——鸢尾花分类;采用两种方式用于实现:一种是采用tensorflow原生代码进行编写,一种是采用keras模块进行编写;采用python3.9+tensorflow2.10,利用pycharm2022进行编译。
1.1鸢尾花数据集
Iris数据集是常用的分类实验数据集,由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集,是一类多重变量分析的数据集。数据集包含150个数据样本,分为3类,每类50个数据,每个数据包含4个属性。可通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa)山鸢尾,(Versicolour)变色鸢尾,(Virginica)维吉尼亚鸢尾三个种类中的哪一类。
1.2原生代码实现鸢尾花分类
采用tensorflow原生代码实现鸢尾花分类,实现过程及代码如下:
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
# 导入数据,分别为输入特征和标签 iris为鸢尾花数据集
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保大家结果一致)
# 实际中打乱数据并不使用随机种子
# 使用相同的seed,保证输入特征和标签一一对应
np.random.seed(116)
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
# tf.cast()数据类型的强制转换
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征,故输入层为4个输入节点;因为3分类,故输出层为3个神经元 (4输入3输出)
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
# tf.Variable()标记参数可训练
# tf.random.truncated_normal() 生成截断式正态分布的随机数
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
# 训练部分
for i in range(epoch): # 数据集级别的循环,每个i循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as g: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # tf.matmul()矩阵乘法 线性模型y=w*x+b
y = tf.nn.softmax(y) # 将张量转换为概率值,让其符合概率分布
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数 即实际值减去模型预测的值平方再求平均
loss_all += loss.numpy() # 将每个step计算出的loss累加
# 计算loss对各个参数的梯度
grads = g.gradient(loss, [w1, b1])
# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad (本质就是SGD)
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b1自更新
# 每循环一轮,就打印一次loss信息
print("Epoch {}, loss: {}".format(i, loss_all))
train_loss_results.append(loss_all)
loss_all = 0 # loss_all归零,为记录下一个epoch循环的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类,横向最大值
# 将pred转换为y_test的数据类型 tf.cast()进行数据类型的强制转换
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
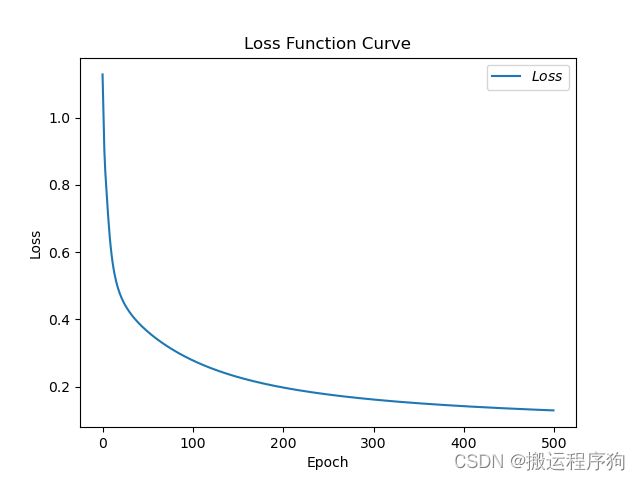
经过运行,得到训练集损失率图像1.1,测试集准确率图像1.2。从图1.1中我们可以看到随着训练轮数的不断增大,损失在不断减小;从图1.2中我们可以看到随着训练轮数的不断增大,测试集准确率不断增大,最后能够达到100%。
图1.1 训练集损失率
图1.2测试集准确率
1.3keras实现鸢尾花分类
调用tensorflow中的keras模块实现鸢尾花分类,实现过程及代码如下:
# 导入相关模块
import tensorflow as tf
from matplotlib import pyplot as plt
from sklearn import datasets
import numpy as np
# 导入输入特征和标签
x_train = datasets.load_iris().data
y_train = datasets.load_iris().target
# 测试集从训练集中按比例划分
# 数据集乱序
np.random.seed(116)
np.random.shuffle(x_train)
np.random.seed(116)
np.random.shuffle(y_train)
tf.random.set_seed(116)
# 搭建网络结构
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(3, activation='softmax')
])
# 配置训练方法
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.1), # 优化器SGD
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
# 分类问题损失函数用交叉熵,因为使用了softmax所以使用False
metrics=['sparse_categorical_accuracy']
# metrics 网络评测指标 当模型输出为概率分布,标签为数值时,metrics用sparse_categorical_accuracy
)
# 执行训练过程
# validation_split 告知训练集的多少比例给测试集
# validation_freq 多少次epoch验证一次结果
history = model.fit(x=x_train, y=y_train, batch_size=32, epochs=500, validation_split=0.2, validation_freq=20)
# 打印网络结构和参数统计
model.summary()
# 显示训练集loss曲线 测试集acc曲线
# history.history可以获得loss和acc数据
loss = history.history['loss']
val_acc = history.history['val_sparse_categorical_accuracy']
plt.plot(loss, label='Training Loss')
plt.title('Training Loss')
plt.legend()
plt.show()
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Validation Accuracy')
plt.legend()
plt.show()通过观察代码,我们可以发现采用keras模块编写的代码要比tensorflow原生代码简洁了很多,这是因为keras是tensorflow重要的集成模块,它将许多操作进行了封装,想要使用的时候直接调用就可以了。
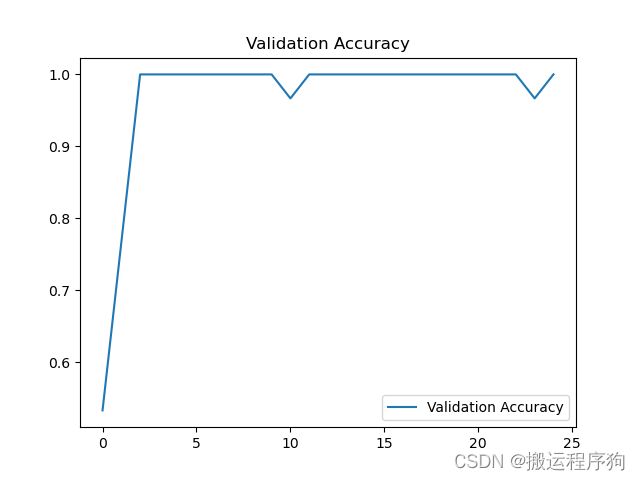
经过运行,得到训练集损失率图像1.3,测试集准确率图像1.4。从图1.3中我们可以看到随着训练轮数的不断增大,损失在不断减小;从图1.4中我们可以看到随着训练轮数的不断增大,测试集准确率不断增大,最后能够达到100%。
图1.3 训练集损失率
图1.4测试集准确率