基于matlab的TOPSIS(优劣距离法)综合评价模型

  C.L.Hwang 和 K.Yoon 于1981年首次提出 TOPSIS  ，可翻译为逼近理想解排序法，国内常简称为优劣解距离法。 TOPSIS 法是一种常用的综合评价方法，能充分利用原始数据的 信息，其结果能精确地反映各评价方案之间的差距。 基本过程为先将原始数据矩阵统一指标类型（一般正向化处理） 得到正向化的矩阵，再对正向化的矩阵进行标准化处理以消除各指 标量纲的影响，并找到有限方案中的最优方案和最劣方案，然后分 别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对 象与最优方案的相对接近程度，以此作为评价优劣的依据。该方法 对数据分布及样本含量没有严格限制，数据计算简单易行。

现在我们用一个引例来简单解释一下TOPSIS的原理。

姓名	数学	体育	犯错次数
小慧	75	89	5
小妍	62	88	3
小欣	82	72	2
小智	92	56	1

现在有4位同学参加竞选，我们需要选出最优秀的学生。这就设计涉及到评价问题，我们需要制定一个合理的评级方法来选出最优秀的学生。我们先观察各个指标。一共有3个指标，分别为数学，体育，和犯错次数。这其中数学，体育肯定是越高越好，而犯错次数次数越少越好。这就涉及到指标的种类，分别为下表所示。

指标类型	特征	举例
极大型指标	越大越好	成绩
极小型指标	越小越好	费用
区间指标	落在一个区间	体温
中间型指标	越接近某个值越好	水质的PH

各个指标的转化方法见下图所示，这里要注意的是方法不止这一种。

 

由于评价指标的好怀标准不一样，例如我们希望极大型指标越大越好，而希望中间型指标越靠近理想值，所以我们需要将所有指标正向化，即通过一定转换使每一个指标都是越大越好，这样我们就统一了评价标准。

接下来我们要考虑的一个问题就是，我们指标的量纲不一样，会导致我们的结果对某个指标不灵敏。例如身高（厘米cm）和犯错次数就相差两个数量级，这就会导致一个情况，犯错次数对我们评价的结果影响十分小，犯错次数指标就失去了意义。所以在综合评价之前，我们先进行指标标准化。指标标准化方法见下图所示，这里要注意的是方法不止这一种。

 现在到了最后的环节了，计算得分。如何计算得分呢？这里我们已经将所有的数据进行了正向标准化，数据越大，得分肯定越高。

这里我们定义：

得分=数据与最小值的距离/(数据与最小值的距离+数据与最大值的距离)

为保证结果的统一性，我们对结果进行归一化。具体方法见下图所示。

接下来我们用matlab进行编程：

首先是main函数：

%topsis
clear;clc
load date;%载入数据
%正向化处理
[n,m] = size(data);
data_x = data_handing(data,n,m);
 disp('正向化矩阵')
disp(data_x)
%标准化处理
data_stm = repmat((sum(data_x.^2, 1)).^(1/2),n-1,1 )
disp('标准化矩阵');
data_standard = data_x./data_stm
%计算得分
Z_max = max(data_standard)
Z_max = repmat(Z_max, n-1, 1)
Z_min = min(data_standard)
Z_min =  repmat(Z_min, n-1, 1)
D_a = sum([(data_standard - Z_max).^2],2).^ 0.5
D_s = sum([(data_standard - Z_min).^2],2).^ 0.5
S_u = D_s./(D_a+D_s)
S_sum = sum(S_u)
S = S_u./S_sum
%排名
[SA,index] = sort(S,'descend')

 其次是数据处理函数data_handing()：

%数据极大化处理函数
function[data_s] = data_handing(data,n, m)%data为原始数据矩阵
data_s = zeros(n-1,m);
for i = 1:m
    test = data(:,i)%提取相对应的列
    if test(1)==1%标准型
        data_s(:,i) = test(2:end,:)
    elseif test(1)==2%中间型
        best  = input('请输入一个bestvalue:')
        M2 = max(abs(test(2:end,:) - best))
        for j = 2:n
            test(j) = 1-abs(test(j)-best)/M2
        end
        data_s(:,i) = test(2:end,:)
    elseif test(1)==3%极小型
        M3 = max(test(2:end,:))
        for k = 2:n
            test(k)=M3 - test(k)
        end
        data_s(:,i) = test(2:end,:)
    elseif test(1)==4%区间型
        low = input('请输入下界:')
        high = input('请输入上界:')
        test = test(2:end,:)
        M_4 = max(test)
        N_4  =min(test)
        M4 = max([low - N_4,M_4 - high])
        for l = 1:(n-1)
            if test(l)high
                test(l) = 1 - (test(l) - high)/M4
            else
                test(l) = 1
            end
        end
            data_s(:,i) = test(1:end,:)
    else
        disp('ERROR!')
    end
end
end

注意1：当程序检测到中间型和区间型指标的时候，我们需要分别在命令窗口键入中间型指标的bestvalue和区间型指标的上下界。

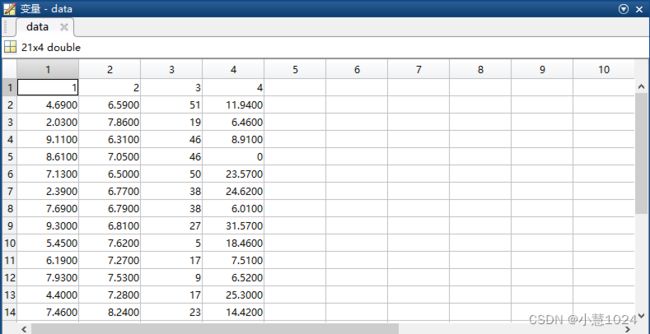
注意2：这两段代码分别为两个文件，分别为topsis.m和data_handing.m文件，需要放在同一个文件夹，而load data需要提前在工作区创建一个叫data的变量，里面存放我们需要处理的topsis数据，见下图所示。

 

注意3：由于我们处理数据的时候需要认为分辨指标的类型，我们对原始数据进行预处理。我们在原始数据的第一行加上指标类型标签，1代表极大型指标，2代表······，小括号的内容不需要键入。

具体步骤见下表所示。

列1	指标1	指标2	指标3	指标4
指标类型	1（极大型）	2（极小型）	3（中间型）	4（区间型）
样本1	4.69	6.59	51	11.94
样本2	2.03	7.86	19	6.46
样本3	9.11	6.31	46	8.91
样本4	8.61	7.05	46	0
样本5	7.13	6.5	50	23.57
样本6	2.39	6.77	38	24.62

 注意4:matlab版本2016a