PyMC3 - GLM之分层线性回归

# 背景 在测量中经常会出现多组相关的结果，比如在计算心理学中对同一个任务中的多个对象进行测试的结果，然后需要估计一组参数来建立一个数学模型，用来描述这个测试任务中的行为。可以对每个测试对象进行独立建模（假设其间不具有共性），也可以将所有的测试对象的结果混在一起统一建模。分层建模兼具这两种方式的优点，可以对测试对象的共性进行建模也可以对每个对象独立的参数进行估计。本文中使用经典的层次线性回归的例子来预测房屋内的氡气水平。 # 数据集 Gelmam等人（2007）的氡气数据集是层次建模的经典数据集。在这个数据集中，测量了在几个州的不同县的不同家庭中的放射性气体氡的数量。通常被认为，存在地下室的家庭中氡气含量更高，并且和土壤类型也有关系。在这里，我们将调查这种差异，并尝试根据县城土壤类型和地下室的存在与否，对不同县的房屋内氡气水平进行预测。

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pymc3 as pm 
import pandas as pd
import theano

data = pd.read_csv('../data/radon.csv')
data['log_radon'] = data['log_radon'].astype(theano.config.floatX)
county_names = data.county.unique()
county_idx = data.county_code.values

n_counties = len(data.county.unique())
print(n_counties)

# 模型需要使用的数据的一小部分
data[['county', 'log_radon', 'floor']].head()

85

	county	log_radon	floor
0	AITKIN	0.832909	1.0
1	AITKIN	0.832909	0.0
2	AITKIN	1.098612	0.0
3	AITKIN	0.095310	0.0
4	ANOKA	1.163151	0.0

数据中，这里是测量的氡气水平（取了对数）；一行代表一栋房屋；有地下室floor==0，没有地下室floor==1。

模型

合并测量

集合所有的测量值来做一个大的回归预测，来判定地下室对氡气水平的影响。数学语言描述如下：

radoni,c=α+β∗floori,c+ϵ

添加的下标 c 表示不同的国家，每个国家进行一次预测，对应一组参数和预测值。c 一共代表 n 个国家，一共会预测出n 个不同的 α 和 β 参数，每组参数对应一个国家。

往往每个国家采集到的数据数量有限，这种方式会带来很大的噪声。

合并部分测量：分层回归

合并测量的方案中，我们假设每个国家有不同的 α 和 β 参数，但是参数的分布系数应该是相同的，可以假设这些参数 αc 和 βc 来自同一个分布。

αc∼(μα,σ2α)

βc∼(μβ,σ2β)

这里假设了 αc 和 βc 来自同一个分布，但是其具体值（后验）需要进行估计，这种方法成为多层模型。

概率编程

非分层模型

首先拟合一个非分层的模型（第一种合并测量），由于对先验没有明确的信息，这里使用零均值、大方差的正态分布作为先验。假设量测值是正态分布，并带有均匀分布的误差 ϵ 。

with pm.Model() as unpooled_model:

    # 每个国家的独立参数
    alpha = pm.Normal('alpha', 0, sd=100, shape=n_counties)
    beta = pm.Normal('beta', 0, sd=100, shape=n_counties)

    # 模型误差
    eps = pm.HalfCauchy('eps', 5)

    # radon含量的数学模型
    radon_est = alpha[county_idx] + beta[county_idx]*data.floor.values

    # Data likelihood
    # 均值就是待预测的radon含量
    # 方差就是测量误差eps
    # 并给定观测值（测量值）
    y = pm.Normal('y', mu=radon_est, sd=eps, observed=data.log_radon)

with unpooled_model:
    unpooled_trace = pm.sample(5000)

Auto-assigning NUTS sampler...
Initializing NUTS using advi...
Average ELBO = -1,745.4: 100%|██████████| 200000/200000 [00:30<00:00, 6452.45it/s]
Finished [100%]: Average ELBO = -1,745.4
100%|██████████| 5000/5000 [00:20<00:00, 244.18it/s]

从结果可以看出，对每个国家的水平的均值（alpah）做出了预测，但是地下室的影响由于混杂咋在一起，噪声太大，预测值均为0附近。

pm.traceplot(unpooled_trace);

分层模型

不同于为每个国家创建一个独立的模型进行估计，分层模型考虑到国家之间不是完全不相同的，有一些内含的相似性，首先估计一组参数，随后用这组参数估计每个国家的参数 α 和 β 的分布，从而估计其后验值。

with pm.Model() as hierarchical_model:

    # 超参数
    # HalfCauchy 柯西半连续型
    # Normal 正态型
    mu_alpha = pm.Normal('mu_alpha', mu=0., sd=100**2)
    sigma_alpha = pm.HalfCauchy('sigma_alpha', 5)
    mu_beta = pm.Normal('mu_beta', mu=0., sd=100**2)
    sigma_beta = pm.HalfCauchy('sigma_beta', 5)

    # 每个国家的参数均服从同一个正态分布
    alpha = pm.Normal('alpha', mu=mu_alpha, sd=sigma_alpha, shape=n_counties)
    beta = pm.Normal('beta', mu=mu_beta, sd=sigma_beta, shape=n_counties)

    # 模型误差
    eps = pm.HalfCauchy('eps', 5)

    # radon含量的模型
    radon_est = alpha[county_idx] + beta[county_idx] * data.floor.values

    # Data likelihood
    # 均值就是待预测的radon含量
    # 方差就是测量误差eps
    # 并给定观测值（测量值）
    radon_like = pm.Normal('radon_like', mu=radon_est, sd=eps, observed=data.log_radon)

with hierarchical_model:
    hierarchical_trace = pm.sample(5000)

Auto-assigning NUTS sampler...
Initializing NUTS using advi...
Average ELBO = -1,090.5: 100%|██████████| 200000/200000 [00:48<00:00, 4139.85it/s]
Finished [100%]: Average ELBO = -1,090.5
100%|██████████| 5000/5000 [00:46<00:00, 107.63it/s]

更具氡气水平的数学模型

radoni,c=αc+βc∗floori,c+ϵc

左半图的边际后验分布可以看出，mu_alpha给出了群组的氡气水平，mu_beta给出了没有地下室对普遍导致了氡气水平的降低（没有大于0的值，因为没有地下室 {floor=1}，而 β 值均为负数，因此没有地下室导致了氡气水平的下降）。

从alpha曲线可以看出对于不同国家的氡气水平是不同的，每条不同颜色的曲线代表一个国家的alpha参数，不同的分布曲线宽度代表了对预测的不同的信心。

pm.traceplot(hierarchical_trace);

后验估计检查

均方根偏差（RMSD）

可以用均方根偏差（Root Mean Square Deviaton, RMSD）来评价哪个模型对数据的描述更为合理。后验估计检查利用估计出的参数重新生成模型数据，并与原始数据进行比较，生成数据更加接近原始数据的模型就是更优的模型，即RMSD越小模型越好。

经过计算，得到两个模型不同的RMSD值（原文代码未给出）：
* individual/non-hierarchical model: 0.13
* hierarchical model: 0.08
可以看出分层模型预测更加准确。

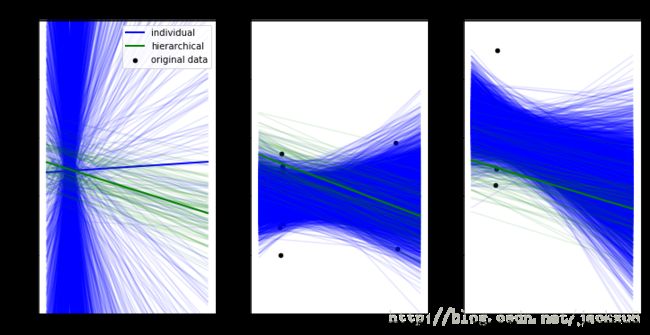
下图以三个国家为例，画出两种模型的预测值和真实值之间的差异。

selection = ['CASS', 'CROW WING', 'FREEBORN']
fig, axis = plt.subplots(1, 3, figsize=(12, 6), sharey=True, sharex=True);
axis = axis.ravel();
for i, c in enumerate(selection):
    c_data = data.ix[data.county == c]
    c_data = c_data.reset_index(drop = True)
    c_index = np.where(county_names==c)[0][0]
    z = list(c_data['county_code'])[0]

    xvals = np.linspace(-0.2, 1.2)
    for a_val, b_val in zip(unpooled_trace['alpha'][1000:, c_index], unpooled_trace['beta'][1000:, c_index]):
        axis[i].plot(xvals, a_val + b_val * xvals, 'b', alpha=.1)
    axis[i].plot(xvals, unpooled_trace['alpha'][1000:, c_index].mean() + unpooled_trace['beta'][1000:, c_index].mean() * xvals, 
                 'b', alpha=1, lw=2., label='individual')
    for a_val, b_val in zip(hierarchical_trace['alpha'][1000:][z], hierarchical_trace['beta'][1000:][z]):
        axis[i].plot(xvals, a_val + b_val * xvals, 'g', alpha=.1)
    axis[i].plot(xvals, hierarchical_trace['alpha'][1000:][z].mean() + hierarchical_trace['beta'][1000:][z].mean() * xvals, 
                 'g', alpha=1, lw=2., label='hierarchical')
    axis[i].scatter(c_data.floor + np.random.randn(len(c_data))*0.01, c_data.log_radon, 
                    alpha=1, color='k', marker='.', s=80, label='original data')
    axis[i].set_xticks([0,1])
    axis[i].set_xticklabels(['basement', 'no basement'])
    axis[i].set_ylim(-1, 4)
    axis[i].set_title(c)
    if not i%3:
        axis[i].legend()
        axis[i].set_ylabel('log radon level')

从上图可以看出，这三个国家中，粗线位两种模型的估计值的均值，蓝色是独立估计的，绿先位分层估计的；细线是后验估计的每个采样的。

对CASS国际的估计，独立估计（蓝线）偏差非常大，因为这个国家的所有房子都有地下室，因此预测出的对于没有地下是对氡气水平的影响是消极的。

而在另外两个国家（右两图），非分层模型对异常值的处理更加的稳健，假设有地下室将带来更高的氡气水平，CROW WING国家的非分层模型预测似乎没有意义。

与频率学派的联系

分层模型在频率学派中有对应的频率效应模型Random effects model，如果将均匀分布作为群组的先验均值，和方差，那么贝叶斯模型和群组效应模型是相同的。