KITTI数据集3d目标检测的评价的含义
kitti数据集评价的含义
- kitti数据集的相关介绍
- kitti数据集3d目标检测的评价
- KITTI 3D AP Metric 的更新
- 参考文献
kitti数据集的相关介绍
- 论文: are we ready for autonomous driving the kitti vision benchmark suite
- kitti数据集下载及解析,参考博客: KITTI数据集下载及解析 和 KITTI数据集下载(百度云) (这两个博客真的良心,感谢作者!!!)
kitti数据集3d目标检测的评价
kitti数据集可以针对很多下游任务。本文只针对3d目标检测的评价数值进行解释。
例子: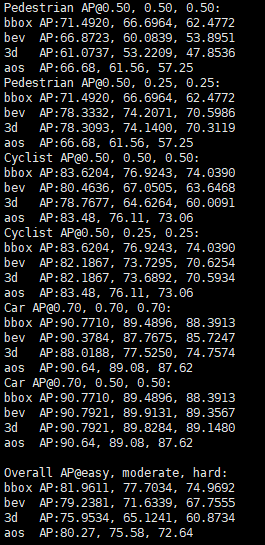
上图是基于mmdetection3d其中一个模型跑出来的kitti验证结果,训练的是3个类别,分别是行人、骑行者和汽车。对于这三个类其实含义一样,以下就以car的数值为例进行解释。
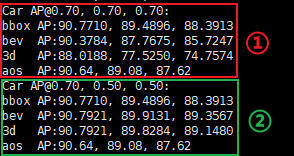
可以看到,对于car的评价结果分成两部分,其实就是两个table。首先解释第一个table:
第一行 Car [email protected], 0.70, 0.70,
Car就是类别(有点废话),AP=average precision(平均准确率),后面三个0.70都是指IOU threshold(目标检测中用于评价预测输出包围框与真实框的重叠情况,设置阈值,从而判断预测结果是否为positive)。需要注意第一个0.70是bbox对应的IOU,第二个0.70是bev对应的IOU,第三个0.70是3d对应的IOU。(2022.06.15修改,之前没有描述清楚,带来误导,不好意思)
第二、三、四行的bbox、bev和3d是对应的三种评价情况。bbox就是2d下的检测。bev=bird-view detection,即鸟瞰图下的检测。3d就是指3d下的检测。(这三种情况应该很好理解)
所以,第一行的三个0.70分别就是对应这三种情况的IOU threshold,例如在bev下,只有当预测输出与真实框的IOU大于0.70,才认为该输出是正确的。
对于二、三、四、五行,每一行都有三个数值,分别对应的是easy、moderate和hard下的评估结果。对于数据集是如何划分难度的,可以参考原论文are we ready for autonomous driving the kitti vision benchmark suite。顾名思义,难度越来越大,所以数值也越来越小,很合理。
第五行的aos=average orientation similarity,平均朝向相似度,用于评价预测输出的朝向与真实框的朝向的相似程度,通俗来说就是朝向预测得是否准确,当然越高越好。
第一个表格讲完,到第二个表格。其实第二个表格的解释和第一个表格一模一样,唯一区别就是三个IOU改为了0.70,0.50,0.50。
即对于bbox,IOU阈值没有改变,那既然IOU没有改变,那么结果当然是一模一样的,所以可以看到两个表格的第二行的数值是完全一样的。
对于第三和第四行,IOU阈值降低了(从0.70, 0.70降低到了0.50, 0.50),通俗含义就是要求降低了,所以评估的AP结果当然提高了,所以第二个表格在第三和第四行的结果比第一个表格要高。
最后一行,AOS,对于该指标,它的计算条件在一二个表格里都是相同的。
KITTI 3D AP Metric 的更新
在论文:Disentangling Monocular 3D Object Detection 中对KITTI 3D的评价指标进行了回顾,以及提出了修改:由原来的AP(实际为 A P ∣ R 11 ) AP|_{R_{11}}) AP∣R11)修改为了 A P ∣ R 40 AP|_{R_{40}} AP∣R40。而且KITTI官方也认可了该指标。详情请看下图以及官网信息。
![]()
(基本就是翻译和理解上述论文的部分,更多细节可以看上述论文)
下面先简单回顾 A P ∣ R 11 AP|_{R_{11}} AP∣R11,该标准的全称或许可以(因为我也不太清楚全称应该是什么,所以这里写或许,见谅)称为 11-point Interpolated Average Precision,表示11点插值平均精度,其公式为
A P ∣ R = 1 ∣ R ∣ ∑ r ∈ R ρ i n t e r p ( r ) AP|_{R}=\frac{1}{|R|}\sum_{r\in R}\rho_{interp}(r) AP∣R=∣R∣1∑r∈Rρinterp(r), 插值函数 ρ i n t e r p ( r ) = max r ′ : r ′ ≥ r ρ ( r ′ ) \rho_{interp}(r)=\max_{r':r'\geq r}\rho(r') ρinterp(r)=maxr′:r′≥rρ(r′),
在KITTI 3D中 R 11 = { 0 , 0.1 , 0.2 , ⋯ , 1 } R_{11}=\{0, 0.1, 0.2, \cdots, 1\} R11={0,0.1,0.2,⋯,1},是等间距的recall level。
但是,从插值函数的形式,它并不是取每个 r r r 时实际的观察值的平均值,而是取其中的最大值。 r r r 从0开始取,则如果只有单个预测,且是正确匹配的,则此时对应的 ρ i n t e r p ( 0 ) = 1 \rho_{interp}(0)=1 ρinterp(0)=1 。如果每个 r r r 都能够提供单一的且正确匹配的预测,那么整个数据集的 A P ∣ R 11 = 1 11 ≈ 0.0909 AP|_{R_{11}}=\frac{1}{11}\approx0.0909 AP∣R11=111≈0.0909,在论文Disentangling Monocular 3D Object Detection 中的实验结果(见论文的Table 4)中,这个精度已经超过了很多方法,显然这无法正确地评估算法的质量。
因此,该论文中提出:不对41个点进行下采样,直接利用40个点进行AP的计算,即将 R 11 R_{11} R11 简单修改为 R 40 = { 1 40 , 2 40 , 3 40 , ⋯ , 1 } R_{40}=\{\frac{1}{40},\frac{2}{40},\frac{3}{40}, \cdots, 1\} R40={401,402,403,⋯,1}。基本都是采用后者进行AP的计算了。
参考文献
- What is the resuls meaning?
