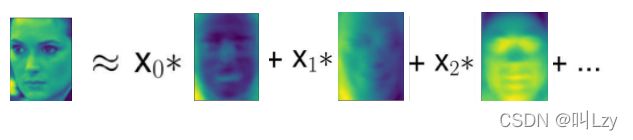主成分分析与其在人脸识别中的应用

最近在自学图灵教材《Python机器学习基础教程》，在csdn以博客的形式做些笔记。

我们在利用无监督学习进行数据变换可能有很多种目的。最常见的目的就是可视化、压缩数据，以及寻找信息量更大的数据表示以用于进一步的处理。而主成分分析是最简单也是最常用的一种方法。

主成分分析

主成分分析（principal component analysis，PCA）是一种旋转数据集的方法，旋转后的特征在统计上不相关。在做完这种旋转之后，通常是根据新特征对解释数据的重要性来选择它的一个子集。

下面将举例说明主成分分析在二维数据集上的应用。

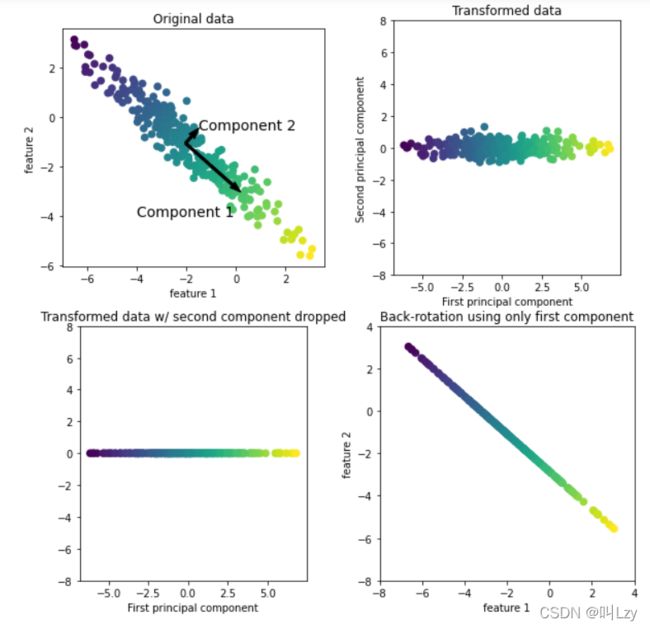
如上图所示，左上角为原始数据。主成分分析算法首先会找到数据集中方差最大的方向，将该方向记为“成分1”（Component 1）。很容易理解，该方向就是包含最多信息的方向，也就是说沿着这个方向的特征之间最为相关。然后算法将会找到与第一个方向正交且包含最多信息的方向（在上图的二维例子中只有一个正交方向，但是在多维空间中具有无数个正交方向）。利用上述过程找到的方向被称之为主成分（principal component），也就是数据方差的主要方向。主成分的个数一般与数据的特征个数相同。

对于第二幅图（右上角），我们对原始数据进行旋转，使得第一主成分与x轴平行，且第二主成分与y轴平行。当然，在旋转之前，我们对原始数据进行了减去平均值的操作，使得变换后的数据以0为中心。在 PCA 找到的旋转表示中，两个坐标轴是不相关的，也就是说，对于这种数据表示， 除了对角线，相关矩阵全部为零。

对于第三幅图（左下角），我们通过保留第一主成分对数据使用PCA进行降维。这将数据从二维数据集降为一维数据集。但要注意，我们没有保留原始特征之一，而是找到了包含信息最多的方向（第一张图中从左上到右下）并保留这一方向，即第一主成分。

最后，我们可以反向旋转并将平均值重新加到数据中。这样会得到右下角最后一张图中的数据。这些数据点位于原始特征空间中，但我们仅保留了第一主成分中包含的信息。这种变换有时用于去除数据中的噪声影响，或者将主成分中保留的那部分信息可视化。

高维数据集可视化

PCA最常见的应用之一就是可以将高维数据进行可视化。对于我们熟知的Iris（鸢尾花）数据集（特征量少），我们可以创建散点图矩阵，通过展示特征所有可能的两两组合来展示数据的局部图像。但如果我们想要查看乳腺癌数据集（特征量多），即便用散点图矩阵也很困难。这个数据集包含30个特征，这就导致需要绘制 30 * 14 = 420 张散点图，我们永远不可能仔细观察所有这些图像，更不用说试图理解它们了。但是，我们还可以用另一种可视化方法：对每个特征分别计算两个类别（良性肿瘤和恶性肿瘤）的直方图。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
cancer= load_breast_cancer()
fig, axes = plt.subplots(15, 2, figsize=(10, 20))
malignant = cancer.data[cancer.target == 0]
benign = cancer.data[cancer.target == 1]
ax = axes.ravel()
for i in range(30):
 _, bins = np.histogram(cancer.data[:, i], bins=50)
 ax[i].hist(malignant[:, i], bins=bins, color=mglearn.cm3(0), alpha=.5)
 ax[i].hist(benign[:, i], bins=bins, color=mglearn.cm3(2), alpha=.5)
 ax[i].set_title(cancer.feature_names[i])
 ax[i].set_yticks(())
ax[0].set_xlabel("Feature magnitude")
ax[0].set_ylabel("Frequency")
ax[0].legend(["malignant", "benign"], loc="best")
fig.tight_layout()

 我们为每一个特征都创建了一个直方图，计算具有某一特征的数据点在特定范围内的出现频率。每张图都包含两个直方图，一个是良性类别的所有点（蓝色），一个是 恶性类别的所有点（绿色）。这样我们可以了解每个特征在两个类别中的分布情况，也可以猜测哪些特征能够更好地区分良性样本和恶性样本。例如，“smoothness error”特征似乎 没有什么信息量，因为两个直方图大部分都重叠在一起，而“worst concave points”特征 看起来信息量相当大，因为两个直方图的交集很小。

但是这种图无法展现出变量之间的相互作用。而利用PCA我们可以获取主要的相互作用。下面将利用前两个主成分，并在这个新的二维空间中利用散点图将数据进行可视化。

from sklearn.decomposition import PCA
from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
cancer = load_breast_cancer()
#在应用 PCA 之前，我们利用 StandardScaler 缩放数据，使每个特征的方差均为 1
scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)
# 保留数据的前两个主成分
pca = PCA(n_components=2)
# 对乳腺癌数据拟合PCA模型
pca.fit(X_scaled)
# 将数据变换到前两个主成分的方向上
X_pca = pca.transform(X_scaled)
# 对第一个和第二个主成分作图，按类别着色
plt.figure(figsize=(8, 8))
mglearn.discrete_scatter(X_pca[:, 0], X_pca[:, 1], cancer.target)
plt.legend(cancer.target_names, loc="best")
plt.gca().set_aspect("equal")
plt.xlabel("First principal component")
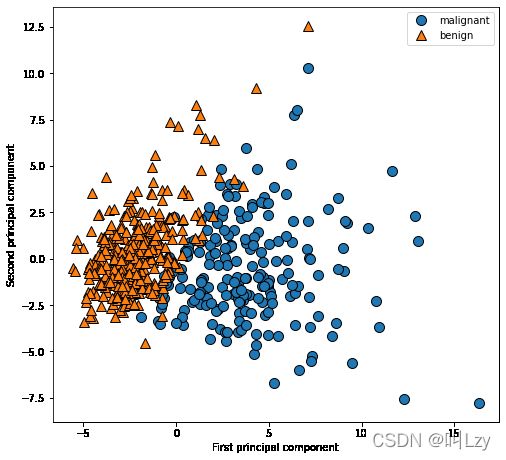
plt.ylabel("Second principal component")

PCA 是一种无监督方法，在寻找旋转方向时没有用到任何类别信息。它只是观察数据中的相关性。对于这里所示的散点图，我们绘制了第一主成分与第二主成分的关系，然后利用类别信息对数据点进行着色。可以看到，在这个二维空间中两个类别被很好地分离。所以说，即使是线性分类器（在这个空间中学习一条直线）也可以 在区分这个两个类别时表现得相当不错。我们还可以看到，恶性点比良性点更加分散，这 一点也可以在上文的直方图中看出来。

人脸识别——特征提取的特征脸

 PCA 的另一个应用是特征提取。特征提取背后的思想是，可以找到一种数据表示，比给定的原始表示更适合于分析。特征提取很有用，它的一个很好的应用实例就是图像。

下面我们将运用PCA处理 Wild 数据集 Labeled Faces （标记人脸）中的人脸图像。这一数据集包含从互联网下载的名人脸部图像，它包含从 21 世纪初开始的政治家、歌手、演员和运动员的人脸图像。

from sklearn.datasets import fetch_lfw_people
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
fix, axes = plt.subplots(2, 5, figsize=(15, 8),
 subplot_kw={'xticks': (), 'yticks': ()})
for target, image, ax in zip(people.target, people.images, axes.ravel()):
 ax.imshow(image)
 ax.set_title(people.target_names[target])

 上图为Wild数据集中Labeled Faces的一些图像展示；该数据集一共有 3023 张图像，每张大小为 87 像素 ×65 像素，分别属于 62 个不同的人。我们下面来看看这个数据集中每一个目标出现的次数。

# 计算每个目标出现的次数
counts = np.bincount(people.target)
# 将次数与目标名称一起打印出来
for i, (count, name) in enumerate(zip(counts, people.target_names)):
 print("{0:25} {1:3}".format(name, count), end=' ')
 if (i + 1) % 3 == 0:
    print()

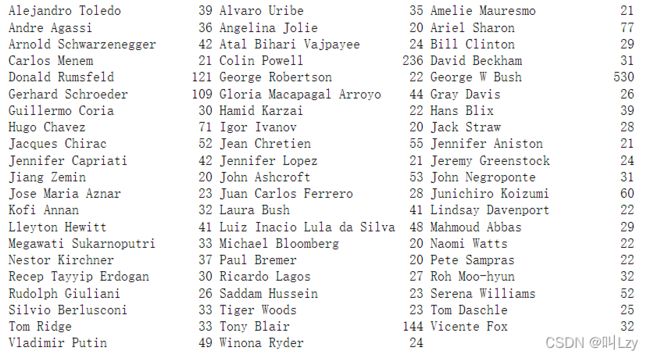
我们可以发现 其中包含 George W. Bush和 Colin Powell的大量图像，因此该数据集具有一定的偏斜。为了降低数据偏斜，我们对每个人最多只取 50 张图像（否则，特征提取将会被 George W. Bush 的可能性大大影响）

mask = np.zeros(people.target.shape, dtype=np.bool)
for target in np.unique(people.target):
 mask[np.where(people.target == target)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
# 将灰度值缩放到0到1之间，而不是在0到255之间
# 以得到更好的数据稳定性
X_people = X_people / 255

我们接下来构建一个简单的KNN分类器（K=1），寻找与你要分类的人脸最为相似的人脸。

from sklearn.neighbors import KNeighborsClassifier
# 将数据分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
 X_people, y_people, stratify=y_people, random_state=0)
# 使用一个邻居构建KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print("Test set score of 1-nn: {:.2f}".format(knn.score(X_test, y_test)))

我们得到的精度为0.23。也就是说每识别四次会成功一次。这对于有62个类别的分类问题来说，其实并不算差（随机猜测的精度为1/62），但是确实也并不太好。于是我们可以用PCA ,想要度量人脸的相似度，计算原始像素空间中的距离是一种不好的方法。用像素表示来比较两张图像时，我们比较的是每个像素的灰度值与另一张图像对应位置的像素灰度值。这种表示与人们对人脸图像的解释方式有很大不同，使用这种原 始表示很难获取到面部特征。例如，如果使用像素距离，那么将人脸向右移动一个像素将·会发生巨大的变化，得到一个完全不同的表示。我们希望，使用沿着主

#我们对训练数据拟合 PCA 对象，并提取前 100 个主成分。然后对训练数据和测试数据进行
#变换
pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
#新数据有 100 个特征，即前 100 个主成分。现在，可以对新表示使用单一最近邻分类器来
#将我们的图像分类
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train_pca, y_train)
print("Test set accuracy: {:.2f}".format(knn.score(X_test_pca, y_test)))

 我们的精度有了相当显著的提高，从 23% 提升到 31%，这证实了我们的直觉，即主成分可能提供了一种更好的数据表示。

接下来我们将看看前几个主成分

fix, axes = plt.subplots(3, 5, figsize=(15, 12),
 subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(pca.components_, axes.ravel())):
 ax.imshow(component.reshape(image_shape),
 cmap='viridis')
 ax.set_title("{}. component".format((i + 1)))

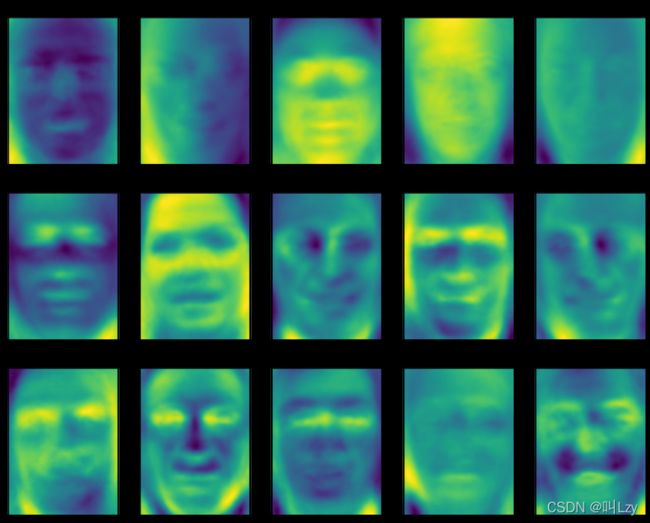
 虽然我们肯定无法理解这些成分的所有内容，但可以猜测一些主成分捕捉到了人脸图像的哪些方面。第一个主成分似乎主要编码的是人脸与背景的对比，第二个主成分编码的是人 脸左半部分和右半部分的明暗程度差异，如此等等。虽然这种表示比原始像素值的语义稍 强，但它仍与人们感知人脸的方式相去甚远。由于 PCA 模型是基于像素的，因此人脸的 相对位置（眼睛、下巴和鼻子的位置）和明暗程度都对两张图像在像素表示中的相似程度 有很大影响。但人脸的相对位置和明暗程度可能并不是人们首先感知的内容。在要求人们 评价人脸的相似度时，他们更可能会使用年龄、性别、面部表情和发型等属性，而这些属 性很难从像素强度中推断出来。重要的是，算法对数据（特别是视觉数据，比如人们非常熟悉的图像）的解释通常与人类的解释方式大不相同。

我们对 PCA 变换的介绍是：先旋转数据，然后删除方 差较小的成分。另一种有用的解释是尝试找到一些数字（PCA 旋转后的新特征值），使我们可以将测试点表示为主成分的加权求和。

 

 这里 x0、x1 等是这个数据点的主成分的系数，换句话说，它们是图像在旋转后的空间中的 表示。

我们还可以用另一种方法来理解 PCA 模型，就是仅使用一些成分对原始数据进行重建。 在图 3-3 中，在去掉第二个成分并来到第三张图之后，我们反向旋转并重新加上平均值， 这样就在原始空间中获得去掉第二个成分的新数据点，正如最后一张图所示。我们可以对 人脸做类似的变换，将数据降维到只包含一些主成分，然后反向旋转回到原始空间。回到 原始特征空间可以通过 inverse_transform 方法来实现。这里我们分别利用 10 个、50 个、 100 个和 500 个成分对一些人脸进行重建并将其可视化。

 可以看到，在仅使用前 10 个主成分时，仅捕捉到了图片的基本特点，比如人脸方向和明暗程度。随着使用的主成分越来越多，图像中也保留了越来越多的细节。这对应于上文的求和中包含越来越多的项。如果使用的成分个数与像素个数相等，意味着我们在旋转后 不会丢弃任何信息，可以完美重建图像。