从零开始的数模（八）TOPSIS模型

一、概念

1.1评价方法概述

1.2概念 

TOPSIS （Technique for Order Preference by Similarity to an Ideal Solution ）模型中文叫做“逼近理想解排序方法”，是根据评价对象与理想化目标的接近程度进行排序的方法，是一种距离综合评价方法。基本思路是通过假定正、负理想解，测算各样本与正、负理想解的距离，得到其与理想方案的相对贴近度（即距离正理想解越近同时距离负理想解越远），进行各评价对象的优劣排序

1.3相关概念 

1.4相关步骤 

1.4.1对原始决策矩阵正向化

1.4.2计算加权后的矩阵

 1.4.3确定正理想解C和负理想解C0 

 有点乱例题为先！！！ 

二、python实现

import numpy as np  # 导入numpy包并将其命名为np
 
##定义正向化的函数
def positivization(x,type,i):
# x：需要正向化处理的指标对应的原始向量
# typ：指标类型（1：极小型，2：中间型，3：区间型）
# i：正在处理的是原始矩阵的哪一列
    if type == 1:  #极小型
        print("第",i,"列是极小型，正向化中...")
        posit_x = x.max(0)-x
        print("第",i,"列极小型处理完成")
        print("--------------------------分隔--------------------------")
        return posit_x
    elif type == 2:  #中间型
        print("第",i,"列是中间型")
        best = int(input("请输入最佳值："))
        m = (abs(x-best)).max()
        posit_x = 1-abs(x-best)/m
        print("第",i,"列中间型处理完成")
        print("--------------------------分隔--------------------------")
        return posit_x
    elif type == 3:  #区间型
        print("第",i,"列是区间型")
        a,b = [int(l) for l in input("按顺序输入最佳区间的左右界，并用逗号隔开：").split(",")]
        m = (np.append(a-x.min(),x.max()-b)).max()
        x_row = x.shape[0]  #获取x的行数
        posit_x = np.zeros((x_row,1),dtype=float)
        for r in range(x_row):
            if x[r] < a:
               posit_x[r] = 1-(a-x[r])/m
            elif x[r] > b:
               posit_x[r] = 1-(x[r]-b)/m
            else:
               posit_x[r] = 1
        print("第",i,"列区间型处理完成")
        print("--------------------------分隔--------------------------")
        return posit_x.reshape(x_row)
 
 
## 第一步：从外部导入数据
#注：保证表格不包含除数字以外的内容
x_mat = np.loadtxt('river.csv', encoding='UTF-8-sig', delimiter=',')  # 推荐使用csv格式文件
 
## 第二步：判断是否需要正向化
n, m = x_mat.shape
print("共有", n, "个评价对象", m, "个评价指标")
judge = int(input("指标是否需要正向化处理，需要请输入1，不需要则输入0："))
if judge == 1:
    position = np.array([int(i) for i in input("请输入需要正向化处理的指标所在的列，例如第1、3、4列需要处理，则输入1,3,4").split(',')])
    position = position-1
    typ = np.array([int(j) for j in input("请按照顺序输入这些列的指标类型（1：极小型，2：中间型，3：区间型）格式同上").split(',')])
    for k in range(position.shape[0]):
        x_mat[:, position[k]] = positivization(x_mat[:, position[k]], typ[k], position[k])
    print("正向化后的矩阵：", x_mat)
 
## 第三步：对正向化后的矩阵进行标准化
tep_x1 = (x_mat * x_mat).sum(axis=0)  # 每个元素平方后按列相加
tep_x2 = np.tile(tep_x1, (n, 1))  # 将矩阵tep_x1平铺n行
Z = x_mat / ((tep_x2) ** 0.5)  # Z为标准化矩阵
print("标准化后的矩阵为：", Z)
 
## 第四步：计算与最大值和最小值的距离，并算出得分
tep_max = Z.max(0)  # 得到Z中每列的最大值
tep_min = Z.min(0)  # 每列的最小值
tep_a = Z - np.tile(tep_max, (n, 1))  # 将tep_max向下平铺n行,并与Z中的每个对应元素做差
tep_i = Z - np.tile(tep_min, (n, 1))  # 将tep_max向下平铺n行，并与Z中的每个对应元素做差
D_P = ((tep_a ** 2).sum(axis=1)) ** 0.5  # D+与最大值的距离向量
D_N = ((tep_i ** 2).sum(axis=1)) ** 0.5
S = D_N / (D_P + D_N)  # 未归一化的得分
std_S = S / S.sum(axis=0)
sorted_S = np.sort(std_S, axis=0)
print(std_S)  # 打印标准化后的得分
## std_S.to_csv(std_S.csv)  结果输出到std_S.csv文件

import pandas as pd
import numpy as np

#读取数据
data=pd.read_excel('投标单位各项指标和分值.xlsx')

#数据标准化
label_need=data.keys()[1:]
data1=data[label_need].values
[m,n]=data1.shape
data2=data1.copy().astype('float')
for j in range(0,n):
    data2[:,j]=data1[:,j]/np.sqrt(sum(np.square(data1[:,j])))

#计算加权重后的数据
w=[0.3724, 0.1003,0.1991, 0.1991,0.0998,0.0485]   #使用求权重的方法求得,参见文献1
R=data2*w

#计算最大最小值距离
r_max=np.max(R,axis=0)   #每个指标的最大值
r_min=np.min(R,axis=0)   #每个指标的最小值
d_z = np.sqrt(np.sum(np.square((R -np.tile(r_max,(m,1)))),axis=1))  #d+向量
d_f = np.sqrt(np.sum(np.square((R -np.tile(r_min,(m,1)))),axis=1))  #d-向量  

#计算得分
s=d_f/(d_z+d_f )
Score=100*s/max(s)
for i in range(0,len(Score)):
    print(f"第{i+1}个投标者百分制得分为：{Score[i]}") 

案例：

 
 
import numpy as np
import pandas as pd
 
#TOPSIS方法函数
def Topsis(A1):
    W0=[0.2,0.3,0.4,0.1] #权重矩阵
    W=np.ones([A1.shape[1],A1.shape[1]],float)
    for i in range(len(W)):
        for j in range(len(W)):
            if i==j:
                W[i,j]=W0[j]
            else:
                W[i,j]=0
    Z=np.ones([A1.shape[0],A1.shape[1]],float)
    Z=np.dot(A1,W) #加权矩阵
    
    #计算正、负理想解
    Zmax=np.ones([1,A1.shape[1]],float)
    Zmin=np.ones([1,A1.shape[1]],float)
    for j in range(A1.shape[1]):
        if j==3:
            Zmax[0,j]=min(Z[:,j])
            Zmin[0,j]=max(Z[:,j])
        else:
            Zmax[0,j]=max(Z[:,j])
            Zmin[0,j]=min(Z[:,j])
 
    #计算各个方案的相对贴近度C
    C=[]  
    for i in range(A1.shape[0]):
            Smax=np.sqrt(np.sum(np.square(Z[i,:]-Zmax[0,:])))
            Smin=np.sqrt(np.sum(np.square(Z[i,:]-Zmin[0,:])))
            C.append(Smin/(Smax+Smin))
    C=pd.DataFrame(C,index=['院校' + i for i in list('12345')])   
    return C
 
#标准化处理
def standard(A):
    #效益型指标
    A1=np.ones([A.shape[0],A.shape[1]],float)
    for i in range(A.shape[1]):
        if i==0 or i==2:
            if max(A[:,i])==min(A[:,i]):
                A1[:,i]=1
            else:
                for j in range(A.shape[0]):
                    A1[j,i]=(A[j,i]-min(A[:,i]))/(max(A[:,i])-min(A[:,i]))
    
    #成本型指标
        elif i==3:
            if max(A[:,i])==min(A[:,i]):
                A1[:,i]=1
            else:
                for j in range(A.shape[0]):
                    A1[j,i]=(max(A[:,i])-A[j,i])/(max(A[:,i])-min(A[:,i])) 
 
    #区间型指标
        else:
            a,b,lb,ub=5,6,2,12
            for j in range(A.shape[0]):
                if lb <= A[j,i] < a:
                    A1[j,i]=(A[j,i]-lb)/(a-lb)
                elif a <= A[j,i] < b:
                    A1[j,i]=1		
                elif b <= A[j,i] <= ub:
                    A1[j,i]=(ub-A[j,i])/(ub-b)
                else:  #A[i,:]< lb or A[i,:]>ub
                    A1[j,i]=0	
    return A1
 
#读取初始矩阵并计算
def data(file_path):
    data=pd.read_excel(file_path).values
    A=data[:,1:]
    A=np.array(A)
    #m,n=A.shape[0],A.shape[1] #m表示行数,n表示列数
    return A
 
#权重
A=data('研究生院评估数据.xlsx')
A1=standard(A)
C=Topsis(A1)
print(C)

 三、MATLAB实现

3.1数据处理

function [posit_x] = Min2Max(x)
    posit_x = max(x) - x;
     %posit_x = 1 ./ x;    %如果x全部都大于0，也可以这样正向化
end

 

function [posit_x] = Mid2Max(x,best)
    M = max(abs(x-best));
    posit_x = 1 - abs(x-best) / M;
end

function [posit_x] = Inter2Max(x,a,b)
    r_x = size(x,1);  % row of x 
    M = max([a-min(x),max(x)-b]);
    posit_x = zeros(r_x,1);   %zeros函数用法: zeros(3)  zeros(3,1)  ones(3)
    % 初始化posit_x全为0  初始化的目的是节省处理时间
    for i = 1: r_x
        if x(i) < a
           posit_x(i) = 1-(a-x(i))/M;
        elseif x(i) > b
           posit_x(i) = 1-(x(i)-b)/M;
        else
           posit_x(i) = 1;
        end
    end
end

 3.2例题

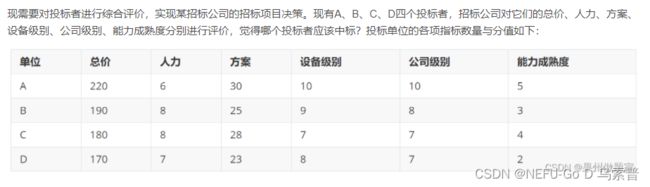
成绩是越高（大）越好，这样的指标称为极大型指标（效益型指标）。
与他人争吵的次数越少（越小）越好，这样的指标称为极小型指标（成本型指标）。

在进行分析的时候我们需要将指标统一为一个类型，一般都转为极大型指标。

3.2.1 指标正向化

将所有的指标转化为极大型称为指标正向化（最常用）

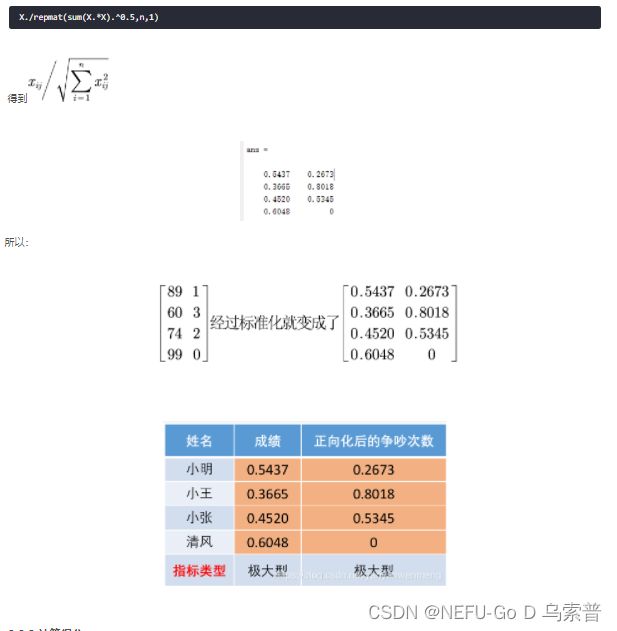
3.2.2 指标标准化处理 

只有一个指标的时候不需要消除量纲的影响，但是2个指标及以上呢？

由于成绩和争吵次数的量纲不同（单位不同），所以需要消除指标对不同量纲的影响。

为了消去不同指标量纲的影响，需要对已经正向化的矩阵进行标准化处理

 可以发现标准化后不会影响到指标的相对大小。

matlab代码：B = repmat(A,m,n):将矩阵A复制m×n块，即把A作为B的元素，B由m×n个A平铺而成。

X = [89 1; 60 3; 74 2; 99 0]
[n,m] = size(X)
X./repmat(sum(X.*X).^0.5,n,1)

 

 

3.2.4 实例计算 

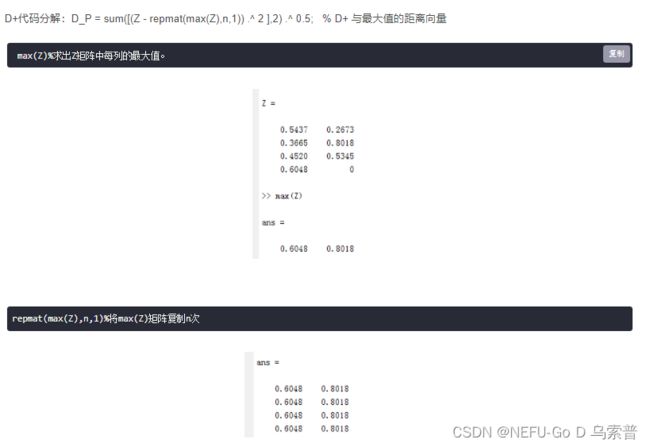
X = [89,1; 60,3; 74,2;99,0]%已经正向化后的矩阵
[n,m] = size(X)
Z = X./repmat(sum(X.*X) .^ 0.5,n,1)%标准化
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N);    % 未归一化的得分