机器学习--贝叶斯网

1-概念

贝叶斯网（Bayesian network）亦称信念网，它借助有向无环图DAG,来刻画属性自己建得依赖关系，并使用条件概率表来描述属性得联合概率分布。是一种经典的概率图模型。

贝叶斯网络（BN）是一种概率图形模型，用于在医学，生物学，流行病学，经济和社会科学等各个领域的不确定性下进行推理。

具体来说，BN用于回答诸如“这种干预的可能效果是什么？”或“哪些因素与这种影响相关？”之类的问题
一个贝叶斯网B由结构有向无环图(DAG)G和参数θ两部分构成。B=

• 网络结构G是一个有向无环图，每个节点对应一个属性，若两个属性有直接依赖关系，则它们由一条边连接起来 G=(X,E)
• 参数θ定量描述这种依赖关系

2-DAG示例

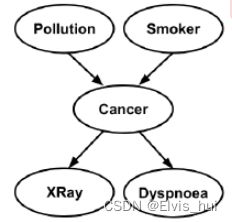
在癌症DAG中，“污染”和“吸烟者”是“癌症”的父母，他们也被称为“癌症”的直接原因。这种有向边缘编码依赖性和独立性的关系，例如，“污染”和“吸烟者”是独立的，“吸烟者”和“癌症”是依赖的。

参数集 θ 表示基于这些依赖性和独立性的条件概率，例如：
$$P(XRay\mid Cancer,Smoker)=P(XRay\mid Cancer)$$
概率分布可以是离散的，也可以是连续的。如果分布是离散的，则通常表示为表格概率。

推断DAG,G和参数集θ，是BN两个主要问题。参数集是在知道DAG后确定的，因此我们专注与Bayesian network structure learning

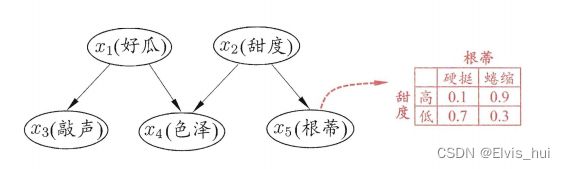
西瓜书种给出一个例子，西瓜问题的一种贝叶斯网结构和属性"根蒂"的条件概率表 从图中网络结构可看出 色泽" 直接依赖于 "好瓜 “和"甜度”，而"根蒂"则直接依赖于"甜度"进一步从条件概率表能得到"根蒂"对"甜度"量化依赖关系?如 P( 根蒂=硬挺 |甜度=高）= 0.1等。

3-BN结构

学习BN的结构是一个NP-hard问题,Robinson（1973）表明递归关系：
$$|G_n|=\sum _{i=1}^n(-1{)}^{i-1}{(}_i^n)2^{i(n-i)}|G_{n-i}|$$
它是 n 个变量的可能 DAG 数。如果我们有8个变量，则可能的DAG数将为7.8e11，随着变量数的增加，DAG的数量呈超指数级增长
$$\begin{gathered} 贝叶斯网结构有效地表达了属性间的条件独立性。给定父结点集，贝叶斯网假设每个属性与它的非后裔属性独立，于是 \\ B=<G,\theta >将属性X1,x2,...,Xd联合概率分布定义为 \\ {P}_B(x_1,x_2,...,x_d)=\prod _{i=1}^d{P}_B(x_i|{\pi }_i)=\prod _{i=1}^d{\theta }_{x_i{\pi }_i} \\ 以上图为例，联合概率分布定义为 \\ P(x_1,x_2,x_3,x_4,x_5)=P(x_1)P(x_2)P(x_3|x_1)P(x_4|x_1,x_2)P(x_5|x_2) \\ 显然x_3,x_4在给定的取值时独立,x_4和x_5在给定x_2的取值时独立，分别简记x_3\perp x_4|x_1和x_4\perp x_5|x_2 \end{gathered}$$

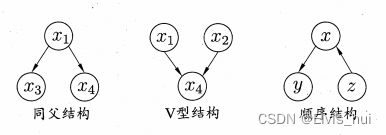
4-BN中3个变量之间的依赖关系

$$\begin{gathered} 同父结构：给定父结点町的取值，则x_3,x_4条件独立. \\ 顺序结构：给定x的值，则y和z条件独立 \\ V型结构：亦称为冲撞结构，给定子节点x_4的取值，x_1和x_2必不独立。 \\ 奇妙的是，若x_4的取值完全未知，则V型结构下x_l,x_2却是相互独立的: \\ P(x_1,x_2)=\sum _{x_4}P(x_1,x_2,x_4)=\sum _{x_4}P(x_4|x_1,x_2)P(x_1)P(x_2)=P(x_1)P(x_2) \\ 这种独立成为边际独立x_1⫫x_2 \end{gathered}$$
由于BN的网络结构是不知道的，因此BN learning 的首要任务是根据训练数据集找出结构最”恰“的BN，评分搜索是求解这一问题的常用办法。

评分搜索，我们先定义一个评分函数(score function) ，以此来评估BN与训练数据的契合程度，然后基于这个评分函数来寻找结构最优的贝叶斯网.
$$\begin{gathered} 给定训练集D=\{x_1,x_2,...,x_m\},贝叶斯网B=<G,\theta >在D上的评分函数可写为： \\ s(B|D)=f(\theta )|B|-LL(B|D) \end{gathered}$$

$$\begin{gathered} |B|是BN的参数个数； \\ f(\theta )表示描述每个参数\theta 所需的字节数 \\ LL(B|D)=\sum _{i=1}^{m}log{P}_B(x_i)贝叶斯网B的对数似然。 \end{gathered}$$

目标：寻找一个贝叶斯网B使得评分函数s( B| D)最小
$$\begin{gathered} f(\theta )=1，表示每个参数用1个字节描述，得到AIC评分函数AkaikeInformationCriterion \\ AIC评分函数：AIC(B|D)=|B|-LL(B|D) \\ f(\theta )=\frac{logm}{2}，表示每个参数用\frac{logm}{2}个字节描述，得到BIC评分函数BayesianInformationCriterion \\ BIC评分函数：BIC(B|D)=\frac{logm}{2}|B|一LL(B|D) \\ f(\theta )=0,，则评分函数退化为负对数似然，相应的，学习任务退化为极大似然估计. \end{gathered}$$
推导结果
$$\begin{gathered} 若贝叶斯网B=<G，\theta >的网络结构固定,则评分函数s(B|D)的第一项为常数.此时，最小化s(B|D)等价于对参 \\ 数\theta 的极大似然估计,LL(B|D)=\sum _{i=1}^{m}log{P}_B(x_i)和P_B(x_1,x_2,...,x_d)=\prod _{i=1}^d{P}_B(x_i|{\pi }_i)=\prod _{i=1}^d{\theta }_{x_i{\pi }_i}可知 \\ ,参数{\theta }_{x_i|{\pi }_i}能直接在训练数据D上通过经验估计获得:{\theta }_{x_i|{\pi }_i}={\hat{P}}_D(x_i|{\pi }_i),其中\hat{P}(\cdot )是D上的经验分布， \\ 为了最小化评分函数只需对网络结构进行搜索，而候选结构的最优参数可直接在训练集上计算得到. \end{gathered}$$

5-吉布斯采样算法

推断-这样通过已知变量观测值来推测待查询变量的过程
证据-己知变量观测值

在现实应用中，BN的近似推断常使用吉布斯采样(Gibbs sampling)来完成

$$P(Q=q|E=e)\simeq \frac{n_q}{T}$$
吉布斯采样算法

需注意的是，由于马尔可夫链通常需很长时间才能趋于平稳分布，因此吉布斯采样算法的收敛速度较慢.
此外，若贝叶斯网中存在极端概率 “0"或"1” ，则不能保证马尔可夫链存在平稳分布，此时吉布斯采样会给出错误的估计结果。

基于约束的方法，基于一系列条件独立性测试（CI tests）消除和定向边缘。基于分数的方法代表了一种传统的机器学习方法，其目的是搜索不同的图形，从而最大化目标函数。结合基于分数和基于约束的方法的混合算法。

6-代码部分

#可视化安装graphviz
pip install graphviz
#光pip是不够的，需要去官网下载graphviz，配置环境变量
#安装贝叶斯网
pip install pgmpy

pgmpy 参数说明

## 读取数据
Taidf = pd.read_csv("data/chap9/tatdf.csv")#来自泰坦尼克号的数据
Taidf = Taidf.drop("IsAlone",axis = 1) ## 删除一个不重要的变量
## 将年龄变量Age和Fare变量转化为分类变量
X = Taidf[["Age","Fare"]].values
Kbins  = KBinsDiscretizer(n_bins=[3,3],    #每个变量分别分为3份 
                          encode="ordinal",#分箱后的特征编码为整数
                          strategy = "kmeans")##每个变量执行k均值聚类过程的分箱策略
X_Kbins = Kbins.fit_transform(X)
X = Taidf[["Age","Fare"]] = np.int8(X_Kbins)
print(Taidf.head())

>>
>   Survived  Pclass  Name  Sex  Age  SibSp  Parch  Fare  Embarked
0         0       3     2    1    0      1      0     0         2
1         1       1     3    0    1      1      0     0         0
2         1       3     1    0    1      0      0     0         2
3         1       1     3    0    1      1      0     0         2
4         0       3     2    1    1      0      0     0         2

## 随机选择75%的数据作为训练集,也可直接用
#from sklearn.model_selection import train_test_split
#train_df,test_df=train_test_split(data,train_size=0.75)

trainnum = round(Taidf.shape[0] * 0.75)
np.random.seed(123)
index = np.random.permutation(Taidf.shape[0])[0:trainnum]
traindf = Taidf.iloc[index,:]
testdf = Taidf.drop(index,axis=0)
test_Survived = testdf["Survived"]
print("训练样本:",traindf.shape)
print("测试样本:",testdf.shape)
>>
>训练样本: (668, 9)
 测试样本: (223, 9)

0-自定义贝叶斯网络

import os
os.environ["PATH"] += os.pathsep + 'C:/Program Files/Graphviz/bin'#自己安装可视化工具的目录

## 根据前面的决策树模型，自定义一个简单的贝叶斯网络
model = BayesianModel([("Fare","Survived"), ("Pclass","Survived"),
                       ("SibSp","Survived"),("Pclass","Fare"),
                       ("Name", "Pclass"),("Name","SibSp"),
                       ("Sex", "Pclass"),("Sex","Name")])
## 调用graphviz绘制贝叶斯网络的结构图
node_attr = dict(shape="ellipse",color = "lightblue2", style = "filled")
dot = Digraph(node_attr=node_attr)  # 定义一个图
dot.attr(rankdir="LR")   # 指定图的可视化放心为左右
edges = model.edges()    # 获取网络的边
for a,b in edges:
    dot.edge(a,b)
    
>>dot
>

>>model.nodes()
>NodeView(('Fare', 'Survived', 'Pclass', 'SibSp', 'Name', 'Sex'))

## 模型使用的变量
usevarb = list(model.nodes())
model_traindf = train_df[usevarb]
model_testdf = test_df[usevarb]
model_testdf = model_testdf.drop(["Survived"],axis = 1)
## 根据数据拟合模型
model.fit(data = model_traindf,estimator=BayesianEstimator)

## 使用模型对测试集进行预测
model_pre = model.predict(model_testdf)
model_acc = accuracy_score(test_Survived.values,model_pre)
print("贝叶斯网络在测试集上的精度为:",model_acc)
## 可以发现自定义的网络在测试集上的预测精度为0.6367

1-搜索所有网络结构

## 使用训练数据学习一个贝叶斯网络
## 如果变量较少可以使用ExhaustiveSearch搜索所有的贝叶斯网络
## 一般要求变量数小于5

## 根据数据中的3个变量利用ExhaustiveSearch进行网络搜索
model_estraindf = traindf[["Name","Sex","Pclass","Survived"]]
model_estestdf = testdf[["Name","Sex","Pclass"]]
bic = BicScore(model_estraindf)
# bic.score(BayesianModel([("Sex","Survived")]))
model_es = ExhaustiveSearch(model_estraindf, scoring_method=bic)
best_model = model_es.estimate()
# print("较好网络的边为:\n",best_model.edges())
## 调用graphviz绘制贝叶斯网络的结构图
node_attr = dict(shape="ellipse",color = "lightblue2", style = "filled")
dot = Digraph(node_attr=node_attr)  # 定义一个图
dot.attr(rankdir="LR")   # 指定图的可视化放心为左右
edges = best_model.edges()    # 获取网络的边
for a,b in edges:
    dot.edge(a,b)
>>dot

## 输出不同的网络对应的bic值,评分越高，网络越合理
bicscore = []
nbgraph = []
for score, dag in reversed(model_es.all_scores()):
    bicscore.append(score)
    nbgraph.append(dag.edges())
## 组成数据表格
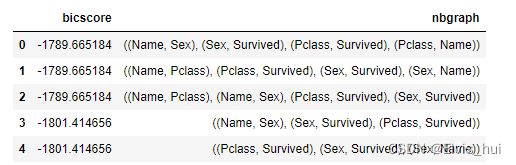
model_esdf = pd.DataFrame(data= {"bicscore":bicscore,"nbgraph":nbgraph})
model_esdf.head()
## 可以发现前三个网络的评分是一样的

绘制前三个网络

## 可视化前三个网络
## 调用graphviz绘制贝叶斯网络的结构图
node_attr = dict(shape="ellipse",color = "lightblue2", style = "filled")
## 可视化第一个网络
dot = Digraph(node_attr=node_attr)  
dot.attr(rankdir="LR")   
edges = nbgraph[0]   
for a,b in edges:
    dot.edge(a,b)
## 可视化第二个网络
dot1 = Digraph(node_attr=node_attr) 
dot1.attr(rankdir="LR")  
edges1 = nbgraph[1]   
for a,b in edges1:
    dot1.edge(a,b)
## 可视化第三个网络
dot2 = Digraph(node_attr=node_attr)  
dot2.attr(rankdir="LR")  
edges2 = nbgraph[2]    
for a,b in edges2:
    dot2.edge(a,b)   

1
2
3

## 使用最好的网络建立模型并预测测试集的精度
best_model = BayesianModel(best_model.edges())
best_model.fit(data = model_estraindf,estimator=BayesianEstimator)
model_pre = best_model.predict(model_estestdf)
model_acc = accuracy_score(test_Survived.values,model_pre)
print("贝叶斯网络在测试集上的精度为:",model_acc)
>>
>贝叶斯网络在测试集上的精度为: 0.7533632286995515

2-启发式搜索网络结构

train_df,test_df=train_test_split(data,train_size=0.75)

## 启发式搜索网络结构
bic = BicScore(train_df)
# bic.score(BayesianModel([("Sex","Survived")]))
# hc = HillClimbSearch(train_df, scoring_method=bic)
hc = HillClimbSearch(train_df)
best_model = hc.estimate()
# print("启发式搜索到的网络结构为:\n",best_model.edges())
## 调用graphviz绘制贝叶斯网络的结构图
node_attr = dict(shape="ellipse",color = "lightblue2", style = "filled")
dot = Digraph(node_attr=node_attr)  # 定义一个图
dot.attr(rankdir="LR")   # 指定图的可视化放心为左右
edges = best_model.edges()    # 获取网络的边
for a,b in edges:
    dot.edge(a,b)
>>
>dot

## 使用最好的网络建立模型并预测测试集的精度
best_model = BayesianModel(best_model.edges())
best_model.fit(data = train_df,estimator=BayesianEstimator)
model_pre = best_model.predict(test_df.drop("Survived",axis = 1))
## 可以发现虽然获得的网路更加的复杂了，但是网络的预测精度并没有显著的提升
model_acc = accuracy_score(test_df["Survived"].values,model_pre)
print("贝叶斯网络在测试集上的精度为:",model_acc)
>>
>贝叶斯网络在测试集上的精度为: 0.7892376681614349