PyTorch nn.Linear学习记录
记录一下 PyTorch nn.Linear 的学习过程。
概述
首先,从 PyTorch 的官方文档,可以发现 nn.Linear 是一个类(面向对象语言)。它的作用是对输入数据 x (列向量)做线性变换(Ax)和偏置(+b)后得到输出数据 y(列向量)。即
y = A x + b y=Ax+b y=Ax+b
其中 A 是线性变换矩阵,A有 m 行,n 列。x、y、b分别代表一条输入数据、一条输出数据、一条输出数据对应的偏置,分别是 n 行、m 行、m行的列向量。有读者可能注意到 PyTorch 官方文档给出的式子是 y = x A T + b y=xA^T+b y=xAT+b,但是本文不采用这个写法。理由是本文认为这个写法和上面的写法表达了一样的内涵,可以认为这个写法是上面写法方程两边同时取了转置,这个写法中向量为行向量。
下文先介绍 nn.Linear 的基本信息,并且对其机理做详细介绍,最后举了一个简单的线性回归例子。
一、
代码 1展示创建一个 nn.Linear 类的对象。输出 1 打印了关于该对象的信息。输出 1 告诉我们该对象的输入向量有 2 个分量,输出向量有 3 个分量。还打印了 nn.Linear 类对象的 参数矩阵(随机生成的)和偏置向量。细心的读者可能发现了参数矩阵有 3 行、2 列。为什么不是 2 行、3 列呢?(可能产生该疑惑的理由是代码第3行:torch.nn.Linear(2,3)建立了一个输入特征为 2 个分量的向量,输出特征为 3 个分量的向量的 nn.Linear 对象)下面通过图1、介绍 参数矩阵的一些特点以及输出是如何得到的
import torch
model = torch.nn.Linear(2, 3);
print('Network Structure : torch.nn.Linear(2,3) :\n', model)
print('Weight Of Network :\n', model.weight)
print('Bias Of Network :\n', model.bias)
输出:
Network Structure : torch.nn.Linear(2,3) :
Linear(in_features=2, out_features=3, bias=True)
Weight Of Network :
Parameter containing:
tensor([[-0.2424, 0.5018],
[ 0.4110, 0.6242],
[ 0.5015, -0.5561]], requires_grad=True)
Bias Of Network :
Parameter containing:
tensor([-0.3397, 0.5143, -0.1039], requires_grad=True)
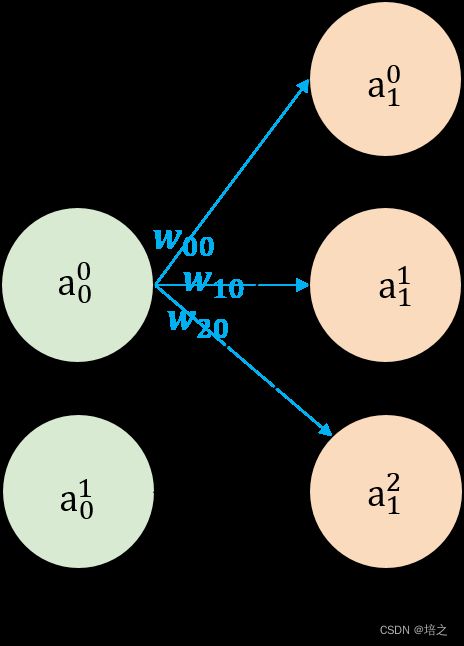
在 nn.Linear 中,是如何得到输出的呢?本文发现用最简单的前向神经网络(只有输入层、输出层而没有隐藏层)来解释比较直观。下图 1 的网络结构和代码 1 中的 nn.Linear(2,3) 生成的 Linear(in_features=2, out_features=3, bias=True) 结构是保持一致的。偏置理解起来比较简单,下文中先不考虑偏置。
首先,图1中每个绿色的神经元代表了输入向量的每个分量;每个粉色神经元代表了输出向量的每个分量。输入层的神经元与输出层的神经元之间有单向箭头直线连接,由输入层的神经元指向输出层的神经元。比如,在 神经元 a 0 0 a_0^0 a00 与 a 1 0 a_1^0 a10 之间有一条直线,而且由前者指向后者,这意味着得到 a 1 0 a_1^0 a10 需要 a 0 0 a_0^0 a00 的信息。但是指向 a 1 0 a_1^0 a10 的神经元不止一个,还有 a 0 1 a_0^1 a01,这意味着只要知道 a 0 0 a_0^0 a00和 a 0 1 a_0^1 a01的值和相关参数,就能计算出 a 1 0 a_1^0 a10的值,具体地:
a 1 0 = a 0 0 w 0 0 + a 0 1 w 0 1 a_1^0 = a_0^0w_0^0+a_0^1w_0^1 a10=a00w00+a01w01
类似地,
a 1 1 = a 0 0 w 1 0 + a 0 1 w 1 1 a_1^1 = a_0^0w_1^0+a_0^1w_1^1 a11=a00w10+a01w11
a 1 2 = a 0 0 w 2 0 + a 0 1 w 2 1 a_1^2 = a_0^0w_2^0+a_0^1w_2^1 a12=a00w20+a01w21
将上述三个等式整理成矩阵乘法的形式,有
[ a 1 0 a 1 1 a 1 2 ] = [ w 00 w 01 w 10 w 11 w 20 w 21 ] [ a 0 0 a 0 1 ] \begin{bmatrix} a_1^0 \\ a_1^1 \\ a_1^2 \end{bmatrix}=\begin{bmatrix} w_{00} & w_{01} \\ w_{10} & w_{11} \\ w_{20}& w_{21} \end{bmatrix}\begin{bmatrix} a_0^0 \\ a_0^1 \end{bmatrix} ⎣⎡a10a11a12⎦⎤=⎣⎡w00w10w20w01w11w21⎦⎤[a00a01]
其中,记输入向量 x x x
x = [ a 0 0 a 0 1 ] x=\begin{bmatrix} a_0^0 \\ a_0^1 \end{bmatrix} x=[a00a01]
参数矩阵 A A A
A = [ w 00 w 01 w 10 w 11 w 20 w 21 ] A=\begin{bmatrix} w_{00} & w_{01} \\ w_{10} & w_{11} \\ w_{20}& w_{21} \end{bmatrix} A=⎣⎡w00w10w20w01w11w21⎦⎤
输出向量 y y y
y = [ a 1 0 a 1 1 a 1 2 ] y=\begin{bmatrix} a_1^0 \\ a_1^1 \\ a_1^2 \end{bmatrix} y=⎣⎡a10a11a12⎦⎤
行文至此,神经网络的图示和参数矩阵 A A A都已经引出来了。不难发现 A A A 的行数和列数分别是 3、2。但是 in_features=2, out_features=3。这是一个规律,即 参数矩阵 A A A 的行数等于 out_features,列数等于 in_features。
所谓的偏置,就是加入一个常数,类似于初高中时候 y = kx+b 中的 b。引入偏置后,
[ a 1 0 a 1 1 a 1 2 ] = [ w 00 w 01 w 10 w 11 w 20 w 21 ] [ a 0 0 a 0 1 ] + [ b 0 b 1 b 2 ] \begin{bmatrix} a_1^0 \\ a_1^1 \\ a_1^2 \end{bmatrix}=\begin{bmatrix} w_{00} & w_{01} \\ w_{10} & w_{11} \\ w_{20}& w_{21} \end{bmatrix}\begin{bmatrix} a_0^0 \\ a_0^1 \end{bmatrix}+\begin{bmatrix} b_0 \\ b_1 \\ b_2 \end{bmatrix} ⎣⎡a10a11a12⎦⎤=⎣⎡w00w10w20w01w11w21⎦⎤[a00a01]+⎣⎡b0b1b2⎦⎤
其中,偏置向量为 b = [ b 0 b 1 b 2 ] b=\begin{bmatrix} b_0 \\ b_1 \\ b_2 \end{bmatrix} b=⎣⎡b0b1b2⎦⎤
到这里,nn.Linear 如何对输入向量做线性变换和偏置后得到输出向量的机理已经介绍完毕。下面即将介绍使用 nn.Linear 对数据集做线性回归的一个例子,以方便读者理解 nn.Linear。
二、
接下来介绍一个简单的用 nn.Linear 做线性回归的例子。
代码 2 导入库文件,生成训练数据集。其中输入为 x_train ,对应的输出为 y_train。
import numpy as np
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
# 生成训练数据:x = [0,1,2,...,10]
x_values = [i for i in range(11)]
x_train = np.array(x_values, dtype=np.float32)
x_train = x_train.reshape(-1, 1)
# y = 2*x+1
y_values = [2*i + 1 for i in x_values]
y_train = np.array(y_values, dtype=np.float32)
y_train = y_train.reshape(-1, 1)
代码 3 是最重要的部分,定义线性回归类 linearRegression。其继承了 torch.nn.Module。在 代码 3 的第 4 行代码中,初始化了一个 nn.Linear 对象。
class linearRegression(torch.nn.Module):
def __init__(self, inputSize, outputSize):
super(linearRegression, self).__init__()
self.linear = torch.nn.Linear(inputSize, outputSize)
def forward(self, x):
out = self.linear(x)
return out
在代码 4 中,第 6 行代码生成了一个类 linearRegression 的对象,命名为 model。倒数第 2 行代码指定 均方误差作为损失函数。最后一行代码指定优化器为随机梯度下降,并且在优化器中指定需要优化的参数为刚刚生成的类 linearRegression 的对象 model 的参数。model 的初始参数应该是随机初始化的。
inputDim = 1 # 'x'
outputDim = 1 # 'y'
learningRate = 0.01
epochs = 100
model = linearRegression(inputDim, outputDim)
##### For GPU #######
if torch.cuda.is_available():
model.cuda()
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learningRate)
在代码5的第 14 行代码 outputs = model(inputs) 中,它实际上调用了 model 的成员函数 forward。但却不是以 model.forward(inputs) 的调用形式调用的,为什么呢?因为类linearRegression继承了 类nn.Module,在类 nn.Module 的派生类中,都从类 nn.Module 那继承了 _call_ 函数,当它们以 model(inputs) 的形式出现时,_call_ 函数会自动调用 forward 函数。
for epoch in range(epochs):
# 将 x,y转换成torch 的 Variable 数据类型
if torch.cuda.is_available():
inputs = Variable(torch.from_numpy(x_train).cuda())
labels = Variable(torch.from_numpy(y_train).cuda())
else:
inputs = Variable(torch.from_numpy(x_train))
labels = Variable(torch.from_numpy(y_train))
# 清除梯度缓冲区,因为不希望上一个 epoch 的梯度影响这个 epoch
optimizer.zero_grad()
# 对给定的输入,预测输出
outputs = model(inputs)
# 从预测输出中得到损失
loss = criterion(outputs, labels)
print(loss)
# 得到关于模型参数的梯度
loss.backward()
# 更新参数
optimizer.step()
print('epoch {}, loss {}'.format(epoch, loss.item()))
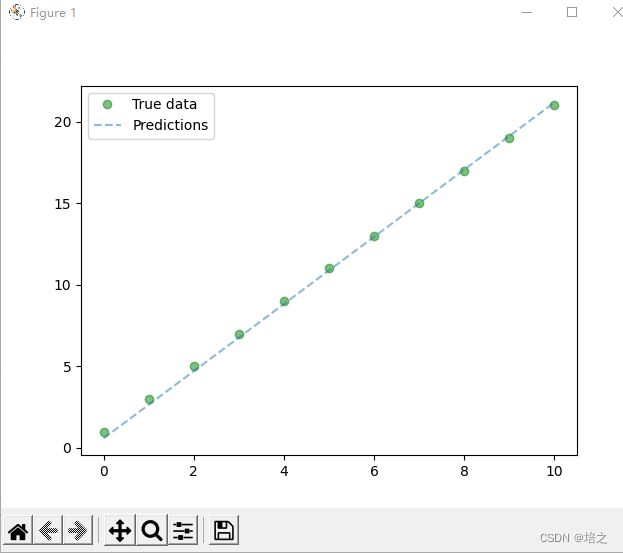
代码 6 的作用是推理和作图。测试集中的离散点在图 2 中是实心点,线性回归得到的线性方程以虚线直线的形式展示。
with torch.no_grad(): # 在测试(推理)阶段不需要计算梯度
if torch.cuda.is_available():
predicted = model(Variable(torch.from_numpy(x_train).cuda())).cpu().data.numpy()
else:
predicted = model(Variable(torch.from_numpy(x_train))).data.numpy()
print(predicted)
plt.clf()
plt.plot(x_train, y_train, 'go', label='True data', alpha=0.5)
plt.plot(x_train, predicted, '--', label='Predictions', alpha=0.5)
plt.legend(loc='best')
plt.show()
三、总结
- 对 nn.Linear 的作用和机理做了解释。
- 用 nn.Linear 类做了简单的线性回归
四、参考
https://pythonguides.com/pytorch-nn-linear/
https://towardsdatascience.com/linear-regression-with-pytorch-eb6dedead817