三维分子图的球面信息传递

参考链接：微信公众号文章

摘要：

我们考虑3D分子图的表示学习，其中每个原子与3D中的空间位置相关。这是一个探索不足的研究领域，目前缺乏一个有原则的消息传递框架。在这项工作中，我们在球坐标系（SCS）中进行分析，以完全识别三维图形结构。基于这些观察，我们提出了球形消息传递（SMP）作为一种新颖而强大的3D分子学习方案。SMP极大地降低了训练的复杂性，使其能够在大规模分子上高效执行。此外，SMP能够区分几乎所有的分子结构，未发现的情况在实践中可能并不存在。基于对三维信息有意义的物理表示，我们进一步提出了用于三维分子学习的SphereNet。实验结果表明，在SphereNet中使用有意义的3D信息可以显著提高预测任务的性能。我们的结果还证明了SphereNet在性能、效率和可扩展性方面的优势

导言：

在许多现实世界的研究中，分子等结构化对象被自然建模为图形。随着深度学习的发展，图形神经网络（GNN）已被开发用于从图形数据中学习。目前，消息传递方案是实现GNN的常用架构之一。在这项工作中，我们的目标是开发一种新的三维图形消息传递方法。通常，3D分子图包含笛卡尔坐标系中给出的每个原子的3D坐标以及图结构。不同类型的相对3D信息可以从3D分子图中获得，它们在分子学习中很重要，例如键长、键间角度。

我们首先研究3D分子的完整表示。这要求图形结构由相关3D信息唯一定义。为此，我们在球坐标系（SCS）中进行了形式化分析，并表明三维图形中每个原子的相对位置由三种几何唯一确定，包括距离、角度和扭转。然而，这种完整性需要涉及基于边缘的两跳信息，导致计算复杂度过高。为了避免计算开销，我们提出了一种新的消息传递方案，称为球形消息传递（SMP），用于快速准确的三维分子学习。我们的SMP在表示3D分子方面是高效且近似完整的。首先，我们设计了一种新的计算扭转的策略，该策略只考虑基于边缘的一跳信息，从而大大降低了训练复杂度。这使得SMP能够推广到大规模分子。此外，我们还表明，我们的SMP可以区分几乎所有的3D图形结构。未发现的案例被清楚地陈述，而且在实践中似乎很少出现。通过自然地使用相对的3D信息和一种新的扭转，SMP产生了对输入图形的平移和旋转不变的预测。

我们将SMP应用于现实世界中的分子学习，其中需要有意义的物理表示。SMP指定的几何体（d，θ，φ）由ψ（d，θ，φ）物理表示，其中可以是薛定谔方程的解，如第4. 基于此，我们开发了球形信息传递神经网络，称为SphereNet，用于3D分子学习. 我们在各种类型的数据集上进行实验，包括OC20、QM9和MD17。结果表明，与基线方法相比，SphereNet在不增加计算预算的情况下实现了最佳性能。消融研究揭示了不同类型3D信息的贡献和必要性，包括距离、角度和扭转。特别是，我们比较了一个完整的消息传递方案，该方案可以区分所有三维图形结构，但涉及基于边缘的两跳信息。实验结果表明，SphereNet的性能相当，但运行时间减少了4倍。这表明在实践中使用SphereNet，而不是完整的消息传递方案，其计算复杂性阻止了它在大分子上的使用

分子的完全表示：

等变图神经网络（EGNN）代表了3D分子图的一个研究领域，如5.1节. 这些方法通常将所有原子的笛卡尔坐标系（CCS）中的坐标作为原始输入。因此，所有网络层都需要仔细设计，使其具有相同的变化。一些等变分量的计算成本很高，比如球谐函数和Clebsh-Gordan系数。此外，复杂的SE群表示对于分子学习可能不是必需的，因为最终表示通常要求是不变的。在这项工作中，我们关注的是另一类方法，它们将相对位置信息纯粹作为图形学习模型的输入。相对的3D信息可以是距离或角度，这对输入分子的平移和旋转具有固有的不变性。在球面坐标系（SCS）中考虑这种信息是很自然的。我们从研究SCS中3D分子的结构识别开始。对于SCS中的任何点，其位置由三元组（d，θ，φ）指定，其中d，θ和φ分别表示径向距离、极角和方位角。在SCS中建模3D分子图时，任何原子i都可以是局部SCS的原点，d、θ和φ自然分别成为键长、键间角度和扭转角。因此，原子i的每个相邻原子的相对位置可以由相应的元组（d，θ，φ）指定。类似地，可以确定每个原子在3D分子图中的相对位置，从而确定结构，该结构对输入图的平移和旋转自然不变。SCS可以很容易地从笛卡尔坐标系转换，因此可以很容易地获得元组（d，θ，φ）

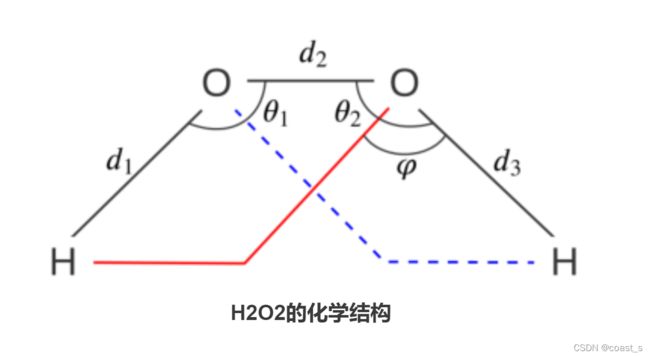
如图1所示，我们使用过氧化氢（H2O2）的化学结构来说明d、θ和φ对分子结构鉴定的重要性。显然，该结构由三个键长d1、d2、d3、两个键角θ1、θ2和扭转角φ唯一定义。请注意，输入可能不包含所有成对距离（所有可能的键长）。这是因为原子连接性通常基于真实的化学键和截止距离。截止距离通常设置为超参数。很难保证截止距离大于分子中的任何成对距离。因此，在本例中，如果截止值很小，H-H键长度可能不会被视为输入。对于其他两个原子之间的距离可能很大的复杂大分子来说，设置一个合适的截止值就更难了。此外，考虑所有成对距离将导致严重的冗余，显著增加计算复杂性。模型也很容易被过多的噪声所迷惑，导致性能不理想。从完备性的角度来看，使用所有成对距离无法识别手性性质。即使考虑了H-H键，也无法区分手性H2O2分子。为了克服上述挑战，我们结合使用距离、角度和扭转进行严格的设计和准确的学习。 显然，两个O-H键可以在不改变任何键长和键角的情况下围绕O-O键旋转。然而，在这种情况下，扭转角φ发生变化，H2O2的结构也随之变化。扭转角的重要性在相关研究领域也得到了证实。Garg等人）正式表明，扭转和端口编号可以提高GNN在区分几何图形属性（如周长和周长）方面的表达能力，其他研究表明，通过考虑给定3D空间中的扭转，可以准确生成蛋白质序列和分子结构。在这项工作中，我们提出SMP系统地考虑距离，角度和扭转的3D分子图的近似完整的表示学习。注意，通过使用角度和扭转，SMP可以很容易地识别手性性质

球形消息传递:

消息传递方案
目前，一类消息传递神经网络（MPNN）是GNN最广泛使用的架构之一。基于Sec中的完整性分析。我们建议在球面坐标系（SCS）中执行消息传递，从而产生了一种新的高效方案，称为球面消息传递（SMP）。我们证明了现有方法（如SchNet和DimeNet）中使用的消息传递方案是SMP的特例
我们首先正式定义了一个三维分子图，它通常表示为一个四元组G=（u，V，E，P）。u是分子图G的全局特征向量。V={vi}i=1:n是原子特征集，其中每个vi原子i的特征向量，即E={（ek，rk，sk）}(k=1:m)是一组边，其中每个ek∈ R是特征向量，rk是接收原子的索引，sk是边k的发送原子的索引。P={rh}(h=1:n)是包含每个原子的三维空间信息的三维笛卡尔坐标集。此外，我们让Ei={（ek，rk，sk）}(rk=i，k=1:m)表示指向原子i的边集，Ni表示原子i的传入节点的索引。消息传递过程后的输出包括更新的全局特征向量u′∈ R，更新的原子特征V′={V′i}i=1:n，更新的边E′={（E′k，rk，sk）}(k=1:m)
图2（a）中提供了用于SMP的消息聚合方案的图示。显然，原子rk的嵌入是通过聚合每个传入消息ek获得的。消息ek基于Esk更新，Esk是指向atom sk的一组传入消息。让q表示Esk中任何消息的发送方原子。因此，我们可以定义一个本地SCS，其中sk作为原点，消息ek的方向自然作为z轴。我们定义sk的相邻原子o为参考原子。因此，参考平面由三个原子sk、rk和o构成。对于原子q，其位置由元组（d、θ、φ）唯一定义，如图4（a）所示。具体地说，d确定它到原子sk的距离，θ指定它更新消息ek的方向。扭转角φ由定义的参考平面和sk、rk和q跨越的平面构成。直观地说，作为3D图形球坐标中的高级消息传递体系结构，SMP通过考虑所有距离、角度和扭转角信息来指定任何相邻原子q的相对位置，从而为3D分子图提供更全面的表示
通常，sk原子可能有几个相邻的原子，我们称之为q1…qt。计算这些t原子相应的键长和键角很容易。SMP通过将所有t原子投影到垂直于ek并与sk相交的平面来计算扭转角。然后在这个平面上，扭转角在预定义的方向上形成，比如逆时针方向。通过这样做，任何原子都会自然地成为逆时针方向下一个原子的参考原子。值得注意的是，这些t扭转角之和为2π。图2（b）中示出了简化的情况。sk原子有三个相邻的原子q1、q2和q3；q3是q1的参考原子，它们形成φ1；q1是q2的参考原子，它们形成φ2；同样地q2是q3的参考原子，它们形成φ3。很明显，φ1、φ2和φ3之和是2π。由于扭距是相对定义的，因此可以任意选取q1，这不会影响消息传递方案的输出，因为我们在将来自其邻居q1、q2和q3的信息聚合到sk时执行求和。值得注意的是，通过将每个原子设计为预定义方向上下一个原子的参考原子，可以有效地实现不变性，因为参考原子自然是相对的。此外，我们的方法在基于边缘的1-hop邻域内计算扭转。即使扭转角包含四个原子，我们的设计避免了扭转角的数量是指数的，但使其与相邻原子的数量相同。因此，它是高效的，不会导致时间或内存问题。在形式上，提议的SMP可在SCS中定义为：

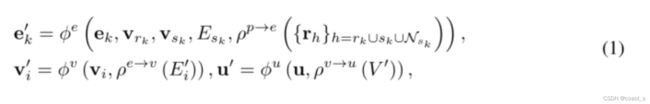
其中φe、φv和φu分别是边、原子和整个图形上的三个信息更新函数。ρe→v和ρv→u在不同类型的几何图形之间聚合信息。尤其是在SMP中，P中的3D信息被转换并合并以更新每个消息。因此，SMP采用了另一个位置聚合函数ρp→e用于消息更新。值得注意的是，我们在公式1中定义的SMP方案与Battaglia等人（2018年）的GN框架之间的主要区别在于包含了3D信息P。与第节所述的研究领域一致。5.1.2.我们专注于此类3D信息，并开发一个系统解决方案，以全面有效地整合这些信息。这些功能的详细说明见附录A
完整性与效率
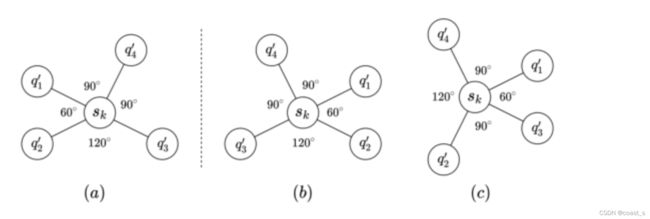
识别标准可以完全确定3D分子的结构，但涉及基于边缘的两跳信息。因此，计算复杂度相当于O（nk3），其中n表示原子数，k表示每个中心原子的相邻原子的平均数。不幸的是，这种设计很难推广到大分子图。为此，我们提出SMP作为一种高效且可扩展的方案来实现SCS中的消息传递。我们的SMP只涉及基于边缘的1跳信息，因此时间复杂度降低到O（nk2）。这使得SMP能够应用于大分子，比如新发布的OC20数据（Chanussot等人，2020年）。我们严格研究了SMP的完整性，并表明它甚至可以区分复杂的几何性质，如手性，如图3（a）和图3（b）所示。由于SMP在预定义方向上使用最后一个原子作为参考原子（如图2（b）中q2是q3的参考原子），因此考虑相邻原子之间的相对顺序，而忽略绝对顺序。因此，SMP无法区分图3（b）和图3（c）所示的两种分子。然而，这种情况在自然界中可能并不存在。实验也证明了这一点，我们的SMP实现了与完整表示相当的性能，而完整表示会导致巨大的时间复杂性和严重的内存问题。

与先前消息传递方法的关系
在开发3D图形的消息传递方法时，球体消息传递是一种高级方案，其中每个原子的相对位置更为明确。三维图形的开发与相关信息仍处于早期阶段。据我们所知，文献中存在几种值得注意的方法，它们可以被视为SMP的特例，因为它们捕获部分3D位置信息。例如，SnNETs和PopyNETs考虑距离，DimeNet编码方向信息。在形式上，这些方法可以完美地拟合公式1中定义的球面格式。我们在附录C中描述了这些方法的细节。值得注意的是，与之前的模型相比，SMP提供了关于其完整性的严格理由，并清楚地描述了故障案例。重要的是，SMP是基于3D分子图的识别分析开发的。因此，它的目标是学习3D分子图的完整数据表示，而不是简单地包含额外的3D信息（如角度或扭转）。

SPHERENET：

得到的三元组（d，θ，φ）表示三维分子图中任何原子的相对位置。然而，它不能作为神经网络的直接输入，因为它缺乏有意义的表示。本质上，分子是量子系统，因此表征设计需要遵循物理定律。一个重要的方面是选择合适的基函数，将三元组（d，θ，φ）转换为基于物理的表示。Hu等人（2021年）探讨了几个基本函数；Klicpera等人（2020b），包括MLP、高斯和正弦函数、球贝塞尔基和球谐函数。特别地，球面贝塞尔被证明是编码距离的最佳基础，球面谐函数是编码角度最合适的一个（胡等人，2021；KLIPRA等人，2020B）。我们将最终表示形式表示为ψ（d，θ，φ）。参考Griffiths&Schroeter（2018）的理论；科恩等人（2019年）；Klicpera等人（2020b），一种表示形式可以表示为…，其中jℓ（·）是一个有序的球形贝塞尔函数ℓ, Y mℓ 是一个阶数为m的球谐函数ℓ, c表示截止值βℓn是贝塞尔阶函数的第n个根ℓ. 我们也有ℓ ∈ [0，··，L− 1] ，m∈ [−ℓ, · · · , ℓ] 和n∈ [1，··，N]。L和N分别表示球谐函数和球贝塞尔函数的最高阶。它们是实验环境中的超参数。此外，我们还可以从ψ（d，θ，φ）导出两种简化表示形式ψ（d）和ψ（d，θ）。基于第节中描述的球形消息传递方案。3和物理表征，我们为分子学习构建SphereNet。显然，SphereNet可以生成既准确又有物理意义的数据表示。通过将位置信息合并到球坐标中，SphereNet还可以生成对输入分子的平移和旋转不变性的预测。遵循第2.2节中所述的研究路线中的架构设计。5.1.2我们的网络由一个输入块、几个交互块和一个输出块组成。为了清楚地描述，我们假设图2中用于边缘k的消息ek和等式（1）是用于更新的消息。SphereNet的更新过程和详细架构见附录B。

相关工作:

三维分子图的绘制方法
等变图神经网络
3D分子图的一个研究方向是等变图神经网络（EGNN），包括张量场网络（TFN）（Thomas等人，2018）、SE（3）-变压器（Fuchs等人，2020）、PaiNN（Schütt等人，2021）、NequIP（Batzner等人，2021）等。这些方法的原始输入通常包含绝对信息，例如笛卡尔坐标系中的坐标。在中间层，可以根据需要将绝对信息分解为部分绝对信息和部分相对信息。一个简单的例子是，向量可以分解为方向（绝对）和长度（相对）（Thomas等人，2018年；Schütt等人，2021年）。显然，这些方法的网络组件应该仔细设计为等变量。TFNs等前期工作是为3D点云开发的。然而，研究表明，对于下游任务通常要求系统保持不变的分子，复杂的SE（3）基团表示是不必要的，但S2表示就足够了（Klicpera et al.，2021）。此外，它们在分子任务上的表现并不令人满意
不变图神经网络
另一类方法纯粹将相对的3D信息作为输入，例如原子之间的距离、键之间的角度、平面之间的角度等。因此，网络是自然不变的。这些方法的开发尚处于早期阶段，现有的研究侧重于利用不同的几何形状。SchNet（Schütt等人，2017年）通过使用连续滤波器卷积层，在信息聚合阶段合并了距离信息。PhysNet（Unke&Meuwly，2019年）将原子特征和距离信息整合到提议的交互块中。DimeNet（Klicpera et al.，2020b）是基于PhysNet开发的，通过考虑交互块中的方向信息向前推进了一步。GemNet（Klicpera等人，2021年）最近被提出用于通用分子表征。OrbNet（乔等人，2020年）将距离信息与原子轨道理论相结合，设计重要的SAAO特征，作为GNNs的输入。通常，使用3D位置信息通常会提高性能。然而，现有的方法仅仅包括额外的几何图形，如距离和角度，并且对于不同的几何图形如何影响信息聚合过程缺乏严格的理由。我们进行了形式化分析，表明所有的距离、角度和扭转都是三维分子识别所必需的，在此基础上，我们提出了SphereNet来生成更强大的分子表示
其他建模为图形的对象的方法
除了分子外，许多其他数据对象也被表示为图形，如3D点云（郭等，2020；Simunokys＆KoODaKIS，2017；Sin等人，2018；Land Riueun和Simunovs’，2018）和网格（BrangSin等人，2021；De Haan等人，2020；Pelruuin等人，2019）。将三维点云建模为三维图形时，点表示为节点，点之间的连接表示为有向边。现有的方法主要是从三维空间的局部邻域获取距离信息。在DGCNN（Wang等人，2019b）中，提出了一种新的层，即EdgeConv，用于聚合基于距离的边缘特征，用于节点学习。在Landrieu&Boussaha（2019）中，邻域半径和空间方向被纳入局部点嵌入。Wang等人（2019a）的工作提出了一种3D点云的图形注意卷积。通常，这些方法可以适用于等式1中定义的消息传递方案。De Haan等人（2020年）的工作是一项示范性研究，该研究将网格表示为图形，并考虑几何信息。所使用的卷积核取决于预定义参考边与投影到每个顶点切面的任何其他边之间的角度。它侧重于规范等变的设计，而不是学习完整的几何信息。在这项工作中，我们研究了3D分子的完整学习，并留下了对其他数据类型的广泛研究作为未来的工作

实验研究 :

实验设置：
我们将SphereNet应用于三个基准数据集，包括Open Catalyst 2020（OC20）（Chanussot等人，2020年）、QM9（Ramakrishnan等人，2014年）和MD17（Chmiela等人，2017年）。基线方法包括PPGN（Maron et al.，2019）、SchNet（Schutt et al.，2017）、PhysNet（Unke&Meuwly，2019）、Cormorant（Anderson et al.，2019）、PaiNN（Schutt et al.，2021）、NequIP（Batzner et al.，2021）、MGCN（Lu et al.，2019）、DimeNet（Klicpera et al.，2020b）、DimeNet++（Klicpera et al.，2020a）、GemNet（Klicpera et al.，2021），CGCNN（Xie&Grossman，2018）和sGDML（Chmiela等人，2018）。补充材料中提供了以下章节中使用的所有型号的详细配置。除非另有规定，对于所有基线方法，我们报告的结果取自参考文献或原始作者提供的结果。对于SphereNet，所有模型都使用Adam优化器进行训练（Kingma&Ba，2014）。通过网格搜索得到最优超参数。附录D中提供了所有型号的网络配置和搜索空间。代码包含在补充材料中

OC20:
表1:SphereNet与IS2RE上其他模型在能量MAE和地面真能量EwT百分比方面的比较。在All训练数据集上训练的模型报告的结果。最佳结果以粗体显示 ：

表2:SphereNet和其他模型在最大可用能量和QM9上总平均标准最大可用能量方面的比较表示参考文献中未报告有关相应性质的结果。最佳结果以粗体显示，次佳结果以下划线显示

化学结构空间使得机器学习模型可以得到充分训练。在这项工作中，我们主要关注IS2RE任务，附录E中提供了数据描述。Chanussot等人（2020年）提供了CGCNN、SchNet和DimeNet++的结果。最初的GemNet论文不包含OC20数据集的结果，我们使用OC项目网站1中的公开代码为GemNet-T生成结果。我们报告SphereNet的固定时代的评估结果。按照Chanusso等人（2020）的设置，我们使用直接方法和所有训练模型的训练数据。使用的指标是能量MAE和地面真能量阈值（EwT）内的能量百分比。
表1显示，SphereNet在4次拆分中有3次达到最佳性能，在能量MAE方面达到平均值。对于EwT，SphereNet在所有4个拆分中都是最好的。具体来说，它将平均能量MAE降低了0.019，这是次优模型的3.10%。此外，它将平均EwT从3.42%提高到3.64%，考虑到EwT固有的低值，这是一个很大的幅度。值得注意的是，ForceNet（Hu等人，2021年）和GemNet（Klicpera等人，2021年）最近被提议用于量子系统学习。ForceNet的一个显著优势是它的高效性和可扩展性。ForceNet专注于S2EF，因此IS2RE任务没有原始结果。然而，DimeNet++在性能方面略优于ForceNet，我们的SphereNet明显优于DimeNet++。GemNet有两个变体GemNet-T和GemNet-Q。GemNet将距离和角度信息作为输入，并包含一个有效的体系结构，具有新颖的网络组件，如双线性层和比例因子。我们可以看到GemNet-T在性能方面与DimeNet++类似。GemNet-Q据称能够捕捉分子的普遍表征。然而，它考虑了基于边缘的两跳信息，时间复杂度极高。它无法正确配置，无法在大催化剂分子上进行实验
表3:SphereNet与其他模型在MD17上的MAE力比较。WoFE表示损耗函数中力与能量的重量。所有基线模型的结果都直接取自或改编自原始论文（如果单位不同），SphereNet根据不同基线的原始论文使用两个WOFE进行公平比较。最佳结果以粗体显示，次佳结果以下划线显示

QM9
我们将SphereNet应用于QM9数据集，该数据集广泛用于预测分子的各种性质。它由多达9个重原子组成的有机分子组成。因此，该测试可以检验SphereNet对于类似量子化学系统的能力。数据集最初分为三组，其中训练集包含110000个，验证集包含10000个，测试集包含10831个分子。对于与能源相关的属性，培训过程使用单位eV。所有超参数都在验证集上进行了调优，并应用于测试集。我们使用每个属性的平均绝对误差（MAE）和所有12个属性的总体平均标准化MAE（标准MAE），将SphereNet与基线进行比较。表2总结了比较结果。SphereNets在5个属性上的性能最好，在3个属性上的性能次之。此外，它还将QM9数据集的整体平均标准偏差从0.98提高到了0.91，并开创了最新水平。值得注意的是，PaiNN最近的方法在样本数方面使用了与SphereNet相同的数据分割。它的最终性能是在三次随机拆分上三次不同运行的平均值。我们遵循这些设置，在四个属性上运行SphereNet，包括ϵHOMO、ϵLUMO、U0和µ。相应的结果分别为22.9±0.2、18.8±0.2、6.28±0.05和0.0243±0.00。很明显，这些结果与表2中的结果非常接近，因此，我们可以得出一致的结论

MD17
MD17数据集用于检查SphereNet在分子动力学模拟中的表达能力。遵循Schütt等人（2017）的设置；Klicpera等人（2020b），我们为每个分子训练了一个单独的模型来预测原子力。我们使用1000个样本进行训练，八个分子中的每一个都有验证集和测试集。请注意，所有基线模型在训练期间都采用了联合损失力和守恒能量的方法。在SchNet（Schütt et al.，2017）和DimeNet（Klicpera et al.，2020b）的原始论文中，作者将力与能量的权重（WoFE）设置为100，而NequIP（Batzner et al.，2021）和GemNet（Klicpera et al.，2021）的论文使用的权重为1000。由于WoFE往往会显著影响力的预测，为了公平比较，我们使用两个WoFE值进行SphereNet。PaiNN（Schütt等人，2021年）既不使用100也不使用1000作为WoFE，因此我们不会在MD17上与它进行比较。力的结果如表3所示。请注意，对于苯，所有模型均以苯17进行评估，因此，sGDML的结果为0.20，而不是0.06（苯18）。我们可以从表中观察到，当所有型号的WoFE为100时，SphereNet的利润率始终高于SchNet和DimeNet。值得注意的是，sGDML是创建具有精心设计的功能的MD17数据集的原创作品之一。与sGDML相比，SphereNet在四种分子上的性能更好，在其他四种分子上的性能更差，这与DimeNet类似。一个原因是sGDML结合了分子对称性以提高精度，不同的分子具有不同的对称性。然而，sGDML对于没有手工设计功能的较大数据集的泛化能力较差。此外，SphereNet还取得了很多成就整体标准MAE优于sGDML。当使用相同的WoFE（即1000）时，SphereNet与GemNet取得了类似的结果，尽管GemNet-T的复杂性很高，并且包含精心设计的网络组件以提高性能。

完整性与效率
GemNet中的消息传递方案Q-MP代表了基于边缘的2跳几何消息传递，可以生成完整的三维分子图表示。我们通过与Q-MP的比较研究了所提出的SMP的性能和效率。具体来说，我们对这两种MP方法使用相同的主干网络，以进行公平比较。我们广泛使用两个主干，这是Klicpera等人（2021年）提出的GemNet主干。我们在MD17上进行实验，使用相同的计算基础设施（Nvidia GeForce RTX 2080 TI 11GB）报告每个历元所有8个分子的性能和平均运行时间。结果如表4所示，从中我们可以观察到，在任一主干网络上，SMP与Q-MP的结果非常相似。然而，时间成本远低于SMP，这表明它比Q-MP更有效。根据Sec的分析。3.2，SMP可以区分几乎所有的分子结构，并且失效案例在自然界中可能不存在。因此，SMP的性能与Q-MP类似，尽管后者在理论上是完整的，但在实践中不可扩展。在附录F中，我们进一步比较了SphereNet和其他模型在参数和时间成本方面的效率。SphereNet使用了与其他模型类似的计算预算，但实现了最佳性能。
表4:MD17上使用两个骨干网络的SMP和Q-MP之间的比较

消融研究
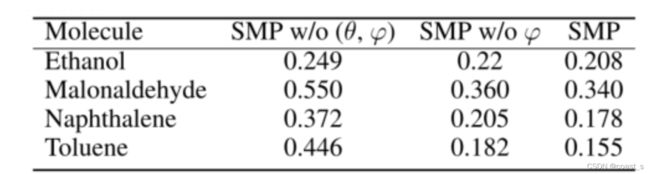
提出的SMP考虑了所有的距离、角度和扭转，从而产生了更强大的数据表示。我们研究了不同几何结构的贡献，以证明我们的SMP的进步。我们从SMP中去除扭转信息，我们称之为“SMP w/oφ”；我们进一步删除了我们称为“SMP w/o（θ，φ）”的角度信息。这三种消息传递策略集成到同一体系结构中，其他网络部分保持不变。我们在MD17的四个分子上评估了这些模型。表5显示，SMP优于SMP w/oφ，SMP w/oφ优于“SMP w/o（θ，φ）”。这些结果证明了SMP中使用的角度和扭转信息的有效性。SMP的最佳性能进一步表明，SMP代表了3D图形的精确方案。此外，我们在附录G中提供了SphereNet过滤器的可视化结果，以进一步表明所有距离、角度和扭转信息都决定了过滤器的结构语义。
表5：部分MD17数据集上相同SphereNet体系结构上三种消息传递策略的比较

结论：

3D信息对于分子是重要的，但是缺乏一个原则性的消息传递框架来考虑它。我们首先提出球形消息传递作为一种统一而有效的方案，可以在不增加计算预算的情况下实现分子的近似完整表示。基于SMP和有意义的物理表示，SphereNet被提出，在各种类型的数据集上的实验证明了它的能力、效率和可扩展性