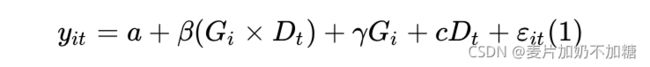使用 Python 计算 DID 及其对应P值
1. DID（Differences-in-Differences）定义
双重差分法，其主要被用于社会学中的政策效果评估。这种方法需要两个「差异」数据。一个是干预前后的「差异」，这个是自身实验前后的差异。另外一个是干预组与对照组的「差异」。DID利用这两个「差异」的差异来推算干预的效果。因此，顾名思义叫做双重差分法。
其原理是基于一个反事实的框架来评估政策发生和不发生这两种情况下被观测因素y的变化。如果一个外生的政策冲击将样本分为两组：受政策干预的Treat组和未受政策干预的Control组（在政策冲击前，Treat组和Control组的y没有显著差异）。那么，可以将Control组在政策发生前后y的变化看作Treat组未受政策冲击时的状况（反事实的结果）。通过比较Treat组y的变化(D1)以及Control组y的变化（D2），就可以得到政策冲击的实际效果(DD=D1-D2)。
注意：只有在满足“政策冲击前Treat组和Control组的y没有显著差异”（即平行性假定）的条件下，得到的双重差分估计量才是无偏的。
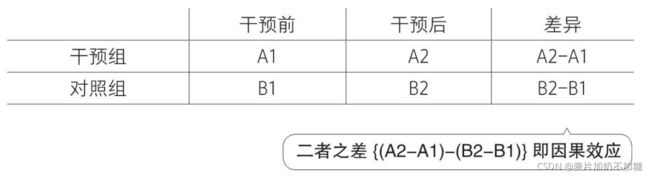
如下图所示：
干预组实验前为A1，实验后为A2。对照组实验前为B1，实验后为B2。对于干预组实验前后差异为A2-A1，对于对照组实验后为B2-B1。两者之差（A2-A1）-（B2-B1）即为DID结果，因果效应/处理效应。如下图处理效应所代表的部分。
2. DID模型形式
为分组虚拟变量（处理组=1，控制组=0）； 为分期虚拟变量（政策实施后=1，政策实施前=0）；交互项 表示处理组在政策实施后的效应，其系数即为双重差分模型重点考察的处理效应。
3. OLS多项式拟合
根据DID公式，我们可以通过使用多项式拟合的方法来求得DID及其P值。以下为Pyhton方法：使用statsmodels库中ols方法，需要根据上述公式准备数据，t代表时间（干预前=0，干预后=1）、g代表分组（干预组=1，对照组=0）、还有一个是交叉项tg（计算其t*g即可）。
代码如下：
import statsmodels.formula.api as smf
import pandas as pd
v1 =[0.367730,0.377147,0.352539,0.341864,0.29276,0.393443,0.374697,0.346989,0.385783,0.307801]
t1 = [0,0,0,0,1,0,0,0,0,1]
g1 =[1,1,1,1,1,0,0,0,0,0]
tg1 = [0,0,0,0,1,0,0,0,0,0]
aa = pd.DataFrame({'t1':t1,'g1':g1,'tg1':tg1,'v1':v1})
X = aa[['t1', 'g1','tg1']]
y = aa['v1']
est = smf.ols(formula='v1 ~ t1 + g1 + tg1', data=aa).fit()
y_pred = est.predict(X)
aa['v1_pred'] = y_pred
print(aa)
print(est.summary())
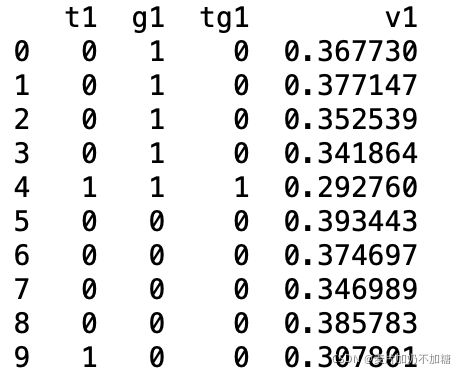
print(est.params) 准备数据格式如下：
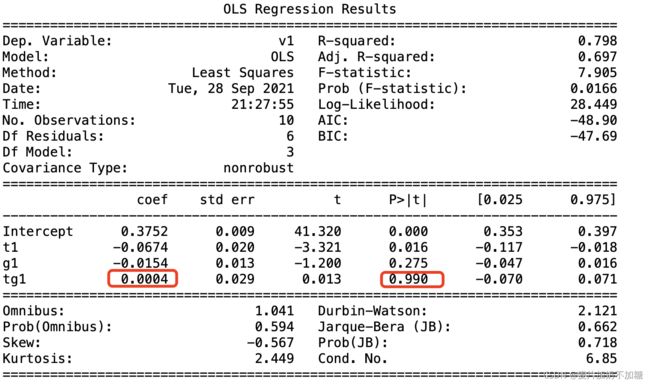
OLS结果Summary如下：
交叉项的系数就是DID结果，处理效应。P>| t |为其P值，小于0.05表示差异显著。
参考资料：
1. 双重差分法(DID)入门必看 - 知乎
2. 什么是双重差分模型（：difference-in-differences model）？ - 知乎
3. Python 普通最小二乘法（OLS）进行多项式拟合_公众号：SQLServer-CSDN博客