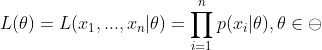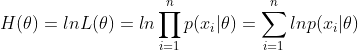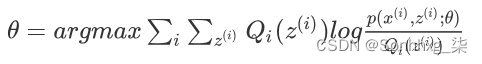【机器学习】最大期望算法(EM)

1. 什么是EM算法

最大期望算法（Expectation-maximization algorithm，又译为期望最大化算法），是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐性变量。

最大期望算法经过两个步骤交替进行计算，

第一步是计算期望（E），利用对隐藏变量的现有估计值，计算其最大似然估计值； 第二步是最大化（M），最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中，这个过程不断交替进行。

极大似然估计用一句话概括就是：知道结果，反推条件θ。

1.1 似然函数

在数理统计学中，似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。“似然性”与“或然性”或“概率”意思相近，都是指某种事件发生的可能性。而极大似然就相当于最大可能的意思。

比如你一位同学和一位猎人一起外出打猎，一只野兔从前方窜过。只听一声枪响，野兔应声到下，如果要你推测，这一发命中的子弹是谁打的？你就会想，只发一枪便打中，由于猎人命中的概率一般大于你那位同学命中的概率，从而推断出这一枪应该是猎人射中的。

这个例子所作的推断就体现了最大似然法的基本思想。

多数情况下我们是根据已知条件来推算结果，而最大似然估计是已经知道了结果，然后寻求使该结果出现的可能性最大的条件，以此作为估计值。

1.3 极大似然函数的求解步骤

假定我们要从10万个人当中抽取100个人来做身高统计，那么抽到这100个人的概率就是(概率连乘)：

 

现在要求的就是这个 值，也就是使得 的概率最大化，那么这时的参数 就是所求。

 

为了便于分析，我们可以定义对数似然函数，将其变成连加的形式：

 

对于求一个函数的极值，通过我们在本科所学的微积分知识，最直接的设想是求导，然后让导数为0，那么解这个方程得到的θ就是了（当然，前提是函数L(θ)连续可微）。但，如果θ是包含多个参数的向量那怎么处理呢？当然是求L(θ)对所有参数的偏导数，也就是梯度了，从而n个未知的参数，就有n个方程，方程组的解就是似然函数的极值点了，最终得到这n个参数的值。

求极大似然函数估计值的一般步骤：

1. 写出似然函数；
2. 对似然函数取对数，并整理；
3. 求导数，令导数为0，得到似然方程；
4. 解似然方程，得到的参数即为所求；

1.4 EM算法

两枚硬币A和B，假定随机抛掷后正面朝上概率分别为PA，PB。为了估计这两个硬币朝上的概率，咱们轮流抛硬币A和B，每一轮都连续抛5次，总共5轮：

硬币	结果	统计
A	正正反正反	3正-2反
B	反反正正反	2正-3反
A	正反反反反	1正-4反
B	正反反正正	3正-2反
A	反正正反反	2正-3反

硬币A被抛了15次，在第一轮、第三轮、第五轮分别出现了3次正、1次正、2次正，所以很容易估计出PA，类似的，PB也很容易计算出来(真实值)，如下：

PA = （3+1+2）/ 15 = 0.4 PB= （2+3）/10 = 0.5

问题来了，如果我们不知道抛的硬币是A还是B呢（即硬币种类是隐变量），然后再轮流抛五轮，得到如下结果：

硬币	结果	统计
Unknown	正正反正反	3正-2反
Unknown	反反正正反	2正-3反
Unknown	正反反反反	1正-4反
Unknown	正反反正正	3正-2反
Unknown	反正正反反	2正-3反

OK，问题变得有意思了。现在我们的目标没变，还是估计PA和PB，需要怎么做呢？

显然，此时我们多了一个硬币种类的隐变量，设为z，可以把它认为是一个5维的向量（z1,z2,z3,z4,z5)，代表每次投掷时所使用的硬币，比如z1，就代表第一轮投掷时使用的硬币是A还是B。

• 但是，这个变量z不知道，就无法去估计PA和PB，所以，我们必须先估计出z，然后才能进一步估计PA和PB。
• 可要估计z，我们又得知道PA和PB，这样我们才能用极大似然概率法则去估计z，这不是鸡生蛋和蛋生鸡的问题吗，如何破？

答案就是先随机初始化一个PA和PB，用它来估计z，然后基于z，还是按照最大似然概率法则去估计新的PA和PB，然后依次循环，如果新估计出来的PA和PB和我们真实值差别很大，直到PA和PB收敛到真实值为止。

我们不妨这样，先随便给PA和PB赋一个值，比如： 硬币A正面朝上的概率PA = 0.2 硬币B正面朝上的概率PB = 0.7

然后，我们看看第一轮抛掷最可能是哪个硬币。 如果是硬币A，得出3正2反的概率为 0.20.20.20.80.8 = 0.00512 如果是硬币B，得出3正2反的概率为0.70.70.70.30.3=0.03087 然后依次求出其他4轮中的相应概率。做成表格如下：

轮数	若是硬币A	若是硬币B
1	0.00512，即0.2 0.2 0.2 0.8 0.8，3正-2反	0.03087，3正-2反
2	0.02048，即0.2 0.2 0.8 0.8 0.8，2正-3反	0.01323，2正-3反
3	0.08192，即0.2 0.8 0.8 0.8 0.8，1正-4反	0.00567，1正-4反
4	0.00512，即0.2 0.2 0.2 0.8 0.8，3正-2反	0.03087，3正-2反
5	0.02048，即0.2 0.2 0.8 0.8 0.8，2正-3反	0.01323，2正-3反

按照最大似然法则： 第1轮中最有可能的是硬币B 第2轮中最有可能的是硬币A 第3轮中最有可能的是硬币A 第4轮中最有可能的是硬币B 第5轮中最有可能的是硬币A

我们就把概率更大，即更可能是A的，即第2轮、第3轮、第5轮出现正的次数2、1、2相加，除以A被抛的总次数15（A抛了三轮，每轮5次），作为z的估计值，B的计算方法类似。然后我们便可以按照最大似然概率法则来估计新的PA和PB。

PA = （2+1+2）/15 = 0.33 PB =（3+3）/10 = 0.6

就这样，不断迭代 不断接近真实值，这就是EM算法的奇妙之处。

可以期待，我们继续按照上面的思路，用估计出的PA和PB再来估计z，再用z来估计新的PA和PB，反复迭代下去，就可以最终得到PA = 0.4，PB=0.5，此时无论怎样迭代，PA和PB的值都会保持0.4和0.5不变，于是乎，我们就找到了PA和PB的最大似然估计。

总结一下计算步骤：

1. 随机初始化分布参数θ

2. E步，求Q函数，对于每一个i，计算根据上一次迭代的模型参数来计算出隐性变量的后验概率（其实就是隐性变量的期望），来作为隐藏变量的现估计值：

3. M步，求使Q函数获得极大时的参数取值）将似然函数最大化以获得新的参数值

4. 然后循环重复2、3步直到收敛。

详细的推导过程请参考文末的参考文献。

2. 采用 EM 算法求解的模型有哪些？

用EM算法求解的模型一般有GMM或者协同过滤，k-means其实也属于EM。EM算法一定会收敛，但是可能收敛到局部最优。由于求和的项数将随着隐变量的数目指数上升，会给梯度计算带来麻烦。

3.代码实现

gmm-em-clustering

高斯混合模型（GMM 聚类）的 EM 算法实现。

在给出代码前，先作一些说明。

• 在对样本应用高斯混合模型的 EM 算法前，需要先进行数据预处理，即把所有样本值都缩放到 0 和 1 之间。
• 初始化模型参数时，要确保任意两个模型之间参数没有完全相同，否则迭代到最后，两个模型的参数也将完全相同，相当于一个模型。
• 模型的个数必须大于 1。当 K 等于 1 时相当于将样本聚成一类，没有任何意义。

代码在main.py和gmm.py中

gmm.py

# -*- coding: utf-8 -*-
# ----------------------------------------------------
# Copyright (c) 2017, Wray Zheng. All Rights Reserved.
# Distributed under the BSD License.
# ----------------------------------------------------

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

DEBUG = True

######################################################
# 调试输出函数
# 由全局变量 DEBUG 控制输出
######################################################
def debug(*args, **kwargs):
    global DEBUG
    if DEBUG:
        print(*args, **kwargs)


######################################################
# 第 k 个模型的高斯分布密度函数
# 每 i 行表示第 i 个样本在各模型中的出现概率
# 返回一维列表
######################################################
def phi(Y, mu_k, cov_k):
    norm = multivariate_normal(mean=mu_k, cov=cov_k)
    return norm.pdf(Y)


######################################################
# E 步：计算每个模型对样本的响应度
# Y 为样本矩阵，每个样本一行，只有一个特征时为列向量
# mu 为均值多维数组，每行表示一个样本各个特征的均值
# cov 为协方差矩阵的数组，alpha 为模型响应度数组
######################################################
def getExpectation(Y, mu, cov, alpha):
    # 样本数
    N = Y.shape[0]
    # 模型数
    K = alpha.shape[0]

    # 为避免使用单个高斯模型或样本，导致返回结果的类型不一致
    # 因此要求样本数和模型个数必须大于1
    assert N > 1, "There must be more than one sample!"
    assert K > 1, "There must be more than one gaussian model!"

    # 响应度矩阵，行对应样本，列对应响应度
    gamma = np.mat(np.zeros((N, K)))

    # 计算各模型中所有样本出现的概率，行对应样本，列对应模型
    prob = np.zeros((N, K))
    for k in range(K):
        prob[:, k] = phi(Y, mu[k], cov[k])
    prob = np.mat(prob)

    # 计算每个模型对每个样本的响应度
    for k in range(K):
        gamma[:, k] = alpha[k] * prob[:, k]
    for i in range(N):
        gamma[i, :] /= np.sum(gamma[i, :])
    return gamma


######################################################
# M 步：迭代模型参数
# Y 为样本矩阵，gamma 为响应度矩阵
######################################################
def maximize(Y, gamma):
    # 样本数和特征数
    N, D = Y.shape
    # 模型数
    K = gamma.shape[1]

    #初始化参数值
    mu = np.zeros((K, D))
    cov = []
    alpha = np.zeros(K)

    # 更新每个模型的参数
    for k in range(K):
        # 第 k 个模型对所有样本的响应度之和
        Nk = np.sum(gamma[:, k])
        # 更新 mu
        # 对每个特征求均值
        for d in range(D):
            mu[k, d] = np.sum(np.multiply(gamma[:, k], Y[:, d])) / Nk
        # 更新 cov
        cov_k = np.mat(np.zeros((D, D)))
        for i in range(N):
            cov_k += gamma[i, k] * (Y[i] - mu[k]).T * (Y[i] - mu[k]) / Nk
        cov.append(cov_k)
        # 更新 alpha
        alpha[k] = Nk / N
    cov = np.array(cov)
    return mu, cov, alpha


######################################################
# 数据预处理
# 将所有数据都缩放到 0 和 1 之间
######################################################
def scale_data(Y):
    # 对每一维特征分别进行缩放
    for i in range(Y.shape[1]):
        max_ = Y[:, i].max()
        min_ = Y[:, i].min()
        Y[:, i] = (Y[:, i] - min_) / (max_ - min_)
    debug("Data scaled.")
    return Y


######################################################
# 初始化模型参数
# shape 是表示样本规模的二元组，(样本数, 特征数)
# K 表示模型个数
######################################################
def init_params(shape, K):
    N, D = shape
    mu = np.random.rand(K, D)
    cov = np.array([np.eye(D)] * K)
    alpha = np.array([1.0 / K] * K)
    debug("Parameters initialized.")
    debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")
    return mu, cov, alpha


######################################################
# 高斯混合模型 EM 算法
# 给定样本矩阵 Y，计算模型参数
# K 为模型个数
# times 为迭代次数
######################################################
def GMM_EM(Y, K, times):
    Y = scale_data(Y)
    mu, cov, alpha = init_params(Y.shape, K)
    for i in range(times):
        gamma = getExpectation(Y, mu, cov, alpha)
        mu, cov, alpha = maximize(Y, gamma)
    debug("{sep} Result {sep}".format(sep="-" * 20))
    debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")
    return mu, cov, alpha

main.py

 

# -*- coding: utf-8 -*-
# ----------------------------------------------------
# Copyright (c) 2017, Wray Zheng. All Rights Reserved.
# Distributed under the BSD License.
# ----------------------------------------------------

import matplotlib.pyplot as plt
from gmm import *

# 设置调试模式
DEBUG = True

# 载入数据
Y = np.loadtxt("gmm.data")
matY = np.matrix(Y, copy=True)

# 模型个数，即聚类的类别个数
K = 2

# 计算 GMM 模型参数
mu, cov, alpha = GMM_EM(matY, K, 100)

# 根据 GMM 模型，对样本数据进行聚类，一个模型对应一个类别
N = Y.shape[0]
# 求当前模型参数下，各模型对样本的响应度矩阵
gamma = getExpectation(matY, mu, cov, alpha)
# 对每个样本，求响应度最大的模型下标，作为其类别标识
category = gamma.argmax(axis=1).flatten().tolist()[0]
# 将每个样本放入对应类别的列表中
class1 = np.array([Y[i] for i in range(N) if category[i] == 0])
class2 = np.array([Y[i] for i in range(N) if category[i] == 1])

# 绘制聚类结果
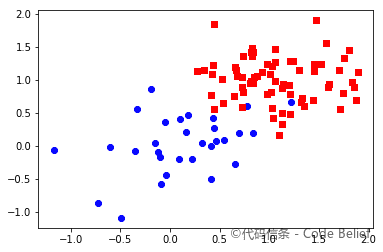
plt.plot(class1[:, 0], class1[:, 1], 'rs', label="class1")
plt.plot(class2[:, 0], class2[:, 1], 'bo', label="class2")
plt.legend(loc="best")
plt.title("GMM Clustering By EM Algorithm")
plt.show()

测试结果

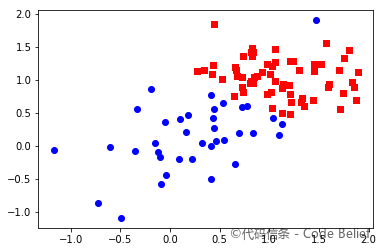
样本 1 原始类别：

样本 1 聚类结果：

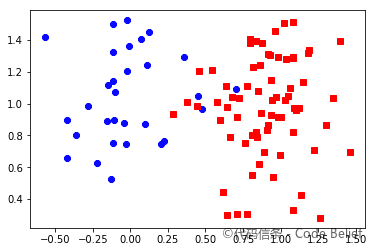
样本 2 原始类别：

样本 2 聚类结果：

测试数据

完整代码和数据放在了 Github 上，可 点此访问 。

或者通过下列代码生成测试数据：

import numpy as np
import matplotlib.pyplot as plt

cov1 = np.mat("0.3 0;0 0.1")
cov2 = np.mat("0.2 0;0 0.3")
mu1 = np.array([0, 1])
mu2 = np.array([2, 1])

sample = np.zeros((100, 2))
sample[:30, :] = np.random.multivariate_normal(mean=mu1, cov=cov1, size=30)
sample[30:, :] = np.random.multivariate_normal(mean=mu2, cov=cov2, size=70)
np.savetxt("sample.data", sample)

plt.plot(sample[:30, 0], sample[:30, 1], "bo")
plt.plot(sample[30:, 0], sample[30:, 1], "rs")
plt.show()