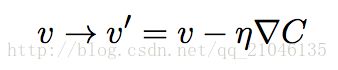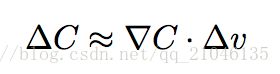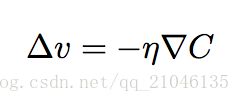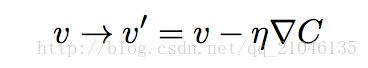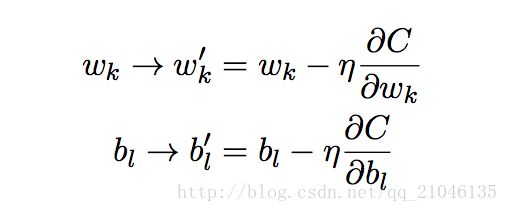神经网络与深度学习笔记(一)梯度下降算法
1、定义一个代价函数
w 表示所有的网络中权重的集合
n 是训练输入数据的个数
a 是表 示当输入为 x 时输出的向量
求和则是在总的训练输入 x 上进行的
C 称为二次代价函数;有时也称被称为均方误差或者 MSE
2、C
我们训练神经网络的目的是找到能最小化二次代价函数 C(w, b) 的权重和偏置
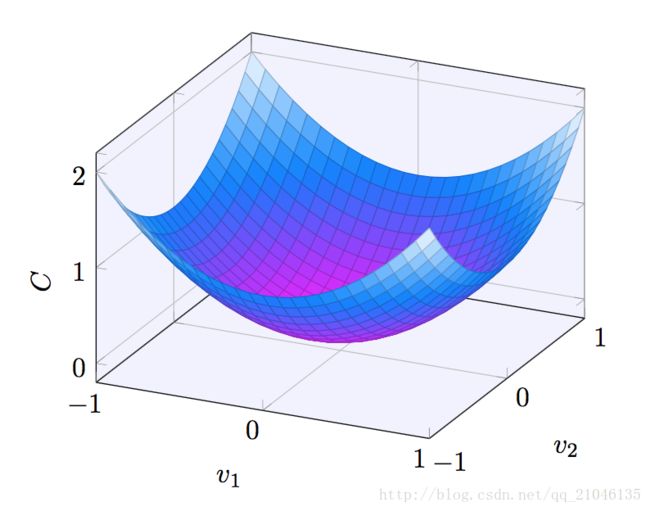
假设我们要最小化某些函数,C(v)。它可以是任意的多元实值函数,v = v1, v2, …。 注意我们用 v 代替了 w 和 b 以强调它可能是任意的函数 —— 我们现在先不局限于神经网络的环 境。为了最小化 C(v),想象 C 是一个只有两个变量 v1 和 v2 的函数:
3、为什么不能用微积分求最小值
我们可以计算导数去寻找 C 的极值点。 运气好的话,C 是一个只有一个或少数几个变量的函数。但是变量过多的话那就是噩梦。而且 神经网络中我们经常需要大量的变量——最大的神经网络有依赖数亿权重和偏置的代价函数,极 其复杂。用微积分来计算最小值已经不可行了。
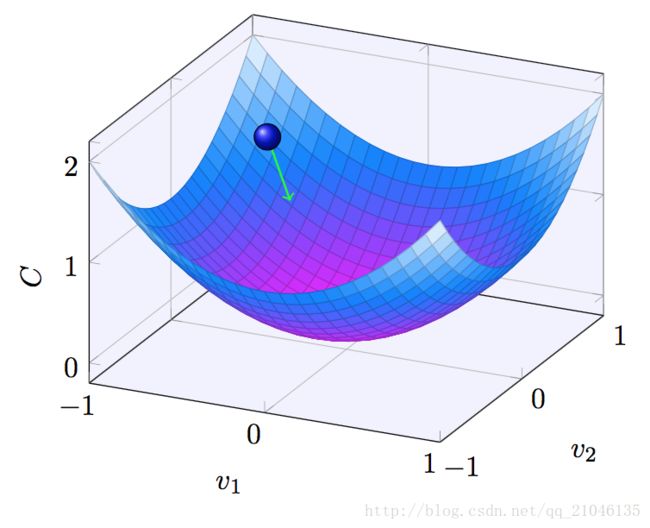
幸运的是,有一个漂亮的推导法暗示有一种算法能得到很好的效 果。首先把我们的函数想象成一个山谷。只要瞄一眼上面的绘图就不难理解。我们想象有一个 小球从山谷的斜坡滚落下来。我们的日常经验告诉我们这个球最终会滚到谷底。也许我们可以 用这一想法来找到函数的最小值?我们会为一个(假想的)球体随机选择一个起始位置,然后 模拟球体滚落到谷底的运动。我们可以通过计算 C 的导数(或者二阶导数)来简单模拟——这 些导数会告诉我们山谷中局部“形状”的一切,由此知道我们的球将怎样滚动。
4、C 的变化表示
v1 和 v2 方向分别将球体移动一个 很小的量,即 ∆v1 和 ∆v2 时
∆v 为 v 变化的向量:
∆v ≡ (∆v1, ∆v2)T
∇C 来表示梯度向量:
∆C 的表达式可以被重写为:
∇C 把 v 的变化关联为 C 的变化,正如我们 期望的用梯度来表示。但是这个方程真正让我们兴奋的是它让我们看到了如何选取 ∆v 才能让 ∆C 为负数。假设我们选取:
这里的 η 是个很小的正数(称为学习速率)。方程 (9) 告诉我们 ∆C ≈ −η∇C·∇C = −η∥∇C∥^2。 由于 ∥∇C∥^2 ≥ 0,这保证了 ∆C ≤ 0,即,如果我们按照方程的规则去改变 v,那么 C 会 一直减小,不会增加。
然后我们用它再次更新规则来计算下一次移动。如果我们反复持续这样做,我们将持续减小 C 直到 —— 正如我们希望的 —— 获得一个全局的最小值。
总结一下,梯度下降算法工作的方式就是重复计算梯度 ∇C,然后沿着相反的方向移动,沿 着山谷“滚落”。我们可以想象它像这样:
5、C 为多元情况下
C 是一个有 m 个变量 v1, … , vm 的多元函数。那么对 C 中自变量的变化 ∆v = (∆v1, … , ∆vm)T ,∆C 将会变为:
这里的梯度 ∇C 是向量:
正如两个变量的情况,我们可以选取:
而且 ∆C 的(近似)表达式 保证是负数。这给了我们一种方式从梯度中去取得最小值,
即使 C 是任意的多元函数,我们也能重复运用更新规则
我们无法从梯 度下降来求得函数 C 的全局最小值,但在实践中,梯 度下降算法通常工作地非常好,在神经网络中这是一种非常有效的方式去求代价函数的最小值, 进而促进网络自身的学习。
5、随即梯度下降
利用梯度下降算法去寻找能使 得方程的代价取得最小值的权重 wk 和偏置 bl。为了清楚这是如何工作的,我们将用权重和 偏置代替变量 vj。也就是说,现在“位置”变量有两个分量组成:wk 和 bl,而梯度向量 ∇C 则 有相应的分量 ∂C/∂wk 和 ∂C/∂bl。用这些分量来写梯度下降的更新规则,我们得到:
随机梯度下降的算法的思想就是通过随机选取小量训练输入样本来计算 ∇Cx,进而估算梯度 ∇C。通过计算少量样本的平均值我们可以快速得到一个对于实际梯度 ∇C 的很好的估算,这有助于加速梯度下降,进而加速学习过程。
随机梯度下降通过随机选取小量的 m 个训练输入来工作。我们将这些随机的
训练输入标记为 X1, X2, … , Xm,并把它们称为一个小批量数据(mini-batch)。假设样本数量 m 足够大,我们期望 ∇CXj 的平均值大致相等于整个 ∇Cx 的平均值,即,
则
假设 wk 和 bl 表示我们神经网络中权重和偏置。
随即梯度下降通过随机地选取并训练输入的小批量数据来工作,
可得