武汉大学惯性导航课程精要

市面上的传感器

基本上坐标轴都是固定的！坐标系都不可更改
mems误差都在5度每小时

week1

大地测量中有相关参考坐标系的内容。
卡尔曼滤波在组合导航中应用广泛。
开源代码的网站，需要多多注意

航位推算（Dead-Reckoning）

航位推算（Dead-Reckoning）
这是惯导的一个分类，经常和绝对测量结合起来，互补。正是我的freehand 项目所涉及的类型。

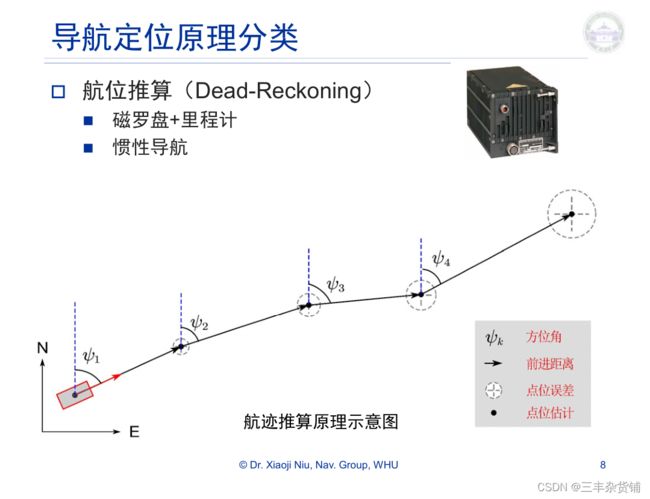
航位推算这里，淘宝店家基本没有测距离的，有一家，精度也很差，都是超过cm级的，cm级就算做得不错的了。

加速度计原理

PPT上说，测的是比力，就是f = a - g，默认减去重力加速度。
不过我自己买的传感器，默认情况下也是测量g的，不会减，而且相对各个轴是有正负的。是相对传感器上的惯性参考系吗？
我的传感器能不能初始化一个默认坐标系。产品默认的坐标是固定的，不能更改，这个坐标系又该怎么和超声波探头结合在一起？
MEMS加速度计精度不太行，比如传统的石英加速度计是有的更高。

陀螺仪

惯性参考系的角速率。
注意，这里是相对惯性参考系的，一个看不见摸不着的东西。
而类似编码器等，是测量一个物体转子相对于另一物体定子的角速率。

哥式效应，振动陀螺
想象陀螺，在运动的时候，会有一个轴，指向一直不变。所以传感器自身内部是有一个轴的。测量的是传感器相对于这个轴的转动角速度，最后能解算出角度。
我的传感器上，这个轴是不可以改变的。

惯性测量单元（IMU)

三轴加速度计 + 三轴陀螺仪
可以既感知角度！又感知线位移！
买来的传感器已经做好了误差等的标定。

INS

加上算法才是ins，才能输出位置，这个位置到底怎么确定？误差很大

week 2

惯性导航原理

1D

1D直接积分，加速度积分获得位置，角加速度积分获得角度。磁力计对z轴角度补偿。

3D

重点
由传感器数据获得载体相对于参考坐标系的方向及其变化的问题。
将传感器数据从“相对于惯性坐标系”转换到“相对于参考坐标系”。绝对的地球坐标系
需要补偿地球万有引力（重力）加速度。？？？这个需要补偿吗
平台式系统 和 捷联式系统 strapdown
(Gimbal vs. Strapdown)
捷联式系统现在更好用，全面胜出！！坐标通过角度做投影

买一个可以直接输出位置和角度的传感器，最好是捷联式的，依据计算，坐标投影，获得相对于初始坐标系的位置

误差

陀螺的误差是主要误差。
引入辅助信息，组合导航。
只有学过下面的导航分类，才知道，MEMS系统精度有的都可以达到战术级，零偏 4度/h，定位误差每小时竟然是千米，难怪我买的传感器RMS均方根误差是2mRMS，
现在的MEMS很多都能达到战术级，贵一点。

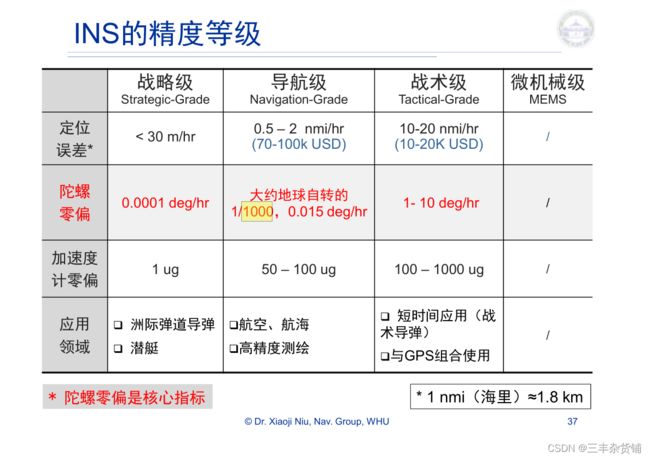
大概的误差估计可以用 误差（和真值差别） / 量程。

week3 误差和标定

理想输出

加速度 测的是比力：f = a - g，如果按照课件的轴摆放，输出竟然是-g。
陀螺仪输出的是w - 15度/h,
我的传感器，陀螺默认是0。

误差分类

week4 坐标系

1 ECM实用惯性坐标系

没有地球自转，室外导航经常用这个。

2 ECEF地心地固坐标系

3 导航坐标系（专有名词）

北东地
东北天
坐标系改变之后，所有公式都需要重新推

4 IMU坐标系（载体坐标系）

前右下
右前上，东北天的导航坐标系要选择这个IMU坐标系。
载体坐标系可能有很多个，因为有很多个传感器放在载体上，这些传感可能不能完美配合。

误差

imu传感器已经是调教好的，所以误差这里是不是不太用深究。

静态误差

噪声（noise）：白噪声，功率谱密度和单位略过。
温漂也是影响比较大的一个误差因素

week5

为什么加速度计的量程那么大。
传感器的输入信号带宽（不是输出的带宽）杀太低，rms小了。但是没有意义，带宽作为一个参数也需要考虑。
任何传感器，都希望输入的带宽足够高，足够大。
测量常值的时候，可以尽量杀带宽。

如上图，每次求平均值都是降低采样率的一种方式，可以减小看起来的噪声，不过看白噪声实质的那个值并没有减小。根据采样定理，它能感知的信号只有采样率的1/2，所以是杀带宽的方式。
在加速度的测量历史中，导弹的加速度给得越大越好，才能快速打击目标。所以量程设得很大，+-2000g这样就会有非线性误差，所以减小量程，会不会精度更高？角速度的量程要不要设置呢？

英语术语

Bias：是零位应该输入的值。模电不一样，数电就应该是0.
Bias error: 零偏误差
很多时候，bias和bias error都是零偏误差。
sf scale factor:

误差度量

随机误差，随机模型拟合
逐次上电重复性，每次上电都有陀螺零偏值，测了很多次，有正有负，因此，可以算：
rms：均方根， $\sigma$
P-P：给峰峰值 $6\sigma$
+/-：正最大值，负最大值 $3\sigma$
所以要传感器一般都标注rms，看起来好看。

week6

ALLan 方程，这里我略过了。只能看到主要矛盾，

案例分析：adis16488，2万块，0.5度/h，IIM42652， 2千块， 1.6度/ h,。

测试和标定

标定是为了补偿系统性误差，常值误差。

了获得准确的标定结果，需要一些专业设备（如
转台或规则的立方体）来获得IMU的精确姿态和旋
转角。
 由于对专业设备的依赖性，这些标定方法主要设计
用于实验室测试、厂家校准和对较高精度的IMU的
标定。

week7 INS的初始对准

买的那个传感器可以传位置，那个位置初始是怎么给的？变化过程中，位置相对原本坐标系变的吗？

位置必须给定
速度给定，或者为0
姿态的初始化最重要：粗对准和精对准。感觉这里是已经被做过了。

姿态本质上来讲，描述两个坐标系的角度关系。一个和和传感器一起运动的载体坐标系，另一个是自己选定的参考坐标系，一般是当地水平坐标系，比如北东地。姿态角yaw, pitch, rill只是表达的一种方式。

假设刚开始，两个坐标系完全对齐，认为参考坐标系经过三次旋转才到达相应的载体坐标系，先转航向，再俯仰，最后横滚，按照这个顺序~每个旋转都有正负方向。严格顺序，严格正负，那么这样严格定义的姿态角，没有歧义。

比如使用前右下和北东地的载体。与使用右前上和东北天的载体，经过这样严格的姿态定义，都可以到达相同的位置？

静态粗对准，静基座粗对准

这些对准，校准的方法，传感器有相关的教程。这里学一些理论：
感觉这里还是有必要学习的，不然买回来传感器以后，校准啥的操作也不会了。
这个对准就是在刚上电的时候，找到三个角的初始值？

加速度计调平，水瓶：

陀螺调整航向角：

静态解析粗对准-双矢量定姿：

week8

INS机械编排框图

姿态投影矩阵 是姿态的一种表达形式，把加速度投影到导航坐标系，才能积分。
实际算法很难~复杂：补偿，哥式，忽略，不考虑地球自传？ 忽略很多东西，就可以简化算法。传感器如果精度高些，那解算不能偷懒。

使用

使用

在使用惯导系统做测量应用之前
1.认真阅读设备使用手册
2.测试标定惯导系统, 估计出加速度计和陀螺仪的零偏和比例因子误差的确定性部分，并加以补偿
3.采集长时间的设备数据, 用来估计加速度计和陀螺的随机误差特性(例如，白噪声、零偏的一阶Gauss-Markov过程参数)
4.根据陀螺的噪声参数（ARW）估算所需初始对准的时长（考虑现实可行性）, 以保证初始对准的航向角精度
 做动态测试来演练并考核系统性能
1.验证导航算法实现的正确性, 精调算法参数, 预估辅助信息更新所需要的频率来保障一定的测量精度.
2.需要一个好的参考轨迹 (参考真值，通常是 GPS).
3.测试轨迹通常是富含典型动态信息的“L”或“S”形轨迹.

测试

定期零速修正或者坐标修正

使用的时候，一开始需要初始对准吗？这个看手册吧。

结束的时候，再采一下数据，和最初的状态做对比。可以分析一下问题，

事后处理

滤波算法
反向平滑
曲线，轨迹，检查正确性。qtchart，还是用ide界面。

以下是第2部分。

week 9 惯导算法

事后处理，反向平滑，一定要做，位置的发散可以很好地处理。
i系是惯性系。

预备知识

我们所要测量的量：
位置：载体相对于i系的位置
速度：地速是指载体相对地面的速度，不关心它在宇宙空间的速度。
姿态：b系相对于n系或者e系。姿态不是向量，不能用

向量是唯一的，在不同坐标系的三轴坐标是不同的。

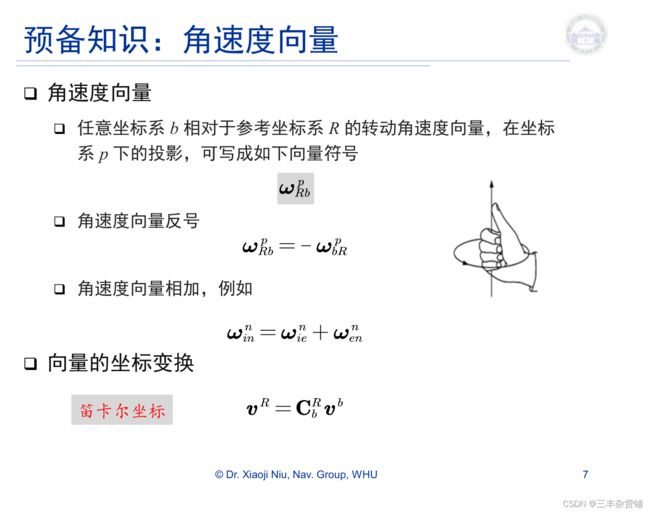
角速度是向量，所以可以叠加。姿态不能按叠加处理。都要投影到相同的坐标系比如n系。
这里可以知道，我们现在得到的姿态和位置都是针对某一个坐标系的。我需要把我项目中的这个坐标，转移到我想要的三维体的坐标中。然后通过3轴的投影，把这个图片的值，投影过去。这里我应该使用一些三维的切片，模拟一下算法。

如果一个三维向量想用3维矩阵表示，就写成反对称矩阵来表示，是构造出来的。这个东西很有用。是一个东西
反对称矩阵也可以做投影。

做积分的时候，采样率提高，有点用。工程上至少要比运动物体的带宽大5~10倍。我的运动物体运动很慢，带宽应该不是很高吧？

如果imu输出的是imu的位置增量输出，那就不用积分了，输出的就是直接的面积。

姿态结算考虑圆锥效应

姿态解算

不考虑平移
姿态的作用是投影变换，向量投影。

注意3个姿态角，一定不能交换。是按照指定角度旋转的。
规定俯仰角规定只有 ±90度，如果超过正负90度，我们就认为它的航向角180度旋转，横滚角也做180度的旋转。这是为了保证同一个姿态，只有一种欧拉角的表示方法。
俯仰角物理上变化一点角度，结果角度表示会有很大的变化。
(0, +89, 0) 俯仰再转2度—> (0, 91, 0) ----> (+180, 89, +180)

week10

姿态表示

方向余弦矩阵

三维的坐标变换矩阵，其实是三个二维的坐标转换矩阵连乘出来的。

这里绕y轴的坐标转换，没太理解。哈哈

+-90度出现奇点，那我的项目在做导航的时候，要注意角度？

姿态角一般用于输入输出，初始化，做姿态显示。但是姿态更新要用其他方法。

姿态投影矩阵为什么是方向余弦矩阵,因为它的每个元素都是两个基向量的方向余弦

坐标投影矩阵
看推导的物理意义。
方向余弦矩阵可以连乘

姿态投影矩阵的元素怎么求，就用欧拉角？
感觉可以用变化量的变化，来求上下两个角度投影矩阵。这里用到反对称阵。
姿态角的变化量，可以假设为小角度，简化欧拉角，不过我的项目不需要即时处理，应该可以用原本的矩阵吧

用处

1. 更新姿态：这里的推导很有意思。求解微分方程来求解

我的项目：其实有两种做法，1. 把初始的位置当作初始坐标系，在运动过程中，每几白毫秒会改变一个欧拉角的小量，那么就可以有一个转换矩阵转过去，如果位置也是相对于初始值的那就好了。 2. 就按照R系，可能是东北天坐标系，运动过程中的每一秒都在r系，最后把位置也建在r系中，这样就不用坐标转换了。投影到另一个坐标系

week11

解微分方程

dcm（方向余弦矩阵）和角加速度解方程，来求姿态。更新姿态
这里我略过了。感觉就是利用极限，求出角度和角速度的对应方程，然后知道角速度，求出角度。
微分方程这里还不太明白。

week12 - 四元数

也有基于姿态四元数的微分方程，也可以求解姿态。
可以认为是四维空间中的一个向量，可以表示四维空间中具有3个自由度的姿态。
复数形式，可以用两元表示二维空间中具有一个自由度的姿态

四元数的运算法则

四元数乘法不满足交换律。
四元数共轭（对应矩阵 转置），逆，及其运算。

最重要的是，把一个归一化的四元数，写成了角度的形式。使得一个向量可以绕另一个向量转$\thate$角度

四元数用一次转动表示三次连续转动。

由参考系转动到b系，转轴u，转角theta

坐标系变换投影的时候，四元数的计算量更大，要乘两次，所以方向余弦矩阵胜出。实际做向量投影，使用方向余弦矩阵做。

微分方程的求解

求解的时候，也有定轴旋转的假设。
如何弥补误差：
1.

week13 定轴旋转矢量